|
Mutual Coherence (linear Algebra)
In linear algebra, mutual coherence (or simply coherence) measures the maximum similarity between any two columns of a matrix, defined as the largest absolute value of their cross-correlations. First explored by David Donoho and Xiaoming Huo in the late 1990s for pairs of orthogonal bases, it was later expanded by Donoho and Michael Elad in the early 2000s to study sparse representations—where signals are built from a few key components in a larger set. In signal processing, mutual coherence is widely used to assess how well algorithms like matching pursuit and basis pursuit can recover a signal’s sparse representation from a collection with extra building blocks, known as an overcomplete dictionary. Joel Tropp extended this idea with the Babel function, which applies coherence from one column to a group, equaling mutual coherence for two columns while broadening its use for larger sets with any number of columns. Formal definition Formally, let a_1, \ldots, a_m\in ^d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Linear Algebra
Linear algebra is the branch of mathematics concerning linear equations such as :a_1x_1+\cdots +a_nx_n=b, linear maps such as :(x_1, \ldots, x_n) \mapsto a_1x_1+\cdots +a_nx_n, and their representations in vector spaces and through matrix (mathematics), matrices. Linear algebra is central to almost all areas of mathematics. For instance, linear algebra is fundamental in modern presentations of geometry, including for defining basic objects such as line (geometry), lines, plane (geometry), planes and rotation (mathematics), rotations. Also, functional analysis, a branch of mathematical analysis, may be viewed as the application of linear algebra to Space of functions, function spaces. Linear algebra is also used in most sciences and fields of engineering because it allows mathematical model, modeling many natural phenomena, and computing efficiently with such models. For nonlinear systems, which cannot be modeled with linear algebra, it is often used for dealing with first-order a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Cross-correlation
In signal processing, cross-correlation is a measure of similarity of two series as a function of the displacement of one relative to the other. This is also known as a ''sliding dot product'' or ''sliding inner-product''. It is commonly used for searching a long signal for a shorter, known feature. It has applications in pattern recognition, single particle analysis, electron tomography, averaging, cryptanalysis, and neurophysiology. The cross-correlation is similar in nature to the convolution of two functions. In an autocorrelation, which is the cross-correlation of a signal with itself, there will always be a peak at a lag of zero, and its size will be the signal energy. In probability and statistics, the term ''cross-correlations'' refers to the correlations between the entries of two random vectors \mathbf and \mathbf, while the ''correlations'' of a random vector \mathbf are the correlations between the entries of \mathbf itself, those forming the correlation mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Sparse Representation
Sparse is a computer software tool designed to find possible coding faults in the Linux kernel. Unlike other such tools, this static analysis tool was initially designed to only flag constructs that were likely to be of interest to kernel developers, such as the mixing of pointers to user and kernel address spaces. Sparse checks for known problems and allows the developer to include annotations in the code that convey information about data types, such as the address space that pointers point to and the locks that a function acquires or releases. Linus Torvalds started writing Sparse in 2003. Josh Triplett was its maintainer from 2006, a role taken over by Christopher Li in 2009 and by Luc Van Oostenryck in November 2018. Sparse is released under the MIT License. Annotations Some of the checks performed by Sparse require annotating the source code using the __attribute__ GCC extension, or the Sparse-specific __context__ specifier. Sparse defines the following list of attribu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
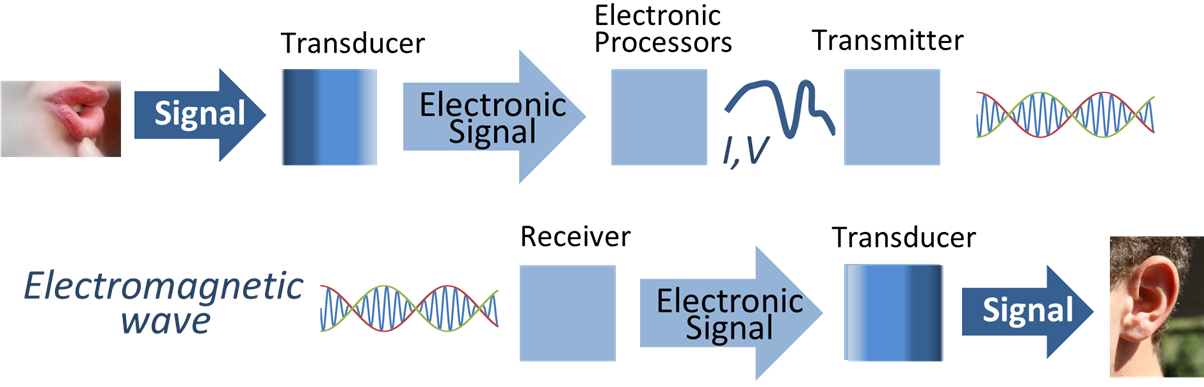
Signal Processing
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing ''signals'', such as audio signal processing, sound, image processing, images, Scalar potential, potential fields, Seismic tomography, seismic signals, Altimeter, altimetry processing, and scientific measurements. Signal processing techniques are used to optimize transmissions, Data storage, digital storage efficiency, correcting distorted signals, improve subjective video quality, and to detect or pinpoint components of interest in a measured signal. History According to Alan V. Oppenheim and Ronald W. Schafer, the principles of signal processing can be found in the classical numerical analysis techniques of the 17th century. They further state that the digital refinement of these techniques can be found in the digital control systems of the 1940s and 1950s. In 1948, Claude Shannon wrote the influential paper "A Mathematical Theory of Communication" which was publis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
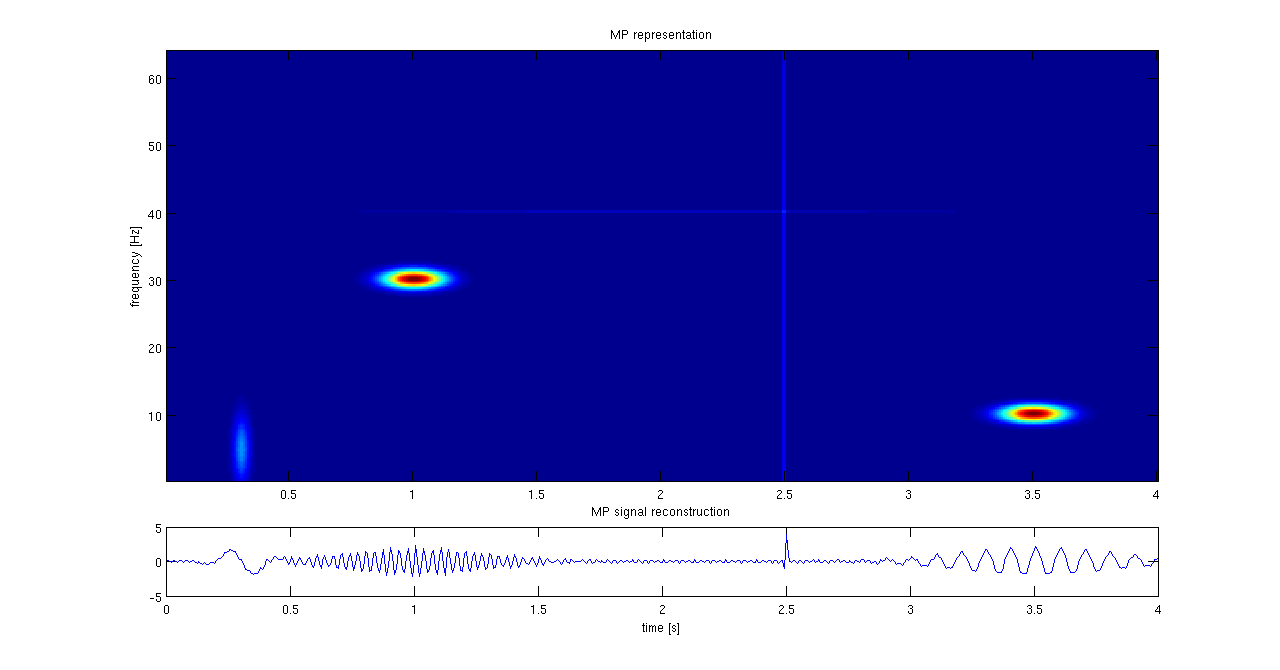
Matching Pursuit
Matching pursuit (MP) is a sparse approximation algorithm which finds the "best matching" projections of multidimensional data onto the span of an over-complete (i.e., redundant) dictionary D. The basic idea is to approximately represent a signal f from Hilbert space H as a weighted sum of finitely many functions g_ (called atoms) taken from D. An approximation with N atoms has the form : f(t) \approx \hat f_N(t) := \sum_^ a_n g_(t) where g_ is the \gamma_nth column of the matrix D and a_n is the scalar weighting factor (amplitude) for the atom g_. Normally, not every atom in D will be used in this sum. Instead, matching pursuit chooses the atoms one at a time in order to maximally (greedily) reduce the approximation error. This is achieved by finding the atom that has the highest inner product with the signal (assuming the atoms are normalized), subtracting from the signal an approximation that uses only that one atom, and repeating the process until the signal is satisfactoril ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Basis Pursuit
Basis pursuit is the mathematical optimization problem of the form : \min_x \, x\, _1 \quad \text \quad y = Ax, where ''x'' is a ''N''-dimensional solution vector (signal), ''y'' is a ''M''-dimensional vector of observations (measurements), ''A'' is a ''M'' × ''N'' transform matrix (usually measurement matrix) and ''M'' < ''N''. The version of basis pursuit that seeks to minimize the ''L''0 norm is NP-hard. It is usually applied in cases where there is an of linear equations ''y'' = ''Ax'' that must be exactly satisfied, and the sparsest solution in the ''L''1 sense is desired. When it is desirable to trade off exact equality of ''Ax'' and ''y'' in exchange for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Babel Function
In signal processing and mathematics, the Babel function, also known as cumulative coherence function (CCF), measures the maximum combined similarity between one fixed building block (called an ''atom'') and a group of other building blocks within a collection (called a ''dictionary''). Introduced by Joel Tropp as an extension of mutual coherence—which compares similarity between pairs of dictionary columns—the Babel function broadens this idea to assess how one column relates to multiple others at once, making it a key tool for analyzing sparse representations of signals. It applies to scenarios where signals can be efficiently described using a redundant dictionary matrix, a set of overlapping components used in areas like audio processing and data compression. Definition and formulation The Babel function of a dictionary \boldsymbol with normalized columns is a real-valued function that is defined as ::\mu_1(p) = \max_ \ where \boldsymbol_k are the columns (atoms) of the d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Compressed Sensing
Compressed sensing (also known as compressive sensing, compressive sampling, or sparse sampling) is a signal processing technique for efficiently acquiring and reconstructing a Signal (electronics), signal by finding solutions to Underdetermined system, underdetermined linear systems. This is based on the principle that, through optimization, the sparsity of a signal can be exploited to recover it from far fewer samples than required by the Nyquist–Shannon sampling theorem. There are two conditions under which recovery is possible. The first one is sparsity, which requires the signal to be sparse in some domain. The second one is incoherence, which is applied through the isometric property, which is sufficient for sparse signals. Compressed sensing has applications in, for example, magnetic resonance imaging (MRI) where the incoherence condition is typically satisfied. Overview A common goal of the engineering field of signal processing is to reconstruct a signal from a series ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Restricted Isometry Property
In linear algebra, the restricted isometry property (RIP) characterizes matrices which are nearly orthonormal, at least when operating on sparse vectors. The concept was introduced by Emmanuel Candès and Terence TaoE. J. Candes and T. Tao, "Decoding by Linear Programming," IEEE Trans. Inf. Th., 51(12): 4203–4215 (2005). and is used to prove many theorems in the field of compressed sensing. There are no known large matrices with bounded restricted isometry constants (computing these constants is strongly NP-hard, and is hard to approximate as well), but many random matrices have been shown to remain bounded. In particular, it has been shown that with exponentially high probability, random Gaussian, Bernoulli, and partial Fourier matrices satisfy the RIP with number of measurements nearly linear in the sparsity level. The current smallest upper bounds for any large rectangular matrices are for those of Gaussian matrices. Web forms to evaluate bounds for the Gaussian ensemble ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Signal Processing
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing ''signals'', such as audio signal processing, sound, image processing, images, Scalar potential, potential fields, Seismic tomography, seismic signals, Altimeter, altimetry processing, and scientific measurements. Signal processing techniques are used to optimize transmissions, Data storage, digital storage efficiency, correcting distorted signals, improve subjective video quality, and to detect or pinpoint components of interest in a measured signal. History According to Alan V. Oppenheim and Ronald W. Schafer, the principles of signal processing can be found in the classical numerical analysis techniques of the 17th century. They further state that the digital refinement of these techniques can be found in the digital control systems of the 1940s and 1950s. In 1948, Claude Shannon wrote the influential paper "A Mathematical Theory of Communication" which was publis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |