|
Mutual Coherence (linear Algebra)
In linear algebra, the coherence or mutual coherence of a matrix ''A'' is defined as the maximum absolute value of the cross-correlations between the columns of ''A''. Formally, let a_1, \ldots, a_m\in ^d be the columns of the matrix ''A'', which are assumed to be normalized such that a_i^H a_i = 1. The mutual coherence of ''A'' is then defined as :M = \max_ \left, a_i^H a_j \. A lower bound is : M\ge \sqrt A deterministic matrix with the mutual coherence almost meeting the lower bound can be constructed by Weil's theorem. This concept was reintroduced by David Donoho and Michael Elad in the context of sparse representations. A special case of this definition for the two-ortho case appeared earlier in the paper by Donoho and Huo. The mutual coherence has since been used extensively in the field of sparse representations of signals. In particular, it is used as a measure of the ability of suboptimal algorithms such as matching pursuit and basis pursuit to correctly identify ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Algebra
Linear algebra is the branch of mathematics concerning linear equations such as: :a_1x_1+\cdots +a_nx_n=b, linear maps such as: :(x_1, \ldots, x_n) \mapsto a_1x_1+\cdots +a_nx_n, and their representations in vector spaces and through matrices. Linear algebra is central to almost all areas of mathematics. For instance, linear algebra is fundamental in modern presentations of geometry, including for defining basic objects such as lines, planes and rotations. Also, functional analysis, a branch of mathematical analysis, may be viewed as the application of linear algebra to spaces of functions. Linear algebra is also used in most sciences and fields of engineering, because it allows modeling many natural phenomena, and computing efficiently with such models. For nonlinear systems, which cannot be modeled with linear algebra, it is often used for dealing with first-order approximations, using the fact that the differential of a multivariate function at a point is the line ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix (mathematics)
In mathematics, a matrix (plural matrices) is a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns, which is used to represent a mathematical object or a property of such an object. For example, \begin1 & 9 & -13 \\20 & 5 & -6 \end is a matrix with two rows and three columns. This is often referred to as a "two by three matrix", a "-matrix", or a matrix of dimension . Without further specifications, matrices represent linear maps, and allow explicit computations in linear algebra. Therefore, the study of matrices is a large part of linear algebra, and most properties and operations of abstract linear algebra can be expressed in terms of matrices. For example, matrix multiplication represents composition of linear maps. Not all matrices are related to linear algebra. This is, in particular, the case in graph theory, of incidence matrices, and adjacency matrices. ''This article focuses on matrices related to linear algebra, an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cross-correlation
In signal processing, cross-correlation is a measure of similarity of two series as a function of the displacement of one relative to the other. This is also known as a ''sliding dot product'' or ''sliding inner-product''. It is commonly used for searching a long signal for a shorter, known feature. It has applications in pattern recognition, single particle analysis, electron tomography, averaging, cryptanalysis, and neurophysiology. The cross-correlation is similar in nature to the convolution of two functions. In an autocorrelation, which is the cross-correlation of a signal with itself, there will always be a peak at a lag of zero, and its size will be the signal energy. In probability and statistics, the term ''cross-correlations'' refers to the correlations between the entries of two random vectors \mathbf and \mathbf, while the ''correlations'' of a random vector \mathbf are the correlations between the entries of \mathbf itself, those forming the correlation mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
David Donoho
David Leigh Donoho (born March 5, 1957) is an American statistician. He is a professor of statistics at Stanford University, where he is also the Anne T. and Robert M. Bass Professor in the Humanities and Sciences. His work includes the development of effective methods for the construction of low-dimensional representations for high-dimensional data problems (multiscale geometric analysis), development of wavelets for denoising and compressed sensing. He was elected a Member of the American Philosophical Society in 2019. Academic biography Donoho did his undergraduate studies at Princeton University, graduating in 1978. His undergraduate thesis advisor was John W. Tukey. Donoho obtained his Ph.D. from Harvard University in 1983, under the supervision of Peter J. Huber.. He was on the faculty of the University of California, Berkeley, from 1984 to 1990 before moving to Stanford. He has been the Ph.D. advisor of at least 20 doctoral students, including Jianqing Fan and Emman ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Michael Elad
Michael Elad (born December 10, 1963) is a professor of Computer Science at the Technion - Israel Institute of Technology. His work includes fundamental contributions in the field of sparse representations, and deployment of these ideas to algorithms and applications in signal processing, image processing and machine learning. Academic career Elad holds a B.Sc. (1986), M.Sc. (1988) and D.Sc. (1997) in electrical engineering from the Technion - Israel Institute of Technology. His M.Sc., under the guidance of Prof. David Malah, focused on video compression algorithms; and his D.Sc. on super-resolution algorithms for image sequences, guided by Prof. Arie Feuer. After several years (1997–2001) in industrial research in Hewlett-Packard Lab Israel and in Jigami, Michael took a research associate position at Stanford University from 2001 to 2003, working closely with Prof. Gene Golub (CS-Stanford), Prof. Peyman Milanfar (EE- UCSC) and Prof. David L. Donoho (Statistics-Stanford). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sparse Approximation
Sparse approximation (also known as sparse representation) theory deals with sparse solutions for systems of linear equations. Techniques for finding these solutions and exploiting them in applications have found wide use in image processing, signal processing, machine learning, medical imaging, and more. Sparse decomposition Noiseless observations Consider a linear system of equations x = D\alpha, where D is an underdetermined m\times p matrix (m < p) and . The matrix (typically assumed to be full-rank) is referred to as the dictionary, and is a signal of interest. The core sparse representation problem is defined as the quest for the sparsest possible representation satisfying . Due to the underdetermined nature of , this linear system admits in general infinitely many possible solutions, and among these we seek the one with the few ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Signal (electrical Engineering)
In signal processing, a signal is a function that conveys information about a phenomenon. Any quantity that can vary over space or time can be used as a signal to share messages between observers. The '' IEEE Transactions on Signal Processing'' includes audio, video, speech, image, sonar, and radar as examples of signal. A signal may also be defined as observable change in a quantity over space or time (a time series), even if it does not carry information. In nature, signals can be actions done by an organism to alert other organisms, ranging from the release of plant chemicals to warn nearby plants of a predator, to sounds or motions made by animals to alert other animals of food. Signaling occurs in all organisms even at cellular levels, with cell signaling. Signaling theory, in evolutionary biology, proposes that a substantial driver for evolution is the ability of animals to communicate with each other by developing ways of signaling. In human engineering, signals are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
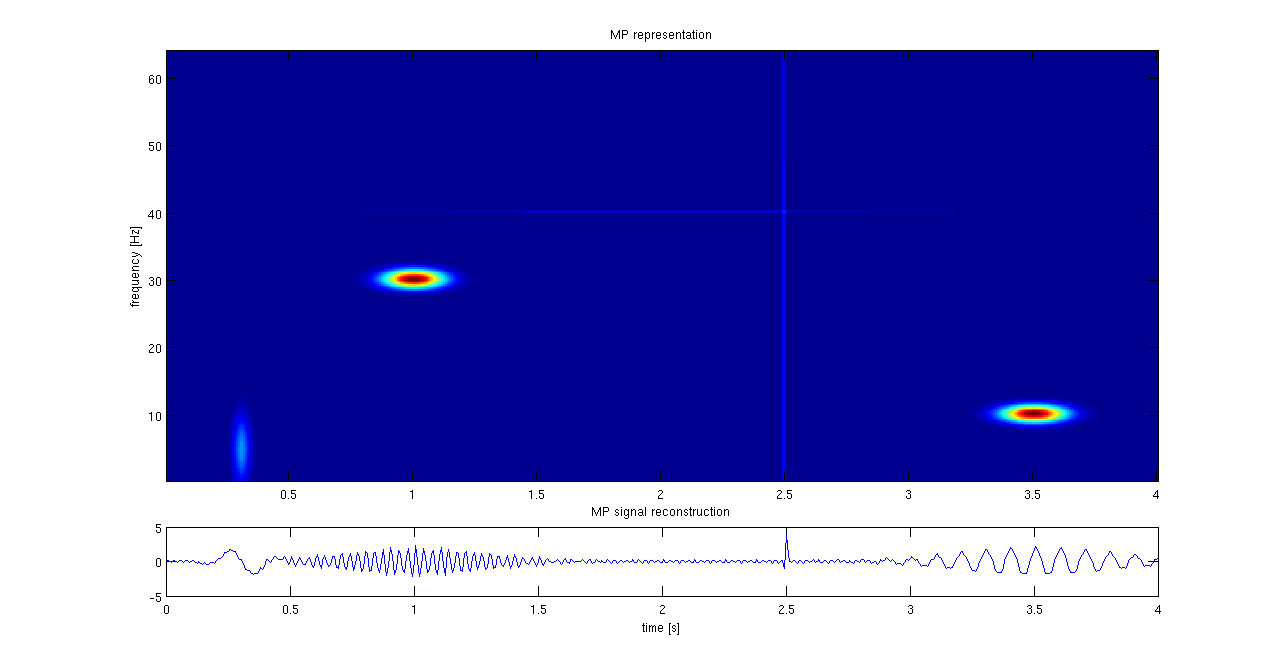
Matching Pursuit
Matching pursuit (MP) is a sparse approximation algorithm which finds the "best matching" projections of multidimensional data onto the span of an over-complete (i.e., redundant) dictionary D. The basic idea is to approximately represent a signal f from Hilbert space H as a weighted sum of finitely many functions g_ (called atoms) taken from D. An approximation with N atoms has the form : f(t) \approx \hat f_N(t) := \sum_^ a_n g_(t) where g_ is the \gamma_nth column of the matrix D and a_n is the scalar weighting factor (amplitude) for the atom g_. Normally, not every atom in D will be used in this sum. Instead, matching pursuit chooses the atoms one at a time in order to maximally (greedily) reduce the approximation error. This is achieved by finding the atom that has the highest inner product with the signal (assuming the atoms are normalized), subtracting from the signal an approximation that uses only that one atom, and repeating the process until the signal is satisfactorily d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Basis Pursuit
Basis pursuit is the mathematical optimization problem of the form : \min_x \, x\, _1 \quad \text \quad y = Ax, where ''x'' is a ''N''-dimensional solution vector (signal), ''y'' is a ''M''-dimensional vector of observations (measurements), ''A'' is a ''M'' × ''N'' transform matrix (usually measurement matrix) and ''M'' < ''N''. It is usually applied in cases where there is an underdetermined system of linear equations ''y'' = ''Ax'' that must be exactly satisfied, and the sparsest solution in the ''L''1 sense is desired. When it is desirable to trade off exact equality of ''Ax'' and ''y'' in exchange for a sparser ''x'', is preferred. Basis pursuit problems can be converted to [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Babel Function
The Babel function (also known as cumulative coherence) measures the maximum total coherence between a fixed atom and a collection of other atoms in a dictionary. The Babel function was conceived of in the context of signals for which there exists a sparse representation consisting of atoms or columns of a redundant dictionary matrix, A. Definition and formulation The Babel function of a dictionary \boldsymbol with normalized columns is a real-valued function that is defined as ::\mu_1(p) = \max_ \ where \boldsymbol_k are the columns (atoms) of the dictionary \boldsymbol . Special case When p=1, the babel function is the mutual coherence. Practical Applications Li and Lin have used the Babel function to aid in creating effective dictionaries for Machine Learning applications. References {{reflist See also * Compressed sensing Compressed sensing (also known as compressive sensing, compressive sampling, or sparse sampling) is a signal processing technique for efficiently a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compressed Sensing
Compressed sensing (also known as compressive sensing, compressive sampling, or sparse sampling) is a signal processing technique for efficiently acquiring and reconstructing a signal, by finding solutions to underdetermined linear systems. This is based on the principle that, through optimization, the sparsity of a signal can be exploited to recover it from far fewer samples than required by the Nyquist–Shannon sampling theorem. There are two conditions under which recovery is possible. The first one is sparsity, which requires the signal to be sparse in some domain. The second one is incoherence, which is applied through the isometric property, which is sufficient for sparse signals. Overview A common goal of the engineering field of signal processing is to reconstruct a signal from a series of sampling measurements. In general, this task is impossible because there is no way to reconstruct a signal during the times that the signal is not measured. Nevertheless, with prior ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |