|
Monotonicity (mechanism Design)
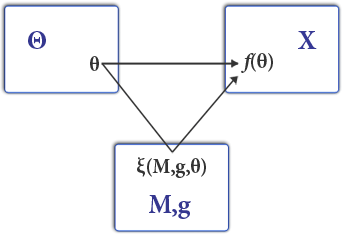
In mechanism design, monotonicity is a property of a social choice function. It is a necessary condition for being able to implement such a function using a strategyproof mechanism. Its verbal description is: In other words: Notation There is a set X of possible outcomes. There are n agents which have different valuations for each outcome. The valuation of agent i is represented as a function:v_i : X \longrightarrow R_+which expresses the value it assigns to each alternative. The vector of all value-functions is denoted by v. For every agent i, the vector of all value-functions of the ''other'' agents is denoted by v_. So v \equiv (v_i,v_). A social choice function is a function that takes as input the value-vector v and returns an outcome x\in X. It is denoted by \text(v) or \text(v_i,v_). In mechanisms without money A social choice function satisfies the strong monotonicity property (SMON) if for every agent i and every v_i,v_i',v_, if:x = \text(v_i, v_)x' = \text(v' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mechanism Design
Mechanism design (sometimes implementation theory or institution design) is a branch of economics and game theory. It studies how to construct rules—called Game form, mechanisms or institutions—that produce good outcomes according to Social welfare function, some predefined metric, even when the designer does not know the players' true preferences or what information they have. Mechanism design thus focuses on the study of solution concepts for a class of private-information games. Mechanism design has broad applications, including traditional domains of economics such as market design, but also political science (through voting theory). It is a foundational component in the operation of the internet, being used in networked systems (such as inter-domain routing), e-commerce, and Sponsored search auction, advertisement auctions by Facebook and Google. Because it starts with the end of the game (a particular result), then works backwards to find a game that implements it, it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Social Choice Function
In welfare economics and social choice theory, a social welfare function—also called a social ordering, ranking, utility, or choice function—is a function that ranks a set of social states by their desirability. Each person's preferences are combined in some way to determine which outcome is considered better by society as a whole. It can be seen as mathematically formalizing Rousseau's idea of a general will. Social choice functions are studied by economists as a way to identify socially-optimal decisions, giving a procedure to rigorously define which of two outcomes should be considered better for society as a whole (e.g. to compare two different possible income distributions). They are also used by democratic governments to choose between several options in elections, based on the preferences of voters; in this context, a social choice function is typically referred to as an electoral system. The notion of social utility is analogous to the notion of a utility fun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Strategyproof
In mechanism design, a strategyproof (SP) mechanism is a game form in which each player has a weakly-dominant strategy, so that no player can gain by "spying" over the other players to know what they are going to play. When the players have private information (e.g. their type or their value to some item), and the strategy space of each player consists of the possible information values (e.g. possible types or values), a truthful mechanism is a game in which revealing the true information is a weakly-dominant strategy for each player. An SP mechanism is also called dominant-strategy-incentive-compatible (DSIC), to distinguish it from other kinds of incentive compatibility. A SP mechanism is immune to manipulations by individual players (but not by coalitions). In contrast, in a group strategyproof mechanism, no group of people can collude to misreport their preferences in a way that makes every member better off. In a strong group strategyproof mechanism, no group of people can col ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Social Choice
Social choice theory is a branch of welfare economics that extends the theory of rational choice to collective decision-making. Social choice studies the behavior of different mathematical procedures ( social welfare functions) used to combine individual preferences into a coherent whole.Amartya Sen (2008). "Social Choice". ''The New Palgrave Dictionary of Economics'', 2nd EditionAbstract & TOC./ref> It contrasts with political science in that it is a normative field that studies how a society can make good decisions, whereas political science is a descriptive field that observes how societies actually do make decisions. While social choice began as a branch of economics and decision theory, it has since received substantial contributions from mathematics, philosophy, political science, and game theory. Real-world examples of social choice rules include constitutions and parliamentary procedures for voting on laws, as well as electoral systems; as such, the field is occasionall ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Single-parameter Utility
In mechanism design, an agent is said to have single-parameter utility if his valuation of the possible outcomes can be represented by a single number. For example, in an auction for a single item, the utilities of all agents are single-parametric, since they can be represented by their monetary evaluation of the item. In contrast, in a combinatorial auction for two or more related items, the utilities are usually not single-parametric, since they are usually represented by their evaluations to all possible bundles of items. Notation There is a set X of possible outcomes. There are n agents which have different valuations for each outcome. In general, each agent can assign a different and unrelated value to every outcome in X. In the special case of single-parameter utility, each agent i has a publicly known outcome proper subset W_i \subset X which are the "winning outcomes" for agent i (e.g., in a single-item auction, W_i contains the outcome in which agent i wins the item). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Single Peaked Preferences
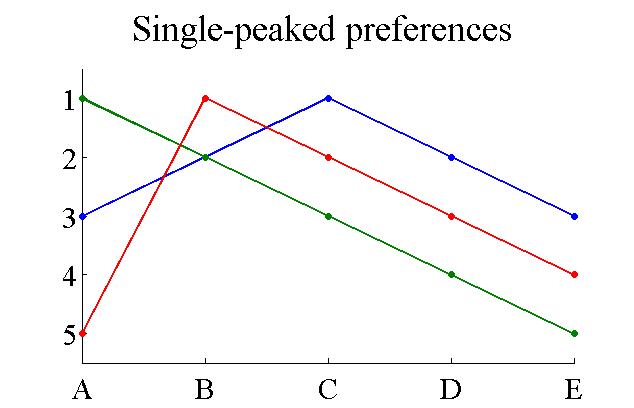
Single-peaked preferences are a class of preference relations. A group has single-peaked preferences over a set of outcomes if the outcomes can be ordered along a line such that: # Each agent has a "best outcome" in the set, and # For each agent, outcomes that are further from his or her best outcome are preferred less. Single-peaked preferences are typical of one-dimensional domains. A typical example is when several consumers have to decide on the amount of Public good (economics), public good to purchase. The amount is a one-dimensional variable. Usually, each consumer decides on a certain quantity which is best for him or her, and if the actual quantity is more/less than that ideal quantity, the agent is then less satisfied. With single-peaked preferences, there is a simple truthful mechanism for selecting an outcome, which is to select the median quantity; this results in the median voter theorem. It is truthful because the median function satisfies the Monotonicity (mechani ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Truthful Mechanism
In mechanism design, a strategyproof (SP) mechanism is a game form in which each player has a weakly- dominant strategy, so that no player can gain by "spying" over the other players to know what they are going to play. When the players have private information (e.g. their type or their value to some item), and the strategy space of each player consists of the possible information values (e.g. possible types or values), a truthful mechanism is a game in which revealing the true information is a weakly-dominant strategy for each player. An SP mechanism is also called dominant-strategy-incentive-compatible (DSIC), to distinguish it from other kinds of incentive compatibility. A SP mechanism is immune to manipulations by individual players (but not by coalitions). In contrast, in a group strategyproof mechanism, no group of people can collude to misreport their preferences in a way that makes every member better off. In a strong group strategyproof mechanism, no group of people can c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Median Voting Rule
The median voting rule or median mechanism is a rule for group decision-making along a one-dimensional domain. Each person votes by writing down his/her ideal value, and the rule selects a single value which is (in the basic mechanism) the ''median'' of all votes. Motivation Many scenarions of group decision making involve a one-dimensional domain. Some examples are: * Members of a city-council have to decide on the total amount of annual city budget. * Several people working in the same office have to decide on the air-conditioning temperature. * Parents of schoolchildren should decide how long the annual school vacation should be. * The public has to decide where to locate a facility along a one-dimensional street. Each member has in mind an ideal decision, called his "peak". Each agent prefers the actual amount to be as close as possible to his peak. A simple way to decide is the ''average voting rule'': ask each member what is his peak, and take the average of all peak ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cardinal Utility
In economics, a cardinal utility expresses not only which of two outcomes is preferred, but also the intensity of preferences, i.e. ''how much'' better or worse one outcome is compared to another. In consumer choice theory, economists originally attempted to replace cardinal utility with the apparently weaker concept of ordinal utility. Cardinal utility appears to impose the assumption that levels of absolute satisfaction exist, so magnitudes of increments to satisfaction can be compared across different situations. However, economists in the 1940s proved that under mild conditions, ordinal utilities imply cardinal utilities. This result is now known as the von Neumann–Morgenstern utility theorem; many similar utility representation theorems exist in other contexts. History In 1738, Daniel Bernoulli was the first to theorize about the marginal value of money. He assumed that the value of an additional amount is inversely proportional to the pecuniary possessions which a per ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Utilitarian
In ethical philosophy, utilitarianism is a family of normative ethical theories that prescribe actions that maximize happiness and well-being for the affected individuals. In other words, utilitarian ideas encourage actions that lead to the greatest good for the greatest number. Although different varieties of utilitarianism admit different characterizations, the basic idea that underpins them all is, in some sense, to maximize utility, which is often defined in terms of well-being or related concepts. For instance, Jeremy Bentham, the founder of utilitarianism, described ''utility'' as the capacity of actions or objects to produce benefits, such as pleasure, happiness, and good, or to prevent harm, such as pain and unhappiness, to those affected. Utilitarianism is a version of consequentialism, which states that the consequences of any action are the only standard of right and wrong. Unlike other forms of consequentialism, such as egoism and altruism, egalitarian utilita ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Makespan
In operations research Operations research () (U.S. Air Force Specialty Code: Operations Analysis), often shortened to the initialism OR, is a branch of applied mathematics that deals with the development and application of analytical methods to improve management and ..., the makespan of a project is the length of time that elapses from the start of work to the end. This type of multi-mode resource constrained project scheduling problem (MRCPSP) seeks to create the shortest logical project schedule, by efficiently using project resources, adding the lowest number of additional resources as possible to achieve the minimum makespan. The term commonly appears in the context of scheduling. Example There is a complex project that is composed of several sub-tasks. We would like to assign tasks to workers, such that the project finishes in the shortest possible time. As an example, suppose the "project" is to feed the goats. There are three goats to feed, one child can only feed on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |