|
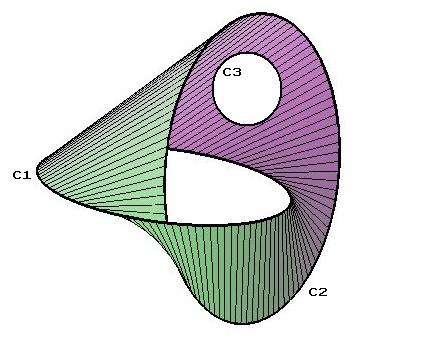
Möbius Energy
In mathematics, the Möbius energy of a knot (mathematics), knot is a particular knot energy, i.e., a Functional (mathematics), functional on the space of knots. It was discovered by Jun O'Hara, who demonstrated that the energy blows up as the knot's strands get close to one another. This is a useful property because it prevents self-intersection and ensures the result under gradient descent is of the same knot type. Invariance of Möbius energy under Möbius transformation#Higher dimensions, Möbius transformations was demonstrated by Michael Freedman, Zheng-Xu He, and Zhenghan Wang (1994) who used it to show the existence of a C^ energy minimizer in each isotopy class of a prime knot. They also showed the minimum energy of any knot conformation is achieved by a round circle. Conjecturally, there is no energy minimizer for composite knots. Robert B. Kusner and John M. Sullivan (mathematician), John M. Sullivan have done computer experiments with a discretized version of the Mö ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Link (knot Theory)
In mathematical knot theory, a link is a collection of knots which do not intersect, but which may be linked (or knotted) together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory. Implicit in this definition is that there is a ''trivial'' reference link, usually called the unlink, but the word is also sometimes used in context where there is no notion of a trivial link. For example, a co-dimension 2 link in 3-dimensional space is a subspace of 3-dimensional Euclidean space (or often the 3-sphere) whose connected components are homeomorphic to circles. The simplest nontrivial example of a link with more than one component is called the Hopf link, which consists of two circles (or unknots) linked together once. The circles in the Borromean rings are collectively linked despite the fact that no two of them are directly linked. The Borromean rings thus form a Brunnian link and in fact constit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ian Agol
Ian Agol (born May 13, 1970) is an American mathematician who deals primarily with the topology of three-dimensional manifolds. Education and career Agol graduated with B.S. in mathematics from the California Institute of Technology in 1992 and obtained his Ph.D. in 1998 from the University of California, San Diego. At UCSD, his advisor was Michael Freedman and his thesis was ''Topology of Hyperbolic 3-Manifolds''. He is a professor at the University of California, Berkeley and a former professor at the University of Illinois at Chicago. Contributions In 2004, Agol proved the Marden tameness conjecture, a conjecture of Albert Marden. It states that a hyperbolic 3-manifold with finitely generated fundamental group is homeomorphic to the interior of a compact 3-manifold. The conjecture was also independently proven by Danny Calegari and David Gabai, and implies the Ahlfors measure conjecture. In 2012 he announced a proof of the virtually Haken conjecture, which was publishe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hopf Link
In mathematical knot theory, the Hopf link is the simplest nontrivial link with more than one component. It consists of two circles linked together exactly once, and is named after Heinz Hopf. Geometric realization A concrete model consists of two unit circles in perpendicular planes, each passing through the center of the other.. See in particulap. 77 This model minimizes the ropelength of the link and until 2002 the Hopf link was the only link whose ropelength was known. The convex hull of these two circles forms a shape called an oloid. Properties Depending on the relative orientations of the two components the linking number of the Hopf link is ±1. The Hopf link is a (2,2)-torus link with the braid word :\sigma_1^2.\, The knot complement of the Hopf link is R × ''S''1 × ''S''1, the cylinder over a torus. This space has a locally Euclidean geometry, so the Hopf link is not a hyperbolic link. The knot group of the Hopf link (the fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
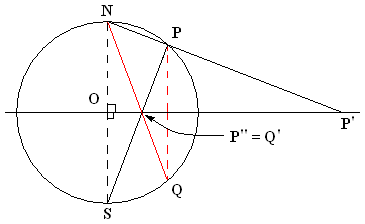
Stereographic Projection
In mathematics, a stereographic projection is a perspective projection of the sphere, through a specific point on the sphere (the ''pole'' or ''center of projection''), onto a plane (the ''projection plane'') perpendicular to the diameter through the point. It is a smooth, bijective function from the entire sphere except the center of projection to the entire plane. It maps circles on the sphere to circles or lines on the plane, and is conformal, meaning that it preserves angles at which curves meet and thus locally approximately preserves shapes. It is neither isometric (distance preserving) nor equiareal (area preserving). The stereographic projection gives a way to represent a sphere by a plane. The metric induced by the inverse stereographic projection from the plane to the sphere defines a geodesic distance between points in the plane equal to the spherical distance between the spherical points they represent. A two-dimensional coordinate system on the stereo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Link (knot Theory)
In mathematical knot theory, a link is a collection of knots which do not intersect, but which may be linked (or knotted) together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory. Implicit in this definition is that there is a ''trivial'' reference link, usually called the unlink, but the word is also sometimes used in context where there is no notion of a trivial link. For example, a co-dimension 2 link in 3-dimensional space is a subspace of 3-dimensional Euclidean space (or often the 3-sphere) whose connected components are homeomorphic to circles. The simplest nontrivial example of a link with more than one component is called the Hopf link, which consists of two circles (or unknots) linked together once. The circles in the Borromean rings are collectively linked despite the fact that no two of them are directly linked. The Borromean rings thus form a Brunnian link and in fact constit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alexander Polynomial
In mathematics, the Alexander polynomial is a knot invariant which assigns a polynomial with integer coefficients to each knot type. James Waddell Alexander II discovered this, the first knot polynomial, in 1923. In 1969, John Conway showed a version of this polynomial, now called the Alexander–Conway polynomial, could be computed using a skein relation, although its significance was not realized until the discovery of the Jones polynomial in 1984. Soon after Conway's reworking of the Alexander polynomial, it was realized that a similar skein relation was exhibited in Alexander's paper on his polynomial. Definition Let ''K'' be a knot in the 3-sphere. Let ''X'' be the infinite cyclic cover of the knot complement of ''K''. This covering can be obtained by cutting the knot complement along a Seifert surface of ''K'' and gluing together infinitely many copies of the resulting manifold with boundary in a cyclic manner. There is a covering transformation ''t'' acting on ''X'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unknotting Problem
In mathematics, the unknotting problem is the problem of algorithmically recognizing the unknot, given some representation of a knot, e.g., a knot diagram. There are several types of unknotting algorithms. A major unresolved challenge is to determine if the problem admits a polynomial time algorithm; that is, whether the problem lies in the complexity class P. Computational complexity First steps toward determining the computational complexity were undertaken in proving that the problem is in larger complexity classes, which contain the class P. By using normal surfaces to describe the Seifert surfaces of a given knot, showed that the unknotting problem is in the complexity class NP. claimed the weaker result that unknotting is in AM ∩ co-AM; however, later they retracted this claim. In 2011, Greg Kuperberg proved that (assuming the generalized Riemann hypothesis) the unknotting problem is in co-NP, and in 2016, Marc Lackenby provided an unconditional pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unknot
In the mathematical theory of knots, the unknot, not knot, or trivial knot, is the least knotted of all knots. Intuitively, the unknot is a closed loop of rope without a knot tied into it, unknotted. To a knot theorist, an unknot is any embedded topological circle in the 3-sphere that is ambient isotopic (that is, deformable) to a geometrically round circle, the standard unknot. The unknot is the only knot that is the boundary of an embedded disk, which gives the characterization that only unknots have Seifert genus 0. Similarly, the unknot is the identity element with respect to the knot sum operation. Unknotting problem Deciding if a particular knot is the unknot was a major driving force behind knot invariants, since it was thought this approach would possibly give an efficient algorithm to recognize the unknot from some presentation such as a knot diagram. Unknot recognition is known to be in both NP and co-NP. It is known that knot Floer homology and K ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wolfgang Haken
Wolfgang Haken (June 21, 1928 – October 2, 2022) was a German American mathematician who specialized in topology, in particular 3-manifolds. Biography Haken was born in Berlin, Germany. His father was Werner Haken, a physicist who had Max Planck as a doctoral thesis advisor. In 1953, Haken earned a Ph.D. degree in mathematics from Christian-Albrechts-Universität zu Kiel (Kiel University) and married Anna-Irmgard von Bredow, who earned a Ph.D. degree in mathematics from the same university in 1959. In 1962, they left Germany so he could accept a position as visiting professor at the University of Illinois at Urbana-Champaign. He became a full professor in 1965, retiring in 1998. In 1976, together with colleague Kenneth Appel at the University of Illinois at Urbana-Champaign, Haken solved the four-color theorem. They proved that any two-dimensional map, with certain limitations, can be filled in with four colors without any adjacent “countries” sharing the same color ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algorithm
In mathematics and computer science, an algorithm () is a finite sequence of rigorous instructions, typically used to solve a class of specific problems or to perform a computation. Algorithms are used as specifications for performing calculations and data processing. More advanced algorithms can perform automated deductions (referred to as automated reasoning) and use mathematical and logical tests to divert the code execution through various routes (referred to as automated decision-making). Using human characteristics as descriptors of machines in metaphorical ways was already practiced by Alan Turing with terms such as "memory", "search" and "stimulus". In contrast, a heuristic is an approach to problem solving that may not be fully specified or may not guarantee correct or optimal results, especially in problem domains where there is no well-defined correct or optimal result. As an effective method, an algorithm can be expressed within a finite amount of space ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ambient Isotopy
In the mathematical subject of topology, an ambient isotopy, also called an ''h-isotopy'', is a kind of continuous distortion of an ambient space, for example a manifold, taking a submanifold to another submanifold. For example in knot theory, one considers two knots the same if one can distort one knot into the other without breaking it. Such a distortion is an example of an ambient isotopy. More precisely, let N and M be manifolds and g and h be embeddings of N in M. A continuous map :F:M \times ,1\rightarrow M is defined to be an ambient isotopy taking g to h if F_0 is the identity map, each map F_t is a homeomorphism from M to itself, and F_1 \circ g = h. This implies that the orientation must be preserved by ambient isotopies. For example, two knots that are mirror images of each other are, in general, not equivalent. See also * Isotopy * Regular homotopy *Regular isotopy References *M. A. Armstrong, ''Basic Topology'', Springer-Verlag Springer Science+Bus ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |