|
Multiscale Turbulence
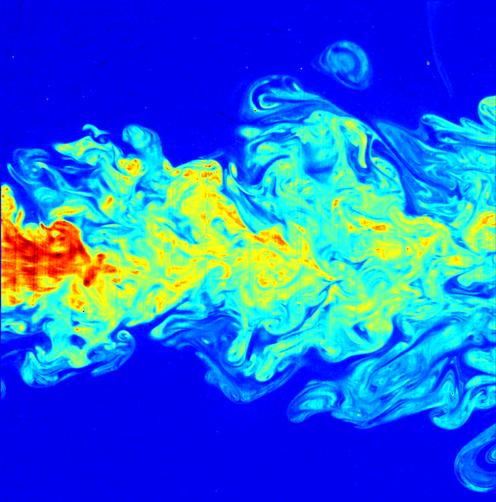
Multiscale turbulence is a class of Turbulence, turbulent flows in which the chaotic motion of the fluid is forced at different length and/or time scales. This is usually achieved by immersing in a moving fluid a body with a multiscale, often fractal-like, arrangement of length scales. This arrangement of scales can be either passive or Automatic control, active As Turbulence, turbulent flows contain Eddy (fluid dynamics), eddies with a wide range of scales, exciting the turbulence at particular scales (or range of scales) allows one to fine-tune the properties of that flow. Multiscale turbulent flows have been successfully applied in different fields., such as: * Reducing acoustic noise from wings by modifying the geometry of Spoiler (aeronautics), spoilers; * Enhancing heat transfer from impinging jets passing through grids; * Reducing the vortex shedding intensity of flows past normal plates without changing the Vortex shedding, shedding frequency; * Enhancing mixing by energ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Turbulence
In fluid dynamics, turbulence or turbulent flow is fluid motion characterized by chaotic changes in pressure and flow velocity. It is in contrast to a laminar flow, which occurs when a fluid flows in parallel layers, with no disruption between those layers. Turbulence is commonly observed in everyday phenomena such as surf, fast flowing rivers, billowing storm clouds, or smoke from a chimney, and most fluid flows occurring in nature or created in engineering applications are turbulent. Turbulence is caused by excessive kinetic energy in parts of a fluid flow, which overcomes the damping effect of the fluid's viscosity. For this reason turbulence is commonly realized in low viscosity fluids. In general terms, in turbulent flow, unsteady vortices appear of many sizes which interact with each other, consequently drag due to friction effects increases. This increases the energy needed to pump fluid through a pipe. The onset of turbulence can be predicted by the dimensionless Rey ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dissipation
In thermodynamics, dissipation is the result of an irreversible process that takes place in homogeneous thermodynamic systems. In a dissipative process, energy (internal, bulk flow kinetic, or system potential) transforms from an initial form to a final form, where the capacity of the final form to do thermodynamic work is less than that of the initial form. For example, heat transfer is dissipative because it is a transfer of internal energy from a hotter body to a colder one. Following the second law of thermodynamics, the entropy varies with temperature (reduces the capacity of the combination of the two bodies to do work), but never decreases in an isolated system. These processes produce entropy at a certain rate. The entropy production rate times ambient temperature gives the dissipated power. Important examples of irreversible processes are: heat flow through a thermal resistance, fluid flow through a flow resistance, diffusion (mixing), chemical reactions, and electric cu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kolmogorov Microscales
In fluid dynamics, Kolmogorov microscales are the smallest scales in the turbulent flow of fluids. At the Kolmogorov scale, viscosity dominates and the turbulence kinetic energy is dissipated into thermal energy. They are defined by where * is the average rate of dissipation of turbulence kinetic energy per unit mass, and * is the kinematic viscosity of the fluid. Typical values of the Kolmogorov length scale, for atmospheric motion in which the large eddies have length scales on the order of kilometers, range from 0.1 to 10 millimeters; for smaller flows such as in laboratory systems, may be much smaller. In 1941, Andrey Kolmogorov introduced the hypothesis that the smallest scales of turbulence are universal (similar for every turbulent flow) and that they depend only on and . The definitions of the Kolmogorov microscales can be obtained using this idea and dimensional analysis. Since the dimension of kinematic viscosity is length2/time, and the dimension of the energy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dissipation
In thermodynamics, dissipation is the result of an irreversible process that affects a thermodynamic system. In a dissipative process, energy ( internal, bulk flow kinetic, or system potential) transforms from an initial form to a final form, where the capacity of the final form to do thermodynamic work is less than that of the initial form. For example, transfer of energy as heat is dissipative because it is a transfer of energy other than by thermodynamic work or by transfer of matter, and spreads previously concentrated energy. Following the second law of thermodynamics, in conduction and radiation from one body to another, the entropy varies with temperature (reduces the capacity of the combination of the two bodies to do work), but never decreases in an isolated system. In mechanical engineering, dissipation is the irreversible conversion of mechanical energy into thermal energy with an associated increase in entropy. Processes with defined local temperature ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
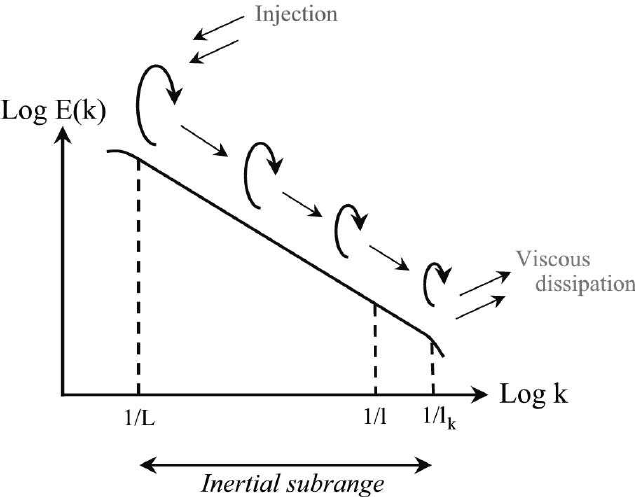
Energy Cascade
In continuum mechanics, an energy cascade involves the transfer of energy from large scales of motion to the small scales (called a direct energy cascade) or a transfer of energy from the small scales to the large scales (called an inverse energy cascade). This transfer of energy between different scales requires that the dynamics of the system is nonlinear. Strictly speaking, a cascade requires the energy transfer to be local in scale (only between fluctuations of nearly the same size), evoking a cascading waterfall from pool to pool without long-range transfers across the scale domain. This concept plays an important role in the study of well-developed turbulence. It was memorably expressed in this poem by Lewis F. Richardson in the 1920s. Energy cascades are also important for wind waves in the theory of wave turbulence. Consider for instance turbulence generated by the air flow around a tall building: the energy-containing eddies generated by flow separation have sizes of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Turbulence Kinetic Energy
In fluid dynamics, turbulence kinetic energy (TKE) is the mean kinetic energy per unit mass associated with eddies in turbulent flow. Physically, the turbulence kinetic energy is characterised by measured root-mean-square (RMS) velocity fluctuations. In the Reynolds-averaged Navier Stokes equations, the turbulence kinetic energy can be calculated based on the closure method, i.e. a turbulence model. Generally, the TKE is defined to be half the sum of the variances (square of standard deviations) of the velocity components: k = \frac12 \left(\, \overline + \overline + \overline \,\right), where the turbulent velocity component is the difference between the instantaneous and the average velocity u' = u - \overline, whose mean and variance are \overline = \frac \int_0^T (u(t) - \overline) \, dt = 0 and \overline = \frac\int_0^T (u(t) - \overline)^2 \, dt \geq 0 , respectively. TKE can be produced by fluid shear, friction or buoyancy, or through external forcing at low-frequency ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Root Mean Square
In mathematics and its applications, the root mean square of a set of numbers x_i (abbreviated as RMS, or rms and denoted in formulas as either x_\mathrm or \mathrm_x) is defined as the square root of the mean square (the arithmetic mean of the squares) of the set. The RMS is also known as the quadratic mean (denoted M_2) and is a particular case of the generalized mean. The RMS of a continuously varying function (denoted f_\mathrm) can be defined in terms of an integral of the squares of the instantaneous values during a cycle. For alternating electric current, RMS is equal to the value of the constant direct current that would produce the same power dissipation in a resistive load. In estimation theory, the root-mean-square deviation of an estimator is a measure of the imperfection of the fit of the estimator to the data. Definition The RMS value of a set of values (or a continuous-time waveform) is the square root of the arithmetic mean of the squares of the values, or th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Length Scale
In physics, length scale is a particular length or distance determined with the precision of at most a few orders of magnitude. The concept of length scale is particularly important because physical phenomena of different length scales cannot affect each other and are said to decouple. The decoupling of different length scales makes it possible to have a self-consistent theory that only describes the relevant length scales for a given problem. Scientific reductionism says that the physical laws on the shortest length scales can be used to derive the effective description at larger length scales. The idea that one can derive descriptions of physics at different length scales from one another can be quantified with the renormalization group. In quantum mechanics the length scale of a given phenomenon is related to its de Broglie wavelength \ell = \hbar/p where \hbar is the reduced Planck's constant and p is the momentum that is being probed. In relativistic mechanics time an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Freestream
The freestream is the air far upstream of an aerodynamic Aerodynamics, from grc, ἀήρ ''aero'' (air) + grc, δυναμική (dynamics), is the study of the motion of air, particularly when affected by a solid object, such as an airplane wing. It involves topics covered in the field of fluid dyn ... body, that is, before the body has a chance to deflect, slow down or compress the air. Freestream conditions are usually denoted with a \infty symbol, e.g. V_\infty, meaning the freestream velocity. References *Anderson, John D., 1989. ''Introduction to Flight'', 3rd Ed. McGraw-Hill Aerodynamics {{Fluiddynamics-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reynolds Number
In fluid mechanics, the Reynolds number () is a dimensionless quantity that helps predict fluid flow patterns in different situations by measuring the ratio between inertial and viscous forces. At low Reynolds numbers, flows tend to be dominated by laminar (sheet-like) flow, while at high Reynolds numbers flows tend to be turbulent. The turbulence results from differences in the fluid's speed and direction, which may sometimes intersect or even move counter to the overall direction of the flow ( eddy currents). These eddy currents begin to churn the flow, using up energy in the process, which for liquids increases the chances of cavitation. The Reynolds number has wide applications, ranging from liquid flow in a pipe to the passage of air over an aircraft wing. It is used to predict the transition from laminar to turbulent flow and is used in the scaling of similar but different-sized flow situations, such as between an aircraft model in a wind tunnel and the full-size ve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Energy Cascade
In continuum mechanics, an energy cascade involves the transfer of energy from large scales of motion to the small scales (called a direct energy cascade) or a transfer of energy from the small scales to the large scales (called an inverse energy cascade). This transfer of energy between different scales requires that the dynamics of the system is nonlinear. Strictly speaking, a cascade requires the energy transfer to be local in scale (only between fluctuations of nearly the same size), evoking a cascading waterfall from pool to pool without long-range transfers across the scale domain. This concept plays an important role in the study of well-developed turbulence. It was memorably expressed in this poem by Lewis F. Richardson in the 1920s. Energy cascades are also important for wind waves in the theory of wave turbulence. Consider for instance turbulence generated by the air flow around a tall building: the energy-containing eddies generated by flow separation have sizes of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Andrey Kolmogorov
Andrey Nikolaevich Kolmogorov ( rus, Андре́й Никола́евич Колмого́ров, p=ɐnˈdrʲej nʲɪkɐˈlajɪvʲɪtɕ kəlmɐˈɡorəf, a=Ru-Andrey Nikolaevich Kolmogorov.ogg, 25 April 1903 – 20 October 1987) was a Soviet mathematician who contributed to the mathematics of probability theory, topology, intuitionistic logic, turbulence, classical mechanics, algorithmic information theory and computational complexity. Biography Early life Andrey Kolmogorov was born in Tambov, about 500 kilometers south-southeast of Moscow, in 1903. His unmarried mother, Maria Y. Kolmogorova, died giving birth to him. Andrey was raised by two of his aunts in Tunoshna (near Yaroslavl) at the estate of his grandfather, a well-to-do nobleman. Little is known about Andrey's father. He was supposedly named Nikolai Matveevich Kataev and had been an agronomist. Kataev had been exiled from St. Petersburg to the Yaroslavl province after his participation in the revolutionary movem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |