|
Multi-compartment Model
A multi-compartment model is a type of mathematical model used for describing the way materials or energies are transmitted among the ''compartments'' of a system. Sometimes, the physical system that we try to model in equations is too complex, so it is much easier to discretize the problem and reduce the number of parameters. Each compartment is assumed to be a homogeneous entity within which the entities being modeled are equivalent. A multi-compartment model is classified as a lumped parameters model. Similar to more general mathematical models, multi-compartment models can treat variables as continuous, such as a differential equation, or as discrete, such as a Markov chain. Depending on the system being modeled, they can be treated as stochastic or deterministic. Multi-compartment models are used in many fields including pharmacokinetics, epidemiology, biomedicine, systems theory, complexity theory, engineering, physics, information science and social science. The circuits sy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used in the natural sciences (such as physics, biology, earth science, chemistry) and engineering disciplines (such as computer science, electrical engineering), as well as in non-physical systems such as the social sciences (such as economics, psychology, sociology, political science). The use of mathematical models to solve problems in business or military operations is a large part of the field of operations research. Mathematical models are also used in music, linguistics, and philosophy (for example, intensively in analytic philosophy). A model may help to explain a system and to study the effects of different components, and to make predictions about behavior. Elements of a mathematical model Mathematical models can take many forms, including dynamical systems, statis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
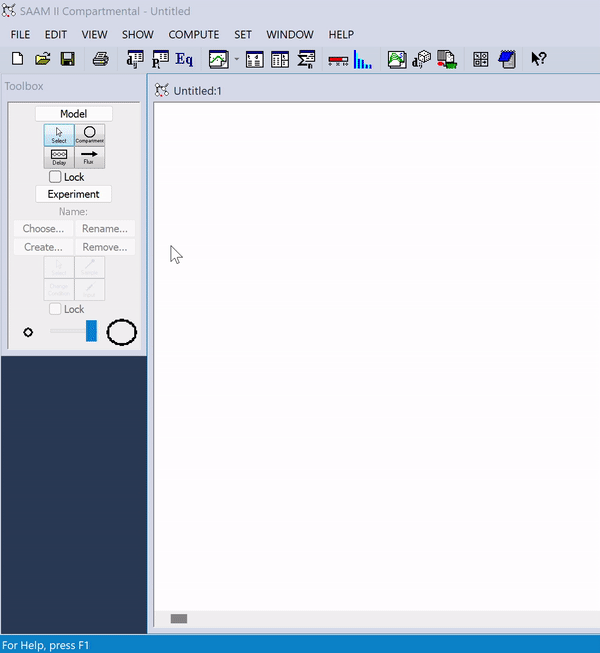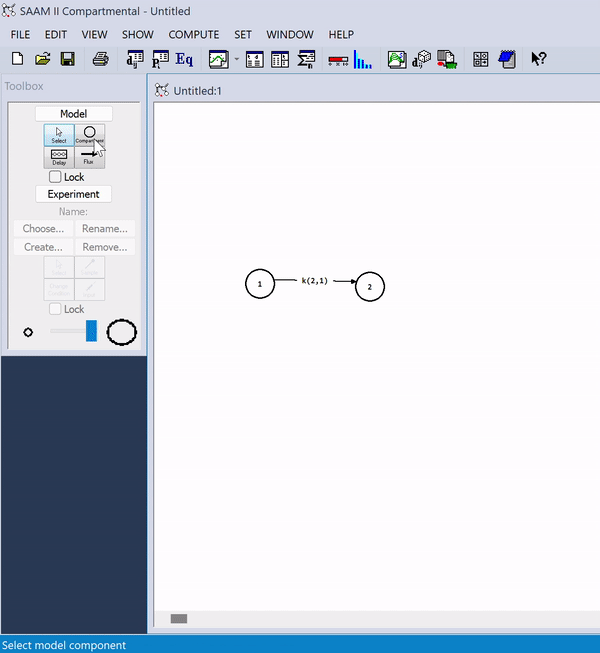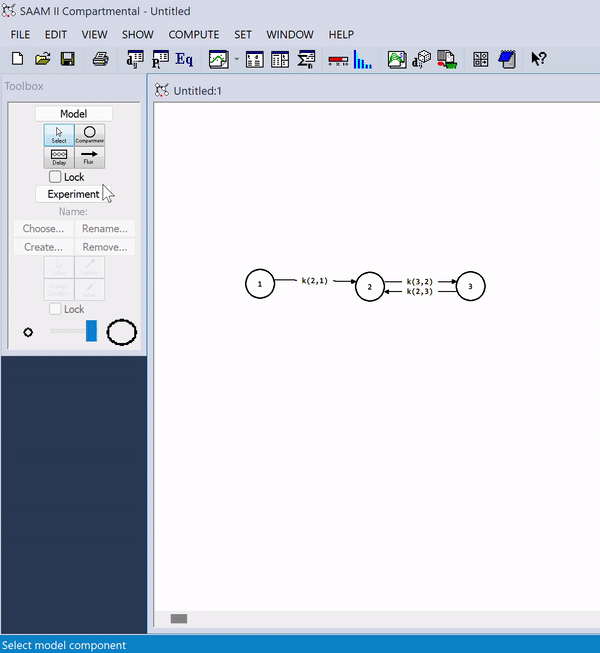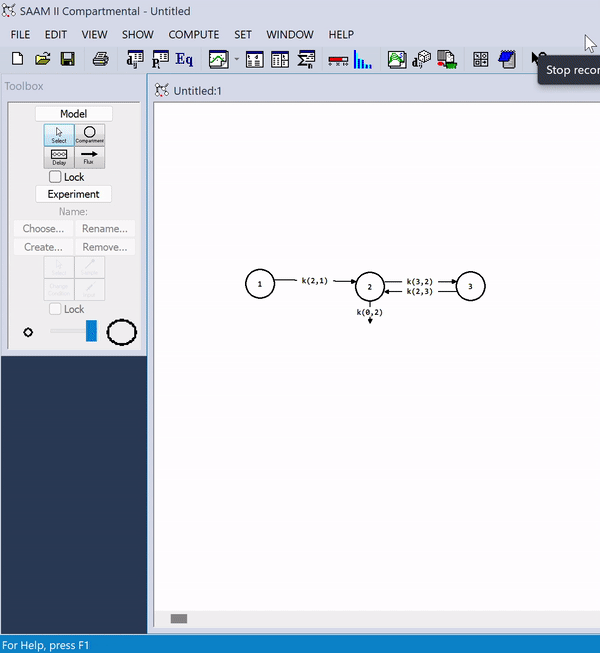
SAAM II
SAAM II, short for "Simulation Analysis and Modeling" version 2.0, is a renowned computer program designed for scientific research in the field of bioscience. It is a descriptive and exploratory tool in drug development, tracers, metabolic disorders, and pharmacokinetics/pharmacodynamics research. It is grounded in the principles of multi-compartment model theory, which is a widely-used approach for modeling complex biological systems. SAAM II facilitates the construction and simulation of models, providing researchers with a friendly user interface allowing the quick run and multi-fitting of simple and complex (linear and nonlinear) structures and data. SAAM II is used by many Pharma and Pharmacy Schools as a drug development, research, and educational tool. Features The compartmental module SAAM II offers a user-friendly interface that eliminates the need for coding. Within the compartmental module, users can construct models effortlessly by drag-and-dropping various model com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physiologically-based Pharmacokinetic Modelling
Physiologically based pharmacokinetic (PBPK) modeling is a mathematical modeling technique for predicting the absorption, distribution, metabolism and excretion (ADME) of synthetic or natural chemical substances in humans and other animal species. PBPK modeling is used in pharmaceutical research and drug development, and in health risk assessment for cosmetics or general chemicals. PBPK models strive to be mechanistic by mathematically transcribing anatomical, physiological, physical, and chemical descriptions of the phenomena involved in the complex ADME processes. A large degree of residual simplification and empiricism is still present in those models, but they have an extended domain of applicability compared to that of classical, empirical function based, pharmacokinetic models. PBPK models may have purely predictive uses, but other uses, such as statistical inference, have been made possible by the development of Bayesian statistical tools able to deal with complex models. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compartmental Models In Epidemiology
Compartmental models are a very general modelling technique. They are often applied to the mathematical modelling of infectious diseases. The population is assigned to compartments with labels – for example, S, I, or R, (Susceptible, Infectious, or Recovered). People may progress between compartments. The order of the labels usually shows the flow patterns between the compartments; for example SEIS means susceptible, exposed, infectious, then susceptible again. The origin of such models is the early 20th century, with important works being that of Ross in 1916, Ross and Hudson in 1917, Kermack and McKendrick in 1927 and Kendall in 1956. The Reed-Frost model was also a significant and widely-overlooked ancestor of modern epidemiological modelling approaches. The models are most often run with ordinary differential equations (which are deterministic), but can also be used with a stochastic (random) framework, which is more realistic but much more complicated to analyze. Mod ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Biological Neuron Models
Biological neuron models, also known as a spiking neuron models, are mathematical descriptions of the properties of certain cells in the nervous system that generate sharp electrical potentials across their cell membrane, roughly one millisecond in duration, called action potentials or spikes (Fig. 2). Since spikes are transmitted along the axon and synapses from the sending neuron to many other neurons, spiking neurons are considered to be a major information processing unit of the nervous system. Spiking neuron models can be divided into different categories: the most detailed mathematical models are biophysical neuron models (also called Hodgkin-Huxley models) that describe the membrane voltage as a function of the input current and the activation of ion channels. Mathematically simpler are integrate-and-fire models that describe the membrane voltage as a function of the input current and predict the spike times without a description of the biophysical processes that shape ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Biomedical Engineering
Biomedical engineering (BME) or medical engineering is the application of engineering principles and design concepts to medicine and biology for healthcare purposes (e.g., diagnostic or therapeutic). BME is also traditionally logical sciences to advance health care treatment, including diagnosis, monitoring, and therapy. Also included under the scope of a biomedical engineer is the management of current medical equipment in hospitals while adhering to relevant industry standards. This involves procurement, routine testing, preventive maintenance, and making equipment recommendations, a role also known as a Biomedical Equipment Technician (BMET) or as clinical engineering. Biomedical engineering has recently emerged as its own study, as compared to many other engineering fields. Such an evolution is common as a new field transition from being an interdisciplinary specialization among already-established fields to being considered a field in itself. Much of the work in biomedi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used in the natural sciences (such as physics, biology, earth science, chemistry) and engineering disciplines (such as computer science, electrical engineering), as well as in non-physical systems such as the social sciences (such as economics, psychology, sociology, political science). The use of mathematical models to solve problems in business or military operations is a large part of the field of operations research. Mathematical models are also used in music, linguistics, and philosophy (for example, intensively in analytic philosophy). A model may help to explain a system and to study the effects of different components, and to make predictions about behavior. Elements of a mathematical model Mathematical models can take many forms, including dynamical systems, statis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenvalues And Eigenvectors
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted by \lambda, is the factor by which the eigenvector is scaled. Geometrically, an eigenvector, corresponding to a real nonzero eigenvalue, points in a direction in which it is stretched by the transformation and the eigenvalue is the factor by which it is stretched. If the eigenvalue is negative, the direction is reversed. Loosely speaking, in a multidimensional vector space, the eigenvector is not rotated. Formal definition If is a linear transformation from a vector space over a field into itself and is a nonzero vector in , then is an eigenvector of if is a scalar multiple of . This can be written as T(\mathbf) = \lambda \mathbf, where is a scalar in , known as the eigenvalue, characteristic value, or characteristic root ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Law Of Mass Action
In chemistry, the law of mass action is the proposition that the rate of the chemical reaction is directly proportional to the product of the activities or concentrations of the reactants. It explains and predicts behaviors of solutions in dynamic equilibrium. Specifically, it implies that for a chemical reaction mixture that is in equilibrium, the ratio between the concentration of reactants and products is constant. Two aspects are involved in the initial formulation of the law: 1) the equilibrium aspect, concerning the composition of a reaction mixture at equilibrium and 2) the kinetic aspect concerning the rate equations for elementary reactions. Both aspects stem from the research performed by Cato M. Guldberg and Peter Waage between 1864 and 1879 in which equilibrium constants were derived by using kinetic data and the rate equation which they had proposed. Guldberg and Waage also recognized that chemical equilibrium is a dynamic process in which rates of reaction ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lotka–Volterra Equations
The Lotka–Volterra equations, also known as the predator–prey equations, are a pair of first-order nonlinear differential equations, frequently used to describe the dynamics of biological systems in which two species interact, one as a predator and the other as prey. The populations change through time according to the pair of equations: \begin \frac &= \alpha x - \beta x y, \\ \frac &= \delta x y - \gamma y, \end where * is the number of prey (for example, rabbits); * is the number of some predator (for example, foxes); *\tfrac and \tfrac represent the instantaneous growth rates of the two populations; * represents time; *, , , are positive real parameters describing the interaction of the two species. The Lotka–Volterra system of equations is an example of a Kolmogorov model, which is a more general framework that can model the dynamics of ecological systems with predator–prey interactions, competition, disease, and mutualism. History The Lotka–Volterra predat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
MATLAB
MATLAB (an abbreviation of "MATrix LABoratory") is a proprietary multi-paradigm programming language and numeric computing environment developed by MathWorks. MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages. Although MATLAB is intended primarily for numeric computing, an optional toolbox uses the MuPAD symbolic engine allowing access to symbolic computing abilities. An additional package, Simulink, adds graphical multi-domain simulation and model-based design for dynamic and embedded systems. As of 2020, MATLAB has more than 4 million users worldwide. They come from various backgrounds of engineering, science, and economics. History Origins MATLAB was invented by mathematician and computer programmer Cleve Moler. The idea for MATLAB was based on his 1960s PhD thesis. Moler became a math professor at the University of New Mexico an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solute
In chemistry, a solution is a special type of homogeneous mixture composed of two or more substances. In such a mixture, a solute is a substance dissolved in another substance, known as a solvent. If the attractive forces between the solvent and solute particles are greater than the attractive forces holding the solute particles together, the solvent particles pull the solute particles apart and surround them. These surrounded solute particles then move away from the solid solute and out into the solution. The mixing process of a solution happens at a scale where the effects of chemical polarity are involved, resulting in interactions that are specific to solvation. The solution usually has the state of the solvent when the solvent is the larger fraction of the mixture, as is commonly the case. One important parameter of a solution is the concentration, which is a measure of the amount of solute in a given amount of solution or solvent. The term " aqueous solution" is use ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |