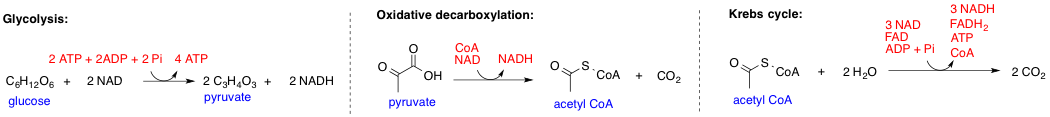|
Metabolic Control Theory
Metabolic control analysis (MCA) is a mathematical framework for describing metabolic, signaling, and genetic pathways. MCA quantifies how variables,elastsuch as fluxes and species concentrations, depend on network parameters. In particular, it is able to describe how network-dependent properties, called control coefficients, depend on local properties called elasticities or Elasticity Coefficients. MCA was originally developed to describe the control in metabolic pathways but was subsequently extended to describe signaling and genetic networks. MCA has sometimes also been referred to as ''Metabolic Control Theory,'' but this terminology was rather strongly opposed by Henrik Kacser, one of the founders. More recent work has shown that MCA can be mapped directly on to classical control theory and are as such equivalent. Biochemical systems theory is a similar formalism, though with rather different objectives. Both are evolutions of an earlier theoretical analysis by Joseph Higgi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Metabolic Pathway
In biochemistry, a metabolic pathway is a linked series of chemical reactions occurring within a cell. The reactants, products, and intermediates of an enzymatic reaction are known as metabolites, which are modified by a sequence of chemical reactions catalyzed by enzymes. In most cases of a metabolic pathway, the product of one enzyme acts as the substrate for the next. However, side products are considered waste and removed from the cell. These enzymes often require dietary minerals, vitamins, and other cofactors to function. Different metabolic pathways function based on the position within a eukaryotic cell and the significance of the pathway in the given compartment of the cell. For instance, the, electron transport chain, and oxidative phosphorylation all take place in the mitochondrial membrane. In contrast, glycolysis, pentose phosphate pathway, and fatty acid biosynthesis all occur in the cytosol of a cell. There are two types of metabolic pathways that are character ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Steady State
In systems theory, a system or a Process theory, process is in a steady state if the variables (called state variables) which define the behavior of the system or the process are unchanging in time. In continuous time, this means that for those properties ''p'' of the system, the partial derivative with respect to time is zero and remains so: : \frac = 0 \quad \text t. In discrete time, it means that the first difference of each property is zero and remains so: :p_t-p_=0 \quad \text t. The concept of a steady state has relevance in many fields, in particular thermodynamics, Steady state economy, economics, and engineering. If a system is in a steady state, then the recently observed behavior of the system will continue into the future. In stochastic systems, the probabilities that various states will be repeated will remain constant. See for example Linear difference equation#Conversion to homogeneous form for the derivation of the steady state. In many systems, a steady state i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boundary (thermodynamic)
A thermodynamic system is a body of matter and/or radiation, confined in space by walls, with defined permeabilities, which separate it from its surroundings. The surroundings may include other thermodynamic systems, or physical systems that are not thermodynamic systems. A wall of a thermodynamic system may be purely notional, when it is described as being 'permeable' to all matter, all radiation, and all forces. A state of a thermodynamic system can be fully described in several different ways, by several different sets of thermodynamic state variables. A widely used distinction is between ''isolated'', ''closed'', and ''open'' thermodynamic systems. An isolated thermodynamic system has walls that are non-conductive of heat and perfectly reflective of all radiation, that are rigid and immovable, and that are impermeable to all forms of matter and all forces. (Some writers use the word 'closed' when here the word 'isolated' is being used.) A closed thermodynamic system is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trivial (mathematics)
In mathematics, the adjective trivial is often used to refer to a claim or a case which can be readily obtained from context, or an object which possesses a simple structure (e.g., groups, topological spaces). The noun triviality usually refers to a simple technical aspect of some proof or definition. The origin of the term in mathematical language comes from the medieval trivium curriculum, which distinguishes from the more difficult quadrivium curriculum. The opposite of trivial is nontrivial, which is commonly used to indicate that an example or a solution is not simple, or that a statement or a theorem is not easy to prove. The judgement of whether a situation under consideration is trivial or not depends on who considers it since the situation is obviously true for someone who has sufficient knowledge or experience of it while to someone who has never seen this, it may be even hard to be understood so not trivial at all. And there can be an argument about how quickly and easily ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Closed-form Expression
In mathematics, a closed-form expression is a mathematical expression that uses a finite number of standard operations. It may contain constants, variables, certain well-known operations (e.g., + − × ÷), and functions (e.g., ''n''th root, exponent, logarithm, trigonometric functions, and inverse hyperbolic functions), but usually no limit, differentiation, or integration. The set of operations and functions may vary with author and context. Example: roots of polynomials The solutions of any quadratic equation with complex coefficients can be expressed in closed form in terms of addition, subtraction, multiplication, division, and square root extraction, each of which is an elementary function. For example, the quadratic equation :ax^2+bx+c=0, is tractable since its solutions can be expressed as a closed-form expression, i.e. in terms of elementary functions: :x=\frac. Similarly, solutions of cubic and quartic (third and fourth degree) equations can be expresse ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chemical Kinetics
Chemical kinetics, also known as reaction kinetics, is the branch of physical chemistry that is concerned with understanding the rates of chemical reactions. It is to be contrasted with chemical thermodynamics, which deals with the direction in which a reaction occurs but in itself tells nothing about its rate. Chemical kinetics includes investigations of how experimental conditions influence the speed of a chemical reaction and yield information about the reaction's mechanism and transition states, as well as the construction of mathematical models that also can describe the characteristics of a chemical reaction. History In 1864, Peter Waage and Cato Guldberg pioneered the development of chemical kinetics by formulating the law of mass action, which states that the speed of a chemical reaction is proportional to the quantity of the reacting substances.C.M. Guldberg and P. Waage,"Studies Concerning Affinity" ''Forhandlinger i Videnskabs-Selskabet i Christiania'' (1864), 35P. W ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Connectivity (graph Theory)
In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements (nodes or edges) that need to be removed to separate the remaining nodes into two or more isolated subgraphs. It is closely related to the theory of network flow problems. The connectivity of a graph is an important measure of its resilience as a network. Connected vertices and graphs In an undirected graph , two '' vertices'' and are called connected if contains a path from to . Otherwise, they are called disconnected. If the two vertices are additionally connected by a path of length , i.e. by a single edge, the vertices are called adjacent. A graph is said to be connected if every pair of vertices in the graph is connected. This means that there is a path between every pair of vertices. An undirected graph that is not connected is called disconnected. An undirected graph ''G'' is therefore disconnected if there exist two vertices ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elasticity Coefficient
The rate of a chemical reaction is influenced by many different factors, such as temperature, pH, reactant, and product concentrations and other effectors. The degree to which these factors change the reaction rate is described by the elasticity coefficient. This coefficient is defined as follows: : \varepsilon_^v=\left(\frac \frac\right)_=\frac \approx \frac where v denotes the reaction rate and s denotes the substrate concentration. Be aware that the notation will use lowercase roman letters, such as s, to indicate concentrations. The partial derivative in the definition indicates that the elasticity is measured with respect to changes in a factor S while keeping all other factors constant. The most common factors include substrates, products, and effectors. The scaling of the coefficient ensures that it is dimensionless and independent of the units used to measure the reaction rate and magnitude of the factor. The elasticity coefficient is an integral part of metabolic con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chemical Reaction
A chemical reaction is a process that leads to the IUPAC nomenclature for organic transformations, chemical transformation of one set of chemical substances to another. Classically, chemical reactions encompass changes that only involve the positions of electrons in the forming and breaking of chemical bonds between atoms, with no change to the Atomic nucleus, nuclei (no change to the elements present), and can often be described by a chemical equation. Nuclear chemistry is a sub-discipline of chemistry that involves the chemical reactions of unstable and radioactive Chemical element, elements where both electronic and nuclear changes can occur. The substance (or substances) initially involved in a chemical reaction are called reagent, reactants or reagents. Chemical reactions are usually characterized by a chemical change, and they yield one or more Product (chemistry), products, which usually have properties different from the reactants. Reactions often consist of a sequence o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logical Implication
Logical consequence (also entailment) is a fundamental concept in logic, which describes the relationship between statements that hold true when one statement logically ''follows from'' one or more statements. A valid logical argument is one in which the conclusion is entailed by the premises, because the conclusion is the consequence of the premises. The philosophical analysis of logical consequence involves the questions: In what sense does a conclusion follow from its premises? and What does it mean for a conclusion to be a consequence of premises?Beall, JC and Restall, Greg, Logical Consequence' The Stanford Encyclopedia of Philosophy (Fall 2009 Edition), Edward N. Zalta (ed.). All of philosophical logic is meant to provide accounts of the nature of logical consequence and the nature of logical truth. Logical consequence is necessary and formal, by way of examples that explain with formal proof and models of interpretation. A sentence is said to be a logical consequ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Summation
In mathematics, summation is the addition of a sequence of any kind of numbers, called ''addends'' or ''summands''; the result is their ''sum'' or ''total''. Beside numbers, other types of values can be summed as well: functions, vectors, matrices, polynomials and, in general, elements of any type of mathematical objects on which an operation denoted "+" is defined. Summations of infinite sequences are called series. They involve the concept of limit, and are not considered in this article. The summation of an explicit sequence is denoted as a succession of additions. For example, summation of is denoted , and results in 9, that is, . Because addition is associative and commutative, there is no need of parentheses, and the result is the same irrespective of the order of the summands. Summation of a sequence of only one element results in this element itself. Summation of an empty sequence (a sequence with no elements), by convention, results in 0. Very often, the elements ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |