|
Melnikov Distance
In mathematics, the Melnikov method is a tool to identify the existence of chaos in a class of dynamical systems under periodic perturbation. Introduction The Melnikov method is used in many cases to predict the occurrence of chaotic orbits in non-autonomous smooth nonlinear systems under periodic perturbation. According to the method, it is possible to construct a function called the "Melnikov function" which can be used to predict either regular or chaotic behavior of a dynamical system. Thus, the Melnikov function will be used to determine a measure of distance between stable and unstable manifolds in the Poincaré map. Moreover, when this measure is equal to zero, by the method, those manifolds crossed each other transversally and from that crossing the system will become chaotic. This method appeared in 1890 by H. Poincaré and by V. Melnikov in 1963 and could be called the "Poincaré-Melnikov Method". Moreover, it was described by several textbooks as Guckenheimer & Holme ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chaos Theory
Chaos theory is an interdisciplinary area of scientific study and branch of mathematics focused on underlying patterns and deterministic laws of dynamical systems that are highly sensitive to initial conditions, and were once thought to have completely random states of disorder and irregularities. Chaos theory states that within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnection, constant feedback loops, repetition, self-similarity, fractals, and self-organization. The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state (meaning that there is sensitive dependence on initial conditions). A metaphor for this behavior is that a butterfly flapping its wings in Brazil can cause a tornado in Texas. Small differences in initial conditions, such as those due to errors in measurements or due to rounding errors i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamical System
In mathematics, a dynamical system is a system in which a Function (mathematics), function describes the time dependence of a Point (geometry), point in an ambient space. Examples include the mathematical models that describe the swinging of a clock pendulum, fluid dynamics, the flow of water in a pipe, the Brownian motion, random motion of particles in the air, and population dynamics, the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real number, real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a Set (mathematics), set, without the need of a Differentiability, smooth space-time structure defined on it. At any given time, a dynamical system has a State ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
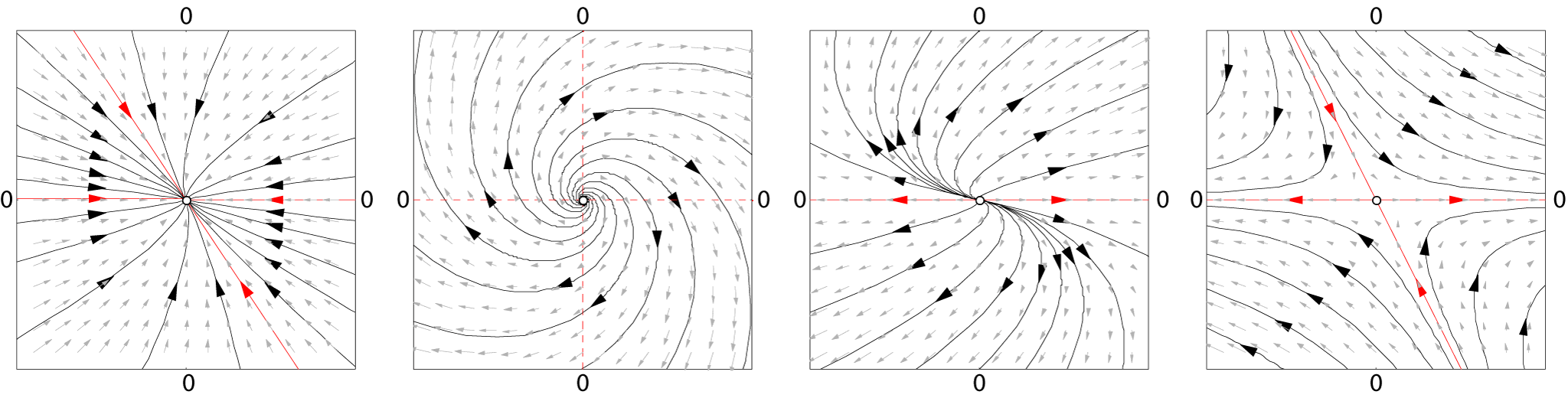
Stable Manifold
In mathematics, and in particular the study of dynamical systems, the idea of ''stable and unstable sets'' or stable and unstable manifolds give a formal mathematical definition to the general notions embodied in the idea of an attractor or repellor. In the case of hyperbolic dynamics, the corresponding notion is that of the hyperbolic set. Physical example The gravitational tidal forces acting on the rings of Saturn provide an easy-to-visualize physical example. The tidal forces flatten the ring into the equatorial plane, even as they stretch it out in the radial direction. Imagining the rings to be sand or gravel particles ("dust") in orbit around Saturn, the tidal forces are such that any perturbations that push particles above or below the equatorial plane results in that particle feeling a restoring force, pushing it back into the plane. Particles effectively oscillate in a harmonic well, damped by collisions. The stable direction is perpendicular to the ring. The unstable di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kolmogorov–Arnold–Moser Theorem
The Kolmogorov–Arnold–Moser (KAM) theorem is a result in dynamical systems about the persistence of quasiperiodic motions under small perturbations. The theorem partly resolves the small-divisor problem that arises in the perturbation theory of classical mechanics. The problem is whether or not a small perturbation of a conservative dynamical system results in a lasting quasiperiodic orbit. The original breakthrough to this problem was given by Andrey Kolmogorov in 1954. This was rigorously proved and extended by Jürgen Moser in 1962 (for smooth twist maps) and Vladimir Arnold in 1963 (for analytic Hamiltonian systems), and the general result is known as the KAM theorem. Arnold originally thought that this theorem could apply to the motions of the Solar System or other instances of the -body problem, but it turned out to work only for the three-body problem because of a degeneracy in his formulation of the problem for larger numbers of bodies. Later, Gabriella Pinzari showe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamiltonian System
A Hamiltonian system is a dynamical system governed by Hamilton's equations. In physics, this dynamical system describes the evolution of a physical system such as a planetary system or an electron in an electromagnetic field. These systems can be studied in both Hamiltonian mechanics and dynamical systems theory. Overview Informally, a Hamiltonian system is a mathematical formalism developed by Hamilton to describe the evolution equations of a physical system. The advantage of this description is that it gives important insights into the dynamics, even if the initial value problem cannot be solved analytically. One example is the planetary movement of three bodies: while there is no closed-form solution to the general problem, Poincaré showed for the first time that it exhibits deterministic chaos. Formally, a Hamiltonian system is a dynamical system characterised by the scalar function H(\boldsymbol,\boldsymbol,t), also known as the Hamiltonian. The state of the system, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homoclinic Bifurcation
Bifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family of curves, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations. Most commonly applied to the mathematical study of dynamical systems, a bifurcation occurs when a small smooth change made to the parameter values (the bifurcation parameters) of a system causes a sudden 'qualitative' or topological change in its behavior. Bifurcations occur in both continuous systems (described by ordinary, delay or partial differential equations) and discrete systems (described by maps). The name "bifurcation" was first introduced by Henri Poincaré in 1885 in the first paper in mathematics showing such a behavior. Henri Poincaré also later named various types of stationary points and classified them . Bifurcation types It is useful to divide bifurcations into two principal classes: * Local bifurcations, which can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase Space
In dynamical system theory, a phase space is a space in which all possible states of a system are represented, with each possible state corresponding to one unique point in the phase space. For mechanical systems, the phase space usually consists of all possible values of position and momentum variables. It is the outer product of direct space and reciprocal space. The concept of phase space was developed in the late 19th century by Ludwig Boltzmann, Henri Poincaré, and Josiah Willard Gibbs. Introduction In a phase space, every degree of freedom or parameter of the system is represented as an axis of a multidimensional space; a one-dimensional system is called a phase line, while a two-dimensional system is called a phase plane. For every possible state of the system or allowed combination of values of the system's parameters, a point is included in the multidimensional space. The system's evolving state over time traces a path (a phase-space trajectory for the system) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Periodi Orbit
Clementine literature (also called Clementina, Pseudo-Clementine Writings, Kerygmata Petrou, Clementine Romance) is the name given to the religious romance which purports to contain a record made by one Clement (whom the narrative identifies as both Pope Clement I, and Domitian's cousin Titus Flavius Clemens) of discourses involving the Apostle Peter, together with an account of the circumstances under which Clement came to be Peter's travelling companion, and of other details of Clement's family history. The author is sometimes called Pseudo-Clement (as distinct from Pope Clement I). Overview Two versions of this romance have survived: one version is called the ''Clementine Homilies'' (''H''), which consists of 20 books and exists in the original Greek; the other is called the ''Clementine Recognitions'' (''R''), for which the original Greek has been lost, but exists in a Latin translation made by Tyrannius Rufinus (died 410). Two later epitomes of the ''Homilies'' also exis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Vector
In geometry, a normal is an object such as a line, ray, or vector that is perpendicular to a given object. For example, the normal line to a plane curve at a given point is the (infinite) line perpendicular to the tangent line to the curve at the point. A normal vector may have length one (a unit vector) or its length may represent the curvature of the object (a ''curvature vector''); its algebraic sign may indicate sides (interior or exterior). In three dimensions, a surface normal, or simply normal, to a surface at point P is a vector perpendicular to the tangent plane of the surface at P. The word "normal" is also used as an adjective: a line ''normal'' to a plane, the ''normal'' component of a force, the normal vector, etc. The concept of normality generalizes to orthogonality (right angles). The concept has been generalized to differentiable manifolds of arbitrary dimension embedded in a Euclidean space. The normal vector space or normal space of a manifold at point P ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homoclinic Connection
{{unreferenced, date=December 2010 In dynamical systems, a branch of mathematics, a structure formed from the stable manifold and unstable manifold of a fixed point. Definition for maps Let f:M\to M be a map defined on a manifold M, with a fixed point p. Let W^s(f,p) and W^u(f,p) be the stable manifold and the unstable manifold of the fixed point p, respectively. Let V be a connected invariant manifold such that : V\subseteq W^s(f,p)\cap W^u(f,p) Then V is called a homoclinic connection. Heteroclinic connection It is a similar notion, but it refers to two fixed points, p and q. The condition satisfied by V is replaced with: :V\subseteq W^s(f,p)\cap W^u(f,q) This notion is not symmetric with respect to p and q. Homoclinic and heteroclinic intersections When the invariant manifolds W^s(f,p) and W^u(f,q), possibly with p=q, intersect but there is no homoclinic/heteroclinic connection, a different structure is formed by the two manifolds, sometimes referred to as the homoclini ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Splitting
Splitting may refer to: * Splitting (psychology) * Lumpers and splitters, in classification or taxonomy * Wood splitting * Tongue splitting * Splitting, railway operation Mathematics * Heegaard splitting * Splitting field * Splitting principle * Splitting theorem * Splitting lemma * for the numerical method to solve differential equations, see Symplectic integrator See also * Split (other) Split(s) or The Split may refer to: Places * Split, Croatia, the largest coastal city in Croatia * Split Island, Canada, an island in the Hudson Bay * Split Island, Falkland Islands * Split Island, Fiji, better known as Hạfliua Arts, enterta ... * Splitter (other) {{disambig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crossing Of The Homoclinic Manifolds In The Normal Vector
Crossing may refer to: * ''Crossing'' (2008 film), a South Korean film * ''Crossing'' (album), a 1985 album by world music/jazz group Oregon * Crossing (architecture), the junction of the four arms of a cruciform church * Crossing (knot theory), a visualization of intersections in mathematical knots * Crossing (physics), the relation between particle and antiparticle scattering * Crossing (plant), deliberate interbreeding of plants * Crossing oneself, a ritual hand motion made by some Christians * William Crossing (1847–1928), English writer * Intersection (road), also known as a crossing * Level crossing, a railway crossing a street See also * Crossings (other) * The Crossing (other) * Cross (other) A cross is a geometrical figure consisting of two intersecting lines or bars. Cross or The Cross may also refer to: Religion * Christian cross, the basic symbol of Christianity * Cross necklace, a necklace worn by adherents of the Christian r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |