|
Median Test
In statistics, Mood's median test is a special case of Pearson's chi-squared test. It is a nonparametric test that tests the null hypothesis that the medians of the populations from which two or more samples are drawn are identical. The data in each sample are assigned to two groups, one consisting of data whose values are higher than the median value in the two groups combined, and the other consisting of data whose values are at the median or below. A Pearson's chi-squared test is then used to determine whether the observed frequencies in each sample differ from expected frequencies derived from a distribution combining the two groups. Relation to other tests The test has low power (efficiency) for moderate to large sample sizes. The Wilcoxon– Mann–Whitney U two-sample test or its generalisation for more samples, the Kruskal–Wallis test, can often be considered instead. The relevant aspect of the median test is that it only considers the position of each observation relati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ''wikt:Statistik#German, Statistik'', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pearson's Chi-squared Test
Pearson's chi-squared test (\chi^2) is a statistical test applied to sets of categorical data to evaluate how likely it is that any observed difference between the sets arose by chance. It is the most widely used of many chi-squared tests (e.g., Yates, likelihood ratio, portmanteau test in time series, etc.) – statistical procedures whose results are evaluated by reference to the chi-squared distribution. Its properties were first investigated by Karl Pearson in 1900. In contexts where it is important to improve a distinction between the test statistic and its distribution, names similar to ''Pearson χ-squared'' test or statistic are used. It tests a null hypothesis stating that the frequency distribution of certain events observed in a sample is consistent with a particular theoretical distribution. The events considered must be mutually exclusive and have total probability 1. A common case for this is where the events each cover an outcome of a categorical variable. A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonparametric Test
Nonparametric statistics is the branch of statistics that is not based solely on parametrized families of probability distributions (common examples of parameters are the mean and variance). Nonparametric statistics is based on either being distribution-free or having a specified distribution but with the distribution's parameters unspecified. Nonparametric statistics includes both descriptive statistics and statistical inference. Nonparametric tests are often used when the assumptions of parametric tests are violated. Definitions The term "nonparametric statistics" has been imprecisely defined in the following two ways, among others: Applications and purpose Non-parametric methods are widely used for studying populations that take on a ranked order (such as movie reviews receiving one to four stars). The use of non-parametric methods may be necessary when data have a ranking but no clear numerical interpretation, such as when assessing preferences. In terms of levels of me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Null Hypothesis
In scientific research, the null hypothesis (often denoted ''H''0) is the claim that no difference or relationship exists between two sets of data or variables being analyzed. The null hypothesis is that any experimentally observed difference is due to chance alone, and an underlying causative relationship does not exist, hence the term "null". In addition to the null hypothesis, an alternative hypothesis is also developed, which claims that a relationship does exist between two variables. Basic definitions The ''null hypothesis'' and the ''alternative hypothesis'' are types of conjectures used in statistical tests, which are formal methods of reaching conclusions or making decisions on the basis of data. The hypotheses are conjectures about a statistical model of the population, which are based on a sample of the population. The tests are core elements of statistical inference, heavily used in the interpretation of scientific experimental data, to separate scientific claims fr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Median
In statistics and probability theory, the median is the value separating the higher half from the lower half of a data sample, a population, or a probability distribution. For a data set, it may be thought of as "the middle" value. The basic feature of the median in describing data compared to the mean (often simply described as the "average") is that it is not skewed by a small proportion of extremely large or small values, and therefore provides a better representation of a "typical" value. Median income, for example, may be a better way to suggest what a "typical" income is, because income distribution can be very skewed. The median is of central importance in robust statistics, as it is the most resistant statistic, having a breakdown point of 50%: so long as no more than half the data are contaminated, the median is not an arbitrarily large or small result. Finite data set of numbers The median of a finite list of numbers is the "middle" number, when those numbers are list ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Population
In statistics, a population is a set of similar items or events which is of interest for some question or experiment. A statistical population can be a group of existing objects (e.g. the set of all stars within the Milky Way galaxy) or a hypothetical and potentially infinite group of objects conceived as a generalization from experience (e.g. the set of all possible hands in a game of poker). A common aim of statistical analysis is to produce information about some chosen population. In statistical inference, a subset of the population (a statistical ''sample'') is chosen to represent the population in a statistical analysis. Moreover, the statistical sample must be unbiased and accurately model the population (every unit of the population has an equal chance of selection). The ratio of the size of this statistical sample to the size of the population is called a ''sampling fraction''. It is then possible to estimate the ''population parameters'' using the appropriate sample s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sampling (statistics)
In statistics, quality assurance, and survey methodology, sampling is the selection of a subset (a statistical sample) of individuals from within a statistical population to estimate characteristics of the whole population. Statisticians attempt to collect samples that are representative of the population in question. Sampling has lower costs and faster data collection than measuring the entire population and can provide insights in cases where it is infeasible to measure an entire population. Each observation measures one or more properties (such as weight, location, colour or mass) of independent objects or individuals. In survey sampling, weights can be applied to the data to adjust for the sample design, particularly in stratified sampling. Results from probability theory and statistical theory are employed to guide the practice. In business and medical research, sampling is widely used for gathering information about a population. Acceptance sampling is used to determine if ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frequency Distribution
In statistics, the frequency (or absolute frequency) of an event i is the number n_i of times the observation has occurred/recorded in an experiment or study. These frequencies are often depicted graphically or in tabular form. Types The cumulative frequency is the total of the absolute frequencies of all events at or below a certain point in an ordered list of events. The (or empirical probability) of an event is the absolute frequency normalized by the total number of events: : f_i = \frac = \frac. The values of f_i for all events i can be plotted to produce a frequency distribution. In the case when n_i = 0 for certain i, pseudocounts can be added. Depicting frequency distributions A frequency distribution shows us a summarized grouping of data divided into mutually exclusive classes and the number of occurrences in a class. It is a way of showing unorganized data notably to show results of an election, income of people for a certain region, sales of a product within ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
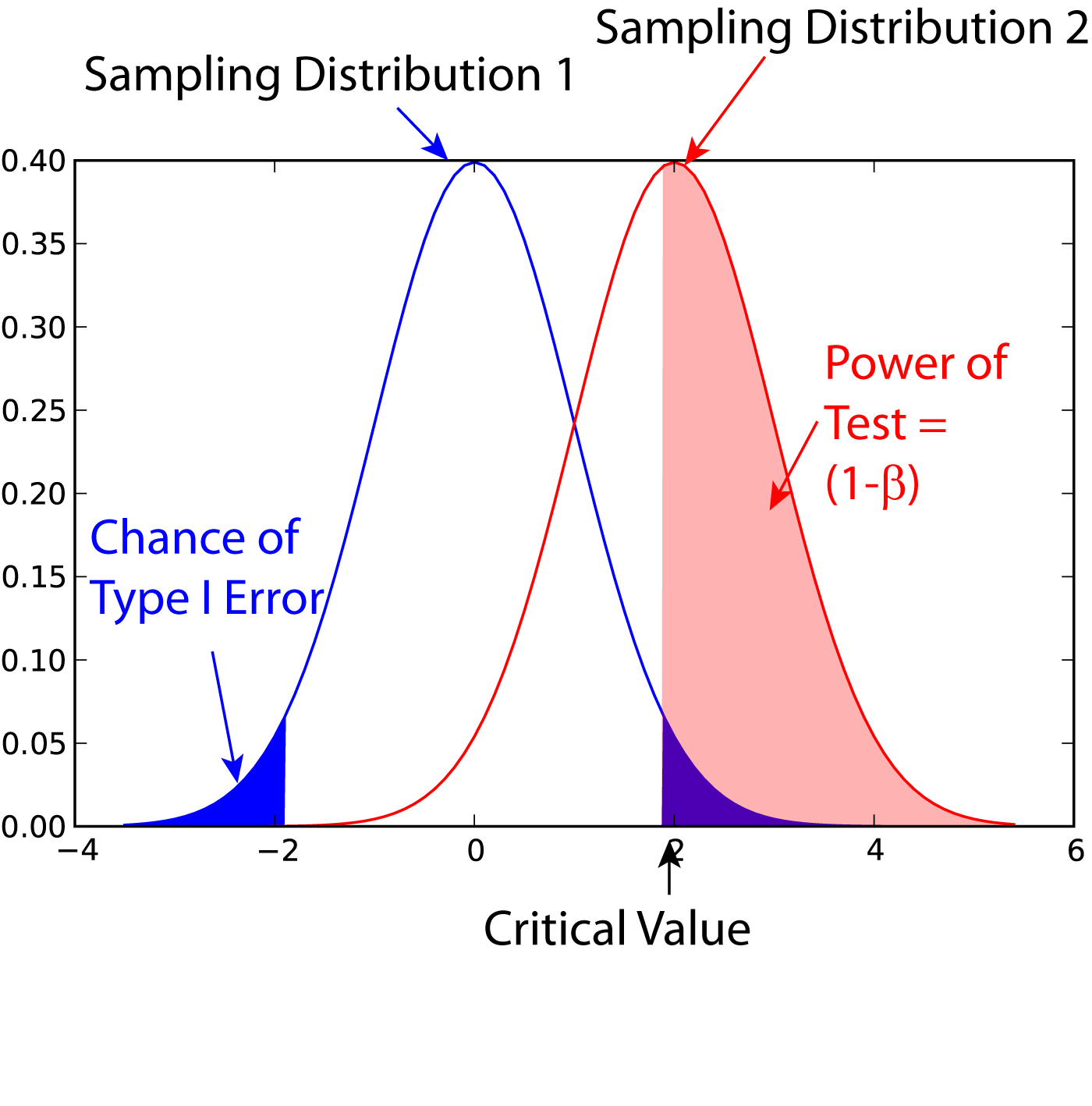
Statistical Power
In statistics, the power of a binary hypothesis test is the probability that the test correctly rejects the null hypothesis (H_0) when a specific alternative hypothesis (H_1) is true. It is commonly denoted by 1-\beta, and represents the chances of a true positive detection conditional on the actual existence of an effect to detect. Statistical power ranges from 0 to 1, and as the power of a test increases, the probability \beta of making a type II error by wrongly failing to reject the null hypothesis decreases. Notation This article uses the following notation: * ''β'' = probability of a Type II error, known as a "false negative" * 1 − ''β'' = probability of a "true positive", i.e., correctly rejecting the null hypothesis. "1 − ''β''" is also known as the power of the test. * ''α'' = probability of a Type I error, known as a "false positive" * 1 − ''α'' = probability of a "true negative", i.e., correctly not rejecting the null hypothesis Description For a ty ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kruskal–Wallis One-way Analysis Of Variance
The Kruskal–Wallis test by ranks, Kruskal–Wallis ''H'' testKruskal–Wallis H Test using SPSS Statistics Laerd Statistics (named after and ), or one-way ANOVA on ranks is a method for testing whether samples originate from the same distribution. It is used for comparing two or more independent sample ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sign Test
The sign test is a statistical method to test for consistent differences between pairs of observations, such as the weight of subjects before and after treatment. Given pairs of observations (such as weight pre- and post-treatment) for each subject, the sign test determines if one member of the pair (such as pre-treatment) tends to be greater than (or less than) the other member of the pair (such as post-treatment). The paired observations may be designated ''x'' and ''y''. For comparisons of paired observations (''x'',y), the sign test is most useful if comparisons can only be expressed as ''x'' > ''y'', ''x'' = ''y'', or ''x'' 0. Assuming that H0 is true, then ''W'' follows a binomial distribution ''W'' ~ b(''m'', 0.5). Assumptions Let ''Z''i = ''Y''i – ''X''i for ''i'' = 1, ... , ''n''. # The differences ''Zi'' are assumed to be independent. # Each ''Zi'' comes from the same continuous population. # The values ''X''''i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |