|
McKelvey–Schofield Chaos Theorem
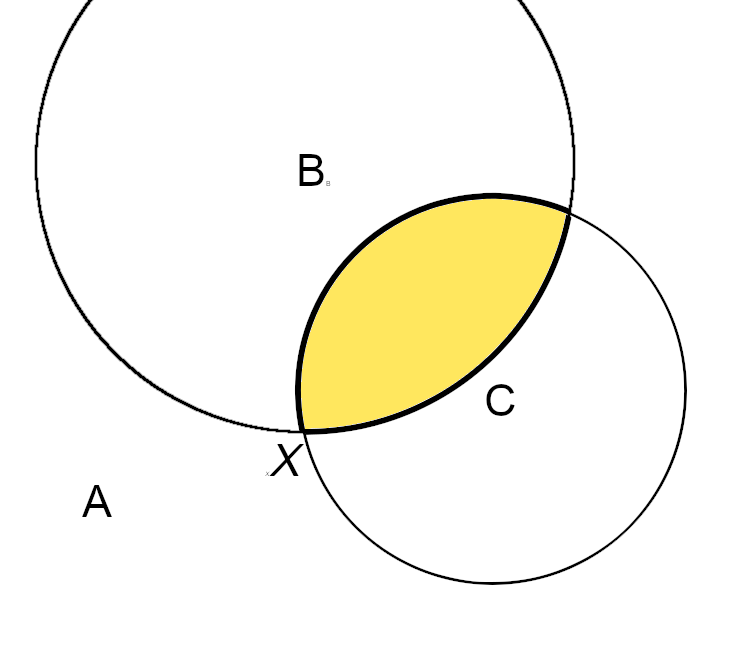
The McKelvey–Schofield chaos theorem is a result in social choice theory. It states that if preferences are defined over a multidimensional policy space, then majority rule is in general unstable: there is no Condorcet winner. Furthermore, any point in the space can be reached from any other point by a sequence of majority votes. The theorem can be thought of as showing that Arrow's impossibility theorem holds when preferences are restricted to be concave in \mathbb^. The median voter theorem shows that when preferences are restricted to be single-peaked on the real line, Arrow's theorem does not hold, and the median voter's ideal point is a Condorcet winner. The chaos theorem shows that this good news does not continue in multiple dimensions. Richard McKelvey initially proved the theorem for Euclidean preferences. Norman Schofield extended the theorem to the more general class of concave preferences. The figure shows an example. There are three voters in the electorate, wit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Social Choice Theory
Social choice theory or social choice is a theoretical framework for analysis of combining individual opinions, preferences, interests, or welfares to reach a ''collective decision'' or ''social welfare'' in some sense. Amartya Sen (2008). "Social Choice,". ''The New Palgrave Dictionary of Economics'', 2nd EditionAbstract & TOC./ref> Whereas choice theory is concerned with individuals making choices based on their preferences, social choice theory is concerned with how to translate the preferences of individuals into the preferences of a group. A non-theoretical example of a collective decision is enacting a law or set of laws under a constitution. Another example is voting, where individual preferences over candidates are collected to elect a person that best represents the group's preferences. Social choice blends elements of welfare economics and public choice theory. It is methodologically individualistic, in that it aggregates preferences and behaviors of individual mem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Condorcet Winner
An electoral system satisfies the Condorcet winner criterion () if it always chooses the Condorcet winner when one exists. The candidate who wins a majority of the vote in every head-to-head election against each of the other candidatesthat is, a candidate preferred by more voters than any othersis the Condorcet winner, although Condorcet winners do not exist in all cases. It is sometimes simply referred to as the "Condorcet criterion", though it is very different from the "Condorcet loser criterion". Any voting method conforming to the Condorcet winner criterion is known as a Condorcet method. The Condorcet winner is the person who would win a two-candidate election against each of the other candidates in a plurality vote. For a set of candidates, the Condorcet winner is always the same regardless of the voting system in question, and can be discovered by using pairwise counting on voters' ranked preferences. A Condorcet winner will not always exist in a given set of votes, which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arrow's Impossibility Theorem
Arrow's impossibility theorem, the general possibility theorem or Arrow's paradox is an impossibility theorem in social choice theory that states that when voters have three or more distinct alternatives (options), no ranked voting electoral system can convert the ranked preferences of individuals into a community-wide (complete and transitive) ranking while also meeting the specified set of criteria: ''unrestricted domain'', ''non-dictatorship'', '' Pareto efficiency'', and '' independence of irrelevant alternatives''. The theorem is often cited in discussions of voting theory as it is further interpreted by the Gibbard–Satterthwaite theorem. The theorem is named after economist and Nobel laureate Kenneth Arrow, who demonstrated the theorem in his doctoral thesis and popularized it in his 1951 book '' Social Choice and Individual Values''. The original paper was titled "A Difficulty in the Concept of Social Welfare". In short, the theorem states that no rank-order electoral ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Concave Function
In mathematics, a concave function is the negative of a convex function. A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap, or upper convex. Definition A real-valued function f on an interval (or, more generally, a convex set in vector space) is said to be ''concave'' if, for any x and y in the interval and for any \alpha \in ,1/math>, :f((1-\alpha )x+\alpha y)\geq (1-\alpha ) f(x)+\alpha f(y) A function is called ''strictly concave'' if :f((1-\alpha )x + \alpha y) > (1-\alpha) f(x) + \alpha f(y)\, for any \alpha \in (0,1) and x \neq y. For a function f: \mathbb \to \mathbb, this second definition merely states that for every z strictly between x and y, the point (z, f(z)) on the graph of f is above the straight line joining the points (x, f(x)) and (y, f(y)). A function f is quasiconcave if the upper contour sets of the function S(a)=\ are convex sets. Properties Functions of a single variable # A differentia ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Median Voter Theorem
The median voter theorem is a proposition relating to ranked preference voting put forward by Duncan Black in 1948.Duncan Black, "On the Rationale of Group Decision-making" (1948). It states that if voters and policies are distributed along a one-dimensional spectrum, with voters ranking alternatives in order of proximity, then any voting method which satisfies the Condorcet criterion will elect the candidate closest to the median voter. In particular, a majority vote between two options will do so. The theorem is associated with public choice economics and statistical political science. Partha Dasgupta and Eric Maskin have argued that it provides a powerful justification for voting methods based on the Condorcet criterion. Plott's majority rule equilibrium theorem extends this to two dimensions. A loosely related assertion had been made earlier (in 1929) by Harold Hotelling. It is not a true theorem and is more properly known as the median voter theory or median voter model. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Richard McKelvey
Richard Drummond McKelvey (April 27, 1944 – April 22, 2002) was a political scientist, specializing in mathematical theories of voting. He received his BS in Mathematics from Oberlin College, MA in mathematics from Washington University in St. Louis, and PhD in political science from University of Rochester. He was an Econometric Society fellow, and was the Edie and Lew Wasserman Professor of Political Science at the California Institute of Technology until his death, from cancer, in 2002. McKelvey also wrote several articles about instability. One discussed the topic agenda manipulation. The McKelvey theorem indicates that almost every possible outcome can be realized through democratic decision-making, by smartly choosing the order or agenda in which decisions are taken. The desired result is established by ensuring that in each stage another composition of the majority determines the outcome of that part of the decision-making procedure. The person who designs the decision ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Relation
In mathematics, Euclidean relations are a class of binary relations that formalize " Axiom 1" in Euclid's ''Elements'': "Magnitudes which are equal to the same are equal to each other." Definition A binary relation ''R'' on a set ''X'' is Euclidean (sometimes called right Euclidean) if it satisfies the following: for every ''a'', ''b'', ''c'' in ''X'', if ''a'' is related to ''b'' and ''c'', then ''b'' is related to ''c''.. To write this in predicate logic: :\forall a, b, c\in X\,(a\,R\, b \land a \,R\, c \to b \,R\, c). Dually, a relation ''R'' on ''X'' is left Euclidean if for every ''a'', ''b'', ''c'' in ''X'', if ''b'' is related to ''a'' and ''c'' is related to ''a'', then ''b'' is related to ''c'': :\forall a, b, c\in X\,(b\,R\, a \land c \,R\, a \to b \,R\, c). Properties # Due to the commutativity of ∧ in the definition's antecedent, ''aRb'' ∧ ''aRc'' even implies ''bRc'' ∧ ''cRb'' when ''R'' is right Euclidean. Similarly, ''bRa'' ∧ ''cRa'' implies ''bRc'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Norman Schofield
Norman James Schofield (January 30, 1944 – October 12, 2019) was a Scottish-American political scientist, the Dr. William Taussig Professor of Political Economy at the Washington University in St. Louis.Curriculum vitae retrieved 2012-03-03.. Early life and education Schofield earned two bachelor's degrees from the ; one in physics in 1965 and the other in mathematics in 1966. Later he obtained two PhDs from : the first in government in 1976 and the second in economics in 1985. ...[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Indifference Curves
In economics, an indifference curve connects points on a graph representing different quantities of two goods, points between which a consumer is ''indifferent''. That is, any combinations of two products indicated by the curve will provide the consumer with equal levels of utility, and the consumer has no preference for one combination or bundle of goods over a different combination on the same curve. One can also refer to each point on the indifference curve as rendering the same level of utility (satisfaction) for the consumer. In other words, an indifference curve is the locus of various points showing different combinations of two goods providing equal utility to the consumer. Utility is then a device to represent preferences rather than something from which preferences come. The main use of indifference curves is in the representation of potentially observable demand patterns for individual consumers over commodity bundles. There are infinitely many indifference curves: on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |