|
McCay Cubic
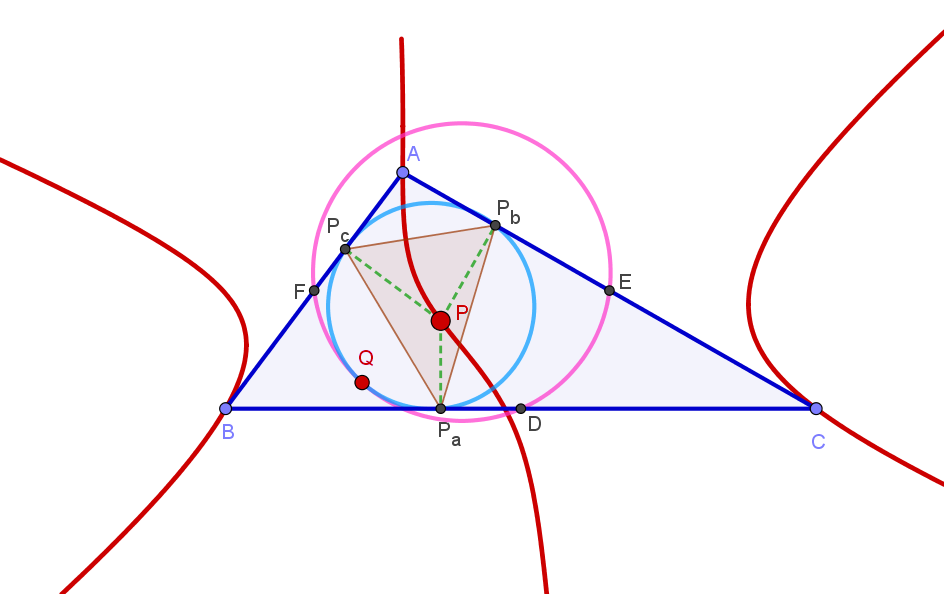
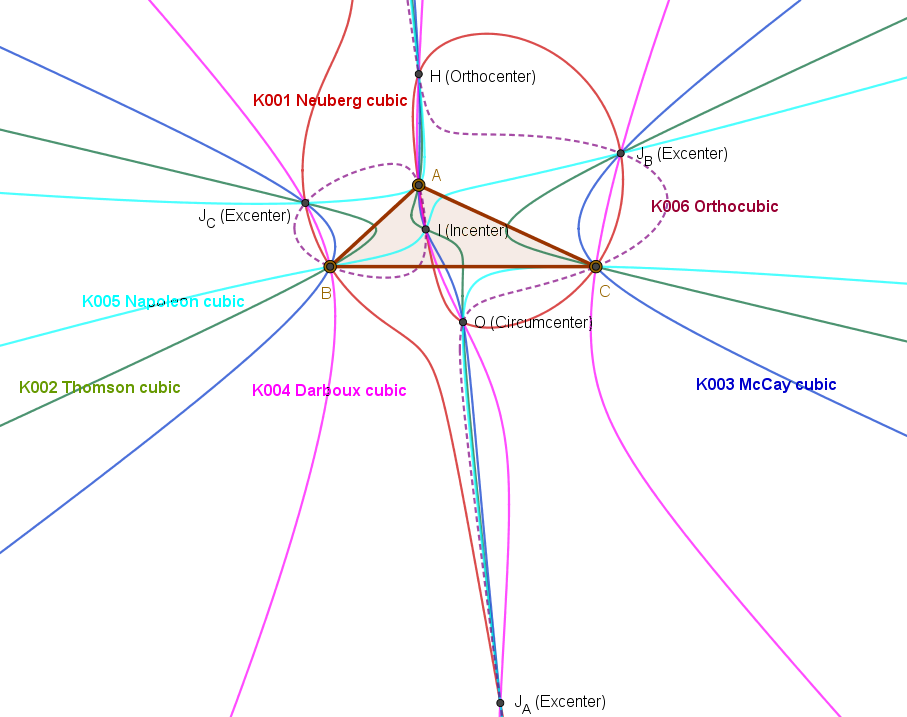
In Euclidean geometry, the McCay cubic (also called M'Cay cubic or Griffiths cubic) is a cubic plane curve in the plane of a reference triangle and associated with it. It is the third cubic curve in Bernard Gilbert's Catalogue of Triangle Cubics and it is assigned the identification number K003. Definition The McCay cubic can be defined by locus properties in several ways. For example, the McCay cubic is the locus of a point such that the pedal circle of is tangent to the nine-point circle of the reference triangle . The McCay cubic can also be defined as the locus of point such that the circumcevian triangle of and are orthologic. Equation of the McCay cubic The equation of the McCay cubic in barycentric coordinates x:y:z is :\sum_(a^2(b^2+c^2-a^2)x(c^2y^2-b^2z^2))=0. The equation in trilinear coordinates \alpha : \beta : \gamma is :\alpha (\beta^2 - \gamma^2)\cos A + \beta (\gamma^2 - \alpha^2)\cos B + \gamma (\alpha^2 - \beta^2)\cos C = 0 McCay cubic as a stelloid A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematics, Greek mathematician Euclid, which he described in his textbook on geometry: the ''Euclid's Elements, Elements''. Euclid's approach consists in assuming a small set of intuitively appealing axioms (postulates) and deducing many other propositions (theorems) from these. Although many of Euclid's results had been stated earlier,. Euclid was the first to organize these propositions into a logic, logical system in which each result is ''mathematical proof, proved'' from axioms and previously proved theorems. The ''Elements'' begins with plane geometry, still taught in secondary school (high school) as the first axiomatic system and the first examples of mathematical proofs. It goes on to the solid geometry of three dimensions. Much of the ''Elements'' states results of what are now called algebra and number theory, explained in geometrical language. For more than two thousand years, the adjective " ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cubic Plane Curve
In mathematics, a cubic plane curve is a plane algebraic curve defined by a cubic equation : applied to homogeneous coordinates for the projective plane; or the inhomogeneous version for the affine space determined by setting in such an equation. Here is a non-zero linear combination of the third-degree monomials : These are ten in number; therefore the cubic curves form a projective space of dimension 9, over any given field . Each point imposes a single linear condition on , if we ask that pass through . Therefore, we can find some cubic curve through any nine given points, which may be degenerate, and may not be unique, but will be unique and non-degenerate if the points are in general position; compare to two points determining a line and how five points determine a conic. If two cubics pass through a given set of nine points, then in fact a pencil of cubics does, and the points satisfy additional properties; see Cayley–Bacharach theorem. A cubic curve may ha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangle
A triangle is a polygon with three Edge (geometry), edges and three Vertex (geometry), vertices. It is one of the basic shapes in geometry. A triangle with vertices ''A'', ''B'', and ''C'' is denoted \triangle ABC. In Euclidean geometry, any three points, when non-Collinearity, collinear, determine a unique triangle and simultaneously, a unique Plane (mathematics), plane (i.e. a two-dimensional Euclidean space). In other words, there is only one plane that contains that triangle, and every triangle is contained in some plane. If the entire geometry is only the Euclidean plane, there is only one plane and all triangles are contained in it; however, in higher-dimensional Euclidean spaces, this is no longer true. This article is about triangles in Euclidean geometry, and in particular, the Euclidean plane, except where otherwise noted. Types of triangle The terminology for categorizing triangles is more than two thousand years old, having been defined on the very first page of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Catalogue Of Triangle Cubics
The Catalogue of Triangle Cubics is an online resource containing detailed information about more than 1200 cubic curves in the plane of a reference triangle. The resource is maintained by Bernard Gilbert. Each cubic in the resource is assigned a unique identification number of the form "Knnn" where "nnn" denotes three digits. The identification number of the first entry in the catalogue is "K001" which is the Neuberg cubic of the reference triangle . The catalogue provides, among other things, the following information about each of the cubics listed: * Barycentric equation of the curve *A list of triangle centers which lie on the curve *Special points on the curve which are not triangle centers *Geometric properties of the curve *Locus properties of the curve *Other special properties of the curve *Other curves related to the cubic curve *Plenty of neat and tidy figures illustrating the various properties *References to literature on the curve The equations of some of the cubics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Locus (mathematics)
In geometry, a locus (plural: ''loci'') (Latin word for "place", "location") is a set of all points (commonly, a line, a line segment, a curve or a surface), whose location satisfies or is determined by one or more specified conditions.. In other words, the set of the points that satisfy some property is often called the ''locus of a point'' satisfying this property. The use of the singular in this formulation is a witness that, until the end of the 19th century, mathematicians did not consider infinite sets. Instead of viewing lines and curves as sets of points, they viewed them as places where a point may be ''located'' or may move. History and philosophy Until the beginning of the 20th century, a geometrical shape (for example a curve) was not considered as an infinite set of points; rather, it was considered as an entity on which a point may be located or on which it moves. Thus a circle in the Euclidean plane was defined as the ''locus'' of a point that is at a given dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tangent
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. More precisely, a straight line is said to be a tangent of a curve at a point if the line passes through the point on the curve and has slope , where ''f'' is the derivative of ''f''. A similar definition applies to space curves and curves in ''n''-dimensional Euclidean space. As it passes through the point where the tangent line and the curve meet, called the point of tangency, the tangent line is "going in the same direction" as the curve, and is thus the best straight-line approximation to the curve at that point. The tangent line to a point on a differentiable curve can also be thought of as a '' tangent line approximation'', the graph of the affine function that best approximates the original function at the given point. Similarly, t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circumcevian Triangle
In triangle geometry, a circumcevian triangle is a special triangle associated with the reference triangle and a point in the plane of the triangle. It is also associated with the circumcircle of the reference triangle. Definition Let P be a point in the plane of the reference triangle ABC. Let the lines AP, BP, CP intersect the circumcircle of triangle ABC at A', B', C'. The triangle A'B'C' is called the circumcevian triangle of P with reference to the triangle ABC. Coordinates Let a,b,c be the side lengths of triangle ABC and let the trilinear coordinates of P be \alpha:\beta:\gamma. Then the trilinear coordinates of the vertices of the circumcevian triangle of P are as follows: :A' (-a\beta\gamma : (b\gamma+c\beta)\beta : (b\gamma+c\beta)\gamma) :B' ((c\alpha +a\gamma)\alpha : - b\gamma\alpha : (c\alpha +a\gamma) \gamma) :C' ((a\beta +b\alpha)\alpha : (a\beta +b\alpha)\beta : - c\alpha\beta) Some properties *Every triangle inscribed in the circumcircle of the reference triangle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthologic Triangles
In geometry, two triangles are said to be orthologic if the perpendiculars from the vertices of one of them to the corresponding sides of the other are concurrent (i.e., they intersect at a single point). This is a symmetric property; that is, if the perpendiculars from the vertices of triangle to the sides of triangle are concurrent then the perpendiculars from the vertices of to the sides of are also concurrent. The points of concurrence are known as the orthology centres of the two triangles. Some pairs of orthologic triangles The following are some triangles associated with the reference triangle ABC and orthologic with it. * Medial triangle * Anticomplementary triangle * Orthic triangle * The triangle whose vertices are the points of contact of the incircle with the sides of ABC * Tangential triangle * The triangle whose vertices are the points of contacts of the excircles with the respective sides of triangle ABC * The triangle formed by the bisectors of the exte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Barycentric Coordinate System
In geometry, a barycentric coordinate system is a coordinate system in which the location of a point is specified by reference to a simplex (a triangle for points in a plane, a tetrahedron for points in three-dimensional space, etc.). The barycentric coordinates of a point can be interpreted as masses placed at the vertices of the simplex, such that the point is the center of mass (or ''barycenter'') of these masses. These masses can be zero or negative; they are all positive if and only if the point is inside the simplex. Every point has barycentric coordinates, and their sum is not zero. Two tuples of barycentric coordinates specify the same point if and only if they are proportional; that is to say, if one tuple can be obtained by multiplying the elements of the other tuple by the same non-zero number. Therefore, barycentric coordinates are either considered to be defined up to multiplication by a nonzero constant, or normalized for summing to unity. Barycentric coordinates ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trilinear Coordinates
In geometry, the trilinear coordinates of a point relative to a given triangle describe the relative directed distances from the three sidelines of the triangle. Trilinear coordinates are an example of homogeneous coordinates. The ratio is the ratio of the perpendicular distances from the point to the sides (extended if necessary) opposite vertices and respectively; the ratio is the ratio of the perpendicular distances from the point to the sidelines opposite vertices and respectively; and likewise for and vertices and . In the diagram at right, the trilinear coordinates of the indicated interior point are the actual distances (, , ), or equivalently in ratio form, for any positive constant . If a point is on a sideline of the reference triangle, its corresponding trilinear coordinate is 0. If an exterior point is on the opposite side of a sideline from the interior of the triangle, its trilinear coordinate associated with that sideline is negative. It is impossible ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |