|
Mathematics Of Sudoku
The mathematics of Sudoku refers to the use of mathematics to study Sudoku puzzles to answer questions such as ''"How many filled Sudoku grids are there?"'', "''What is the minimal number of clues in a valid puzzle?''" and ''"In what ways can Sudoku grids be symmetric?"'' through the use of combinatorics and group theory. The analysis of Sudoku falls is generally divided between analyzing the properties of unsolved puzzles (such as the minimum possible number of given clues) and analyzing the properties of solved puzzles. Initial analysis was largely focused on enumerating solutions, with results first appearing in 2004. For classical Sudoku, the number of filled grids is 6,670,903,752,021,072,936,960 (), which reduces to 5,472,730,538 essentially different solutions under the validity preserving transformations. There are 26 types of symmetry, but they can only be found in about 0.005% of all filled grids. A puzzle with a unique solution must have at least 17 clues, and the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sudoku Puzzle (automorphic With Translational Symmetry)
Sudoku (; ja, 数独, sūdoku, digit-single; originally called Number Place) is a logic-based, combinatorial number-placement puzzle. In classic Sudoku, the objective is to fill a 9 × 9 grid with digits so that each column, each row, and each of the nine 3 × 3 subgrids that compose the grid (also called "boxes", "blocks", or "regions") contain all of the digits from 1 to 9. The puzzle setter provides a partially completed grid, which for a well-posed puzzle has a single solution. French newspapers featured variations of the Sudoku puzzles in the 19th century, and the puzzle has appeared since 1979 in puzzle books under the name Number Place. However, the modern Sudoku only began to gain widespread popularity in 1986 when it was published by the Japanese puzzle company Nikoli under the name Sudoku, meaning "single number". It first appeared in a U.S. newspaper, and then ''The Times'' (London), in 2004, thanks to the efforts of Wayne Gould, who devised a com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
NP-complete
In computational complexity theory, a problem is NP-complete when: # it is a problem for which the correctness of each solution can be verified quickly (namely, in polynomial time) and a brute-force search algorithm can find a solution by trying all possible solutions. # the problem can be used to simulate every other problem for which we can verify quickly that a solution is correct. In this sense, NP-complete problems are the hardest of the problems to which solutions can be verified quickly. If we could find solutions of some NP-complete problem quickly, we could quickly find the solutions of every other problem to which a given solution can be easily verified. The name "NP-complete" is short for "nondeterministic polynomial-time complete". In this name, "nondeterministic" refers to nondeterministic Turing machines, a way of mathematically formalizing the idea of a brute-force search algorithm. Polynomial time refers to an amount of time that is considered "quick" for a det ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Permutation
In mathematics, a permutation of a set is, loosely speaking, an arrangement of its members into a sequence or linear order, or if the set is already ordered, a rearrangement of its elements. The word "permutation" also refers to the act or process of changing the linear order of an ordered set. Permutations differ from combinations, which are selections of some members of a set regardless of order. For example, written as tuples, there are six permutations of the set , namely (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), and (3, 2, 1). These are all the possible orderings of this three-element set. Anagrams of words whose letters are different are also permutations: the letters are already ordered in the original word, and the anagram is a reordering of the letters. The study of permutations of finite sets is an important topic in the fields of combinatorics and group theory. Permutations are used in almost every branch of mathematics, and in many other fields of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
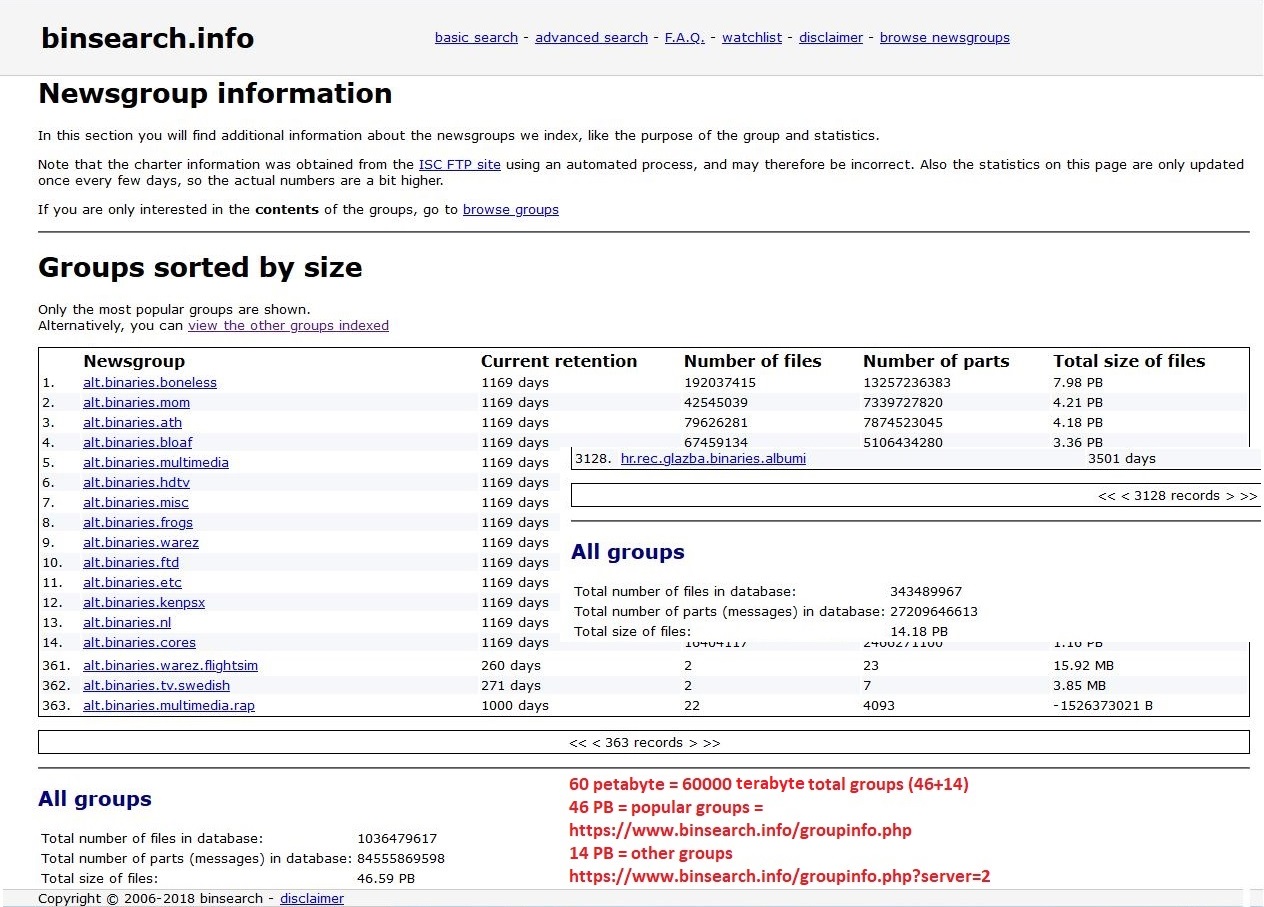
Newsgroup
A Usenet newsgroup is a repository usually within the Usenet system, for messages posted from users in different locations using the Internet. They are discussion groups and are not devoted to publishing news. Newsgroups are technically distinct from, but functionally similar to, discussion forums on the World Wide Web. Newsreader software is used to read the content of newsgroups. Before the adoption of the World Wide Web, Usenet newsgroups were among the most popular Internet services, and have retained their noncommercial nature in contrast to the increasingly ad-laden web. In recent years, this form of open discussion on the Internet has lost considerable ground to individually-operated browser-accessible forums and big media social networks such as Facebook and Twitter. Communication is facilitated by the Network News Transfer Protocol (NNTP) which allows connection to Usenet servers and data transfer over the internet. Similar to another early (yet still used) prot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polyomino
A polyomino is a plane geometric figure formed by joining one or more equal squares edge to edge. It is a polyform whose cells are squares. It may be regarded as a finite subset of the regular square tiling. Polyominoes have been used in popular puzzles since at least 1907, and the enumeration of pentominoes is dated to antiquity. Many results with the pieces of 1 to 6 squares were first published in '' Fairy Chess Review'' between the years 1937 to 1957, under the name of "dissection problems." The name ''polyomino'' was invented by Solomon W. Golomb in 1953, and it was popularized by Martin Gardner in a November 1960 "Mathematical Games" column in ''Scientific American''. Related to polyominoes are polyiamonds, formed from equilateral triangles; polyhexes, formed from regular hexagons; and other plane polyforms. Polyominoes have been generalized to higher dimensions by joining cubes to form polycubes, or hypercubes to form polyhypercubes. In statistical physics, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exact Sequence
An exact sequence is a sequence of morphisms between objects (for example, groups, rings, modules, and, more generally, objects of an abelian category) such that the image of one morphism equals the kernel of the next. Definition In the context of group theory, a sequence :G_0\;\xrightarrow\; G_1 \;\xrightarrow\; G_2 \;\xrightarrow\; \cdots \;\xrightarrow\; G_n of groups and group homomorphisms is said to be exact at G_i if \operatorname(f_i)=\ker(f_). The sequence is called exact if it is exact at each G_i for all 1\leq i |
Group Homomorphism
In mathematics, given two groups, (''G'', ∗) and (''H'', ·), a group homomorphism from (''G'', ∗) to (''H'', ·) is a function ''h'' : ''G'' → ''H'' such that for all ''u'' and ''v'' in ''G'' it holds that : h(u*v) = h(u) \cdot h(v) where the group operation on the left side of the equation is that of ''G'' and on the right side that of ''H''. From this property, one can deduce that ''h'' maps the identity element ''eG'' of ''G'' to the identity element ''eH'' of ''H'', : h(e_G) = e_H and it also maps inverses to inverses in the sense that : h\left(u^\right) = h(u)^. \, Hence one can say that ''h'' "is compatible with the group structure". Older notations for the homomorphism ''h''(''x'') may be ''x''''h'' or ''x''''h'', though this may be confused as an index or a general subscript. In automata theory, sometimes homomorphisms are written to the right of their arguments without parentheses, so that ''h''(''x'') becomes simply xh. In areas of mathematics where o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quotient Group
A quotient group or factor group is a mathematical group obtained by aggregating similar elements of a larger group using an equivalence relation that preserves some of the group structure (the rest of the structure is "factored" out). For example, the cyclic group of addition modulo ''n'' can be obtained from the group of integers under addition by identifying elements that differ by a multiple of n and defining a group structure that operates on each such class (known as a congruence class) as a single entity. It is part of the mathematical field known as group theory. For a congruence relation on a group, the equivalence class of the identity element is always a normal subgroup of the original group, and the other equivalence classes are precisely the cosets of that normal subgroup. The resulting quotient is written G\,/\,N, where G is the original group and N is the normal subgroup. (This is pronounced G\bmod N, where \mbox is short for modulo.) Much of the importan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Subgroup
In group theory, a branch of mathematics, given a group ''G'' under a binary operation ∗, a subset ''H'' of ''G'' is called a subgroup of ''G'' if ''H'' also forms a group under the operation ∗. More precisely, ''H'' is a subgroup of ''G'' if the restriction of ∗ to is a group operation on ''H''. This is often denoted , read as "''H'' is a subgroup of ''G''". The trivial subgroup of any group is the subgroup consisting of just the identity element. A proper subgroup of a group ''G'' is a subgroup ''H'' which is a proper subset of ''G'' (that is, ). This is often represented notationally by , read as "''H'' is a proper subgroup of ''G''". Some authors also exclude the trivial group from being proper (that is, ). If ''H'' is a subgroup of ''G'', then ''G'' is sometimes called an overgroup of ''H''. The same definitions apply more generally when ''G'' is an arbitrary semigroup, but this article will only deal with subgroups of groups. Subgroup tests Suppose ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cayley Table
Named after the 19th century British mathematician Arthur Cayley, a Cayley table describes the structure of a finite group by arranging all the possible products of all the group's elements in a square table reminiscent of an addition or multiplication table. Many properties of a groupsuch as whether or not it is abelian, which elements are inverses of which elements, and the size and contents of the group's centercan be discovered from its Cayley table. A simple example of a Cayley table is the one for the group under ordinary multiplication: History Cayley tables were first presented in Cayley's 1854 paper, "On The Theory of Groups, as depending on the symbolic equation ''θ'' ''n'' = 1". In that paper they were referred to simply as tables, and were merely illustrativethey came to be known as Cayley tables later on, in honour of their creator. Structure and layout Because many Cayley tables describe groups that are not abelian, the product ''ab'' with respect t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multiplication Table
In mathematics, a multiplication table (sometimes, less formally, a times table) is a mathematical table used to define a multiplication operation for an algebraic system. The decimal multiplication table was traditionally taught as an essential part of elementary arithmetic around the world, as it lays the foundation for arithmetic operations with base-ten numbers. Many educators believe it is necessary to memorize the table up to 9 × 9. History In pre-modern time The oldest known multiplication tables were used by the Babylonians about 4000 years ago. However, they used a base of 60. The oldest known tables using a base of 10 are the Chinese decimal multiplication table on bamboo strips dating to about 305 BC, during China's Warring States period. The multiplication table is sometimes attributed to the ancient Greek mathematician Pythagoras (570–495 BC). It is also called the Table of Pythagoras in many languages (for example French, Italian and Russian) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Latin Square
In combinatorics and in experimental design, a Latin square is an ''n'' × ''n'' array filled with ''n'' different symbols, each occurring exactly once in each row and exactly once in each column. An example of a 3×3 Latin square is The name "Latin square" was inspired by mathematical papers by Leonhard Euler (1707–1783), who used Latin characters as symbols, but any set of symbols can be used: in the above example, the alphabetic sequence A, B, C can be replaced by the integer sequence 1, 2, 3. Euler began the general theory of Latin squares. History The Korean mathematician Choi Seok-jeong was the first to publish an example of Latin squares of order nine, in order to construct a magic square in 1700, predating Leonhard Euler by 67 years. Reduced form A Latin square is said to be ''reduced'' (also, ''normalized'' or ''in standard form'') if both its first row and its first column are in their natural order. For example, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.png)