|
Marcum Q-function
In statistics, the generalized Marcum Q-function of order \nu is defined as : Q_\nu (a,b) = \frac \int_b^\infty x^\nu \exp \left( -\frac \right) I_(ax) \, dx where b \geq 0 and a, \nu > 0 and I_ is the modified Bessel function of first kind of order \nu-1. If b > 0, the integral converges for any \nu. The Marcum Q-function occurs as a complementary cumulative distribution function for noncentral chi, noncentral chi-squared, and Rice distributions. In engineering, this function appears in the study of radar systems, communication systems, queueing system, and signal processing. This function was first studied for \nu = 1, and hence named after, by Jess Marcum for pulsed radars.J.I. Marcum (1960). A statistical theory of target detection by pulsed radar: mathematical appendix, ''IRE Trans. Inform. Theory,'' vol. 6, 59-267. Properties Finite integral representation The generalized Marcum Q-function can alternatively be defined as a finite integral as : Q_\nu (a,b) = 1 - \frac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German: '' Statistik'', "description of a state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample to the population as a whole. An ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Erlang Distribution
The Erlang distribution is a two-parameter family of continuous probability distributions with support x \in exponential distribution">exponential variables with mean 1/\lambda each. Equivalently, it is the distribution of the time until the ''k''th event of a Poisson process with a rate of \lambda. The Erlang and Poisson distributions are complementary, in that while the Poisson distribution counts the number of events that occur in a fixed amount of time, the Erlang distribution counts the amount of time until the occurrence of a fixed number of events. When k=1, the distribution simplifies to the exponential distribution. The Erlang distribution is a special case of the gamma distribution wherein the shape of the distribution is discretised. The Erlang distribution was developed by Agner Krarup Erlang, A. K. Erlang to examine the number of telephone calls which might be made at the same time to the operators of the switching stations. This work on telephone Teletraffic en ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nakagami Distribution
The Nakagami distribution or the Nakagami-''m'' distribution is a probability distribution related to the gamma distribution. The family of Nakagami distributions has two parameters: a shape parameter m\geq 1/2 and a second parameter controlling spread \Omega>0. Characterization Its probability density function (pdf) is : f(x;\,m,\Omega) = \fracx^\exp\left(-\fracx^2\right), \forall x\geq 0. where (m\geq 1/2,\text\Omega>0) Its cumulative distribution function is : F(x;\,m,\Omega) = P\left(m, \fracx^2\right) where ''P'' is the regularized (lower) incomplete gamma function. Parametrization The parameters m and \Omega are : m = \frac , and : \Omega = \operatorname \left ^2 \right Parameter estimation An alternative way of fitting the distribution is to re-parametrize \Omega and ''m'' as ''σ'' = Ω/''m'' and ''m''. Given independent observations X_1=x_1,\ldots,X_n=x_n from the Nakagami distribution, the likelihood function is : L( \si ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chi Distribution
In probability theory and statistics, the chi distribution is a continuous probability distribution. It is the distribution of the positive square root of the sum of squares of a set of independent random variables each following a standard normal distribution, or equivalently, the distribution of the Euclidean distance of the random variables from the origin. It is thus related to the chi-squared distribution by describing the distribution of the positive square roots of a variable obeying a chi-squared distribution. If Z_1, \ldots, Z_k are k independent, normally distributed random variables with mean 0 and standard deviation 1, then the statistic :Y = \sqrt is distributed according to the chi distribution. The chi distribution has one parameter, k, which specifies the number of degrees of freedom (i.e. the number of random variables Z_i). The most familiar examples are the Rayleigh distribution (chi distribution with two degrees of freedom) and the Maxwell–Boltzman ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maxwell–Boltzmann Distribution
In physics (in particular in statistical mechanics), the Maxwell–Boltzmann distribution, or Maxwell(ian) distribution, is a particular probability distribution named after James Clerk Maxwell and Ludwig Boltzmann. It was first defined and used for describing particle speeds in idealized gases, where the particles move freely inside a stationary container without interacting with one another, except for very brief collisions in which they exchange energy and momentum with each other or with their thermal environment. The term "particle" in this context refers to gaseous particles only ( atoms or molecules), and the system of particles is assumed to have reached thermodynamic equilibrium.''Statistical Physics'' (2nd Edition), F. Mandl, Manchester Physics, John Wiley & Sons, 2008, The energies of such particles follow what is known as Maxwell–Boltzmann statistics, and the statistical distribution of speeds is derived by equating particle energies with kinetic energy. Mathem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rayleigh Distribution
In probability theory and statistics, the Rayleigh distribution is a continuous probability distribution for nonnegative-valued random variables. Up to rescaling, it coincides with the chi distribution with two degrees of freedom. The distribution is named after Lord Rayleigh (). A Rayleigh distribution is often observed when the overall magnitude of a vector is related to its directional components. One example where the Rayleigh distribution naturally arises is when wind velocity is analyzed in two dimensions. Assuming that each component is uncorrelated, normally distributed with equal variance, and zero mean, then the overall wind speed (vector magnitude) will be characterized by a Rayleigh distribution. A second example of the distribution arises in the case of random complex numbers whose real and imaginary components are independently and identically distributed Gaussian with equal variance and zero mean. In that case, the absolute value of the complex number is Ra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Non-central Chi-squared Distribution
In probability theory and statistics, the noncentral chi-squared distribution (or noncentral chi-square distribution, noncentral \chi^2 distribution) is a noncentral generalization of the chi-squared distribution. It often arises in the power analysis of statistical tests in which the null distribution is (perhaps asymptotically) a chi-squared distribution; important examples of such tests are the likelihood-ratio tests. Definitions Background Let (X_1,X_2, \ldots, X_i, \ldots,X_k) be ''k'' independent, normally distributed random variables with means \mu_i and unit variances. Then the random variable : \sum_^k X_i^2 is distributed according to the noncentral chi-squared distribution. It has two parameters: k which specifies the number of degrees of freedom (i.e. the number of X_i), and \lambda which is related to the mean of the random variables X_i by: : \lambda=\sum_^k \mu_i^2. \lambda is sometimes called the noncentrality parameter. Note that some references define \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalized Gamma Distribution
The generalized gamma distribution is a continuous probability distribution with two shape parameters (and a scale parameter). It is a generalization of the gamma distribution which has one shape parameter (and a scale parameter). Since many distributions commonly used for parametric models in survival analysis (such as the exponential distribution, the Weibull distribution and the gamma distribution) are special cases of the generalized gamma, it is sometimes used to determine which parametric model is appropriate for a given set of data. Another example is the half-normal distribution. Characteristics The generalized gamma distribution has two shape parameters, d > 0 and p > 0, and a scale parameter, a > 0. For non-negative ''x'' from a generalized gamma distribution, the probability density function is : f(x; a, d, p) = \frac, where \Gamma(\cdot) denotes the gamma function. The cumulative distribution function is : F(x; a, d, p) = \frac , where \gamma(\cdot) denotes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weibull Distribution
In probability theory and statistics, the Weibull distribution is a continuous probability distribution. It is named after Swedish mathematician Waloddi Weibull, who described it in detail in 1951, although it was first identified by Maurice René Fréchet and first applied by to describe a particle size distribution. Definition Standard parameterization The probability density function of a Weibull random variable is : f(x;\lambda,k) = \begin \frac\left(\frac\right)^e^, & x\geq0 ,\\ 0, & x 0 is the '' shape parameter'' and λ > 0 is the '' scale parameter'' of the distribution. Its complementary cumulative distribution function is a stretched exponential function. The Weibull distribution is related to a number of other probability distributions; in particular, it interpolates between the exponential distribution (''k'' = 1) and the Rayleigh distribution (''k'' = 2 and \lambda = \sqrt\sigma ). If the quantity ''X'' is a "time-to-failure", the Weibull distribution gives a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
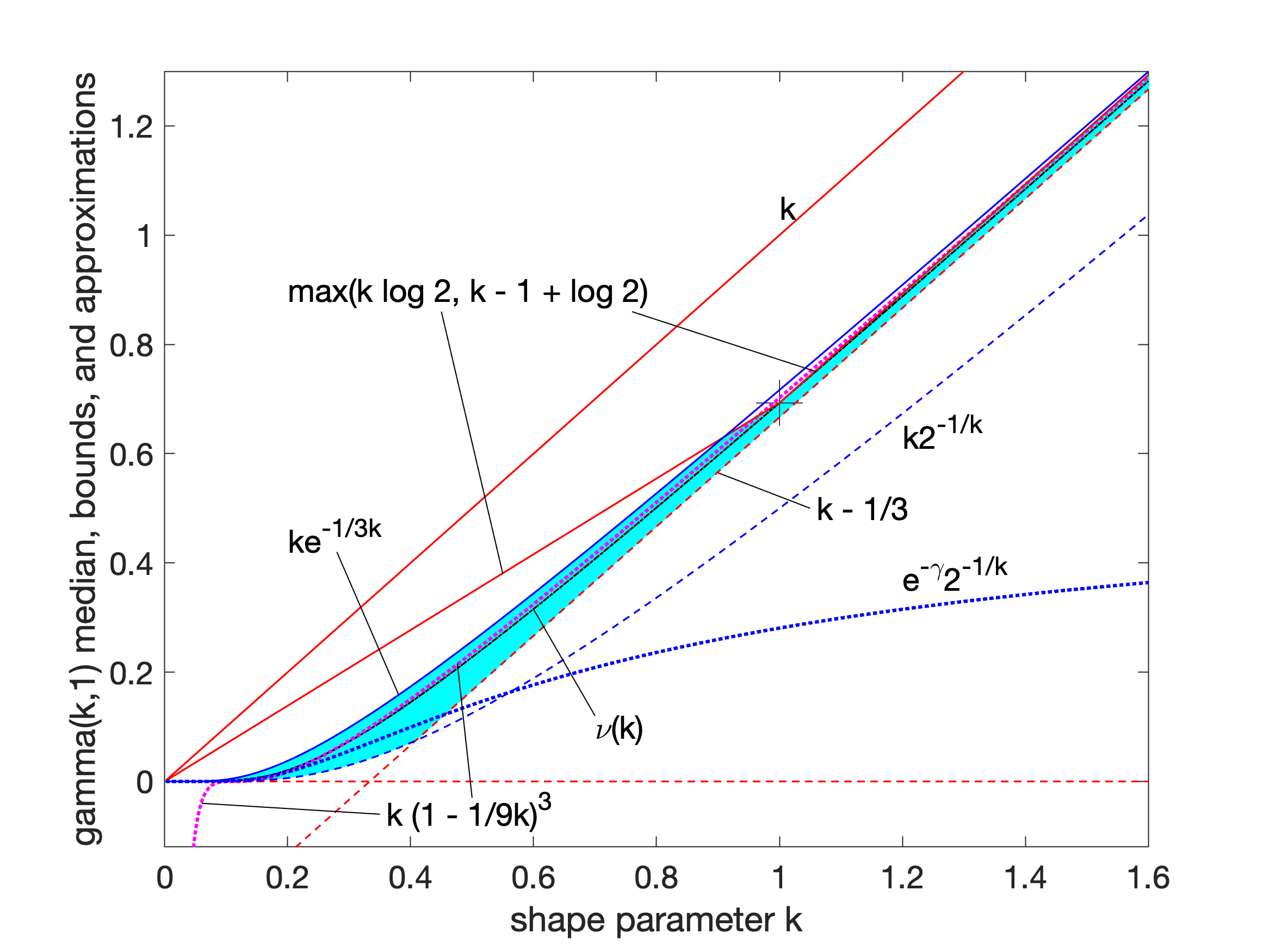
Gamma Distribution
In probability theory and statistics, the gamma distribution is a two- parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and chi-square distribution are special cases of the gamma distribution. There are two equivalent parameterizations in common use: #With a shape parameter k and a scale parameter \theta. #With a shape parameter \alpha = k and an inverse scale parameter \beta = 1/ \theta , called a rate parameter. In each of these forms, both parameters are positive real numbers. The gamma distribution is the maximum entropy probability distribution (both with respect to a uniform base measure and a 1/x base measure) for a random variable X for which E 'X''= ''kθ'' = ''α''/''β'' is fixed and greater than zero, and E n(''X'')= ''ψ''(''k'') + ln(''θ'') = ''ψ''(''α'') − ln(''β'') is fixed (''ψ'' is the digamma function). Definitions The parameterization with ''k'' and ''θ'' appears to be more common ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chi-squared Distribution
In probability theory and statistics, the chi-squared distribution (also chi-square or \chi^2-distribution) with k degrees of freedom is the distribution of a sum of the squares of k independent standard normal random variables. The chi-squared distribution is a special case of the gamma distribution and is one of the most widely used probability distributions in inferential statistics, notably in hypothesis testing and in construction of confidence intervals. This distribution is sometimes called the central chi-squared distribution, a special case of the more general noncentral chi-squared distribution. The chi-squared distribution is used in the common chi-squared tests for goodness of fit of an observed distribution to a theoretical one, the independence of two criteria of classification of qualitative data, and in confidence interval estimation for a population standard deviation of a normal distribution from a sample standard deviation. Many other statistical tes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponential Distribution
In probability theory and statistics, the exponential distribution is the probability distribution of the time between events in a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average rate. It is a particular case of the gamma distribution. It is the continuous analogue of the geometric distribution, and it has the key property of being memoryless. In addition to being used for the analysis of Poisson point processes it is found in various other contexts. The exponential distribution is not the same as the class of exponential families of distributions. This is a large class of probability distributions that includes the exponential distribution as one of its members, but also includes many other distributions, like the normal, binomial, gamma, and Poisson distributions. Definitions Probability density function The probability density function (pdf) of an exponential distribution is : f(x;\lambda) = \begin \l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |

-pdf.png)