|
Maas–Hoffman Model
The Maas–Hoffman model is a mathematical tool to characterize the relation between crop production and soil salinity. It describes the crop response by a broken line of which the first part is horizontal and the second is sloping downward.Maas EV, Hoffman GJ, 1977. ''Crop salt tolerance-current assessment''. Journal of the Irrigation and Drainage Division, American Society of Civil Engineers 103: 115-134. The ''breakpoint'' (Pb) or ''threshold'' is also called ''tolerance'' because up to that point the yield is unaffected by the salinity, so the salt is tolerated, while at greater salinity values the crops are affected negatively and the yield goes down. Mathematics Mathematically the two lines are represented by the equations: : \left\{\begin{array}{l} Y=C, & XP_{\rm b} \end{array}\right. where ''Y'' is the crop production or yield, ''C'' is the maximum yield, ''X'' is the soil salinity, ''A'' is the slope (regression coefficient) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crop Production
Agriculture or farming is the practice of cultivating plants and livestock. Agriculture was the key development in the rise of sedentary human civilization, whereby farming of domesticated species created food surpluses that enabled people to live in cities. The history of agriculture began thousands of years ago. After gathering wild grains beginning at least 105,000 years ago, nascent farmers began to plant them around 11,500 years ago. Sheep, goats, pigs and cattle were domesticated over 10,000 years ago. Plants were independently cultivated in at least 11 regions of the world. Industrial agriculture based on large-scale monoculture in the twentieth century came to dominate agricultural output, though about 2 billion people still depended on subsistence agriculture. The major agricultural products can be broadly grouped into foods, fibers, fuels, and raw materials (such as rubber). Food classes include cereals ( grains), vegetables, fruits, cooking oils, meat, milk, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Soil Salinity
Soil salinity is the salt content in the soil; the process of increasing the salt content is known as salinization. Salts occur naturally within soils and water. Salination can be caused by natural processes such as mineral weathering or by the gradual withdrawal of an ocean. It can also come about through artificial processes such as irrigation and road salt. Natural occurrence Salts are a natural component in soils and water. The ions responsible for salination are: Na+, K+, Ca2+, Mg2+ and Cl−. Over long periods of time, as soil minerals weather and release salts, these salts are flushed or leached out of the soil by drainage water in areas with sufficient precipitation. In addition to mineral weathering, salts are also deposited via dust and precipitation. Salts may accumulate in dry regions, leading to naturally saline soils. This is the case, for example, in large parts of Australia. Human practices can increase the salinity of soils by the addition of salts i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
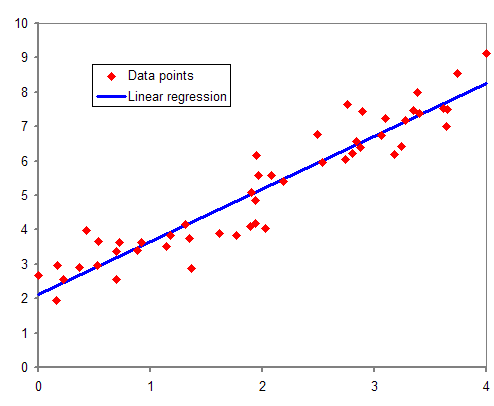
Regression Analysis
In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable (often called the 'outcome' or 'response' variable, or a 'label' in machine learning parlance) and one or more independent variables (often called 'predictors', 'covariates', 'explanatory variables' or 'features'). The most common form of regression analysis is linear regression, in which one finds the line (or a more complex linear combination) that most closely fits the data according to a specific mathematical criterion. For example, the method of ordinary least squares computes the unique line (or hyperplane) that minimizes the sum of squared differences between the true data and that line (or hyperplane). For specific mathematical reasons (see linear regression), this allows the researcher to estimate the conditional expectation (or population average value) of the dependent variable when the independent variables take on a given ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optimization
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems of sorts arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries. In the more general approach, an optimization problem consists of maximizing or minimizing a real function by systematically choosing input values from within an allowed set and computing the value of the function. The generalization of optimization theory and techniques to other formulations constitutes a large area of applied mathematics. More generally, optimization includes finding "best available" values of some objective function given a def ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Goodness Of Fit
The goodness of fit of a statistical model describes how well it fits a set of observations. Measures of goodness of fit typically summarize the discrepancy between observed values and the values expected under the model in question. Such measures can be used in statistical hypothesis testing, e.g. to normality test, test for normality of Errors and residuals in statistics, residuals, to test whether two samples are drawn from identical distributions (see Kolmogorov–Smirnov test), or whether outcome frequencies follow a specified distribution (see Pearson's chi-square test). In the analysis of variance, one of the components into which the variance is partitioned may be a lack-of-fit sum of squares. Fit of distributions In assessing whether a given distribution is suited to a data-set, the following statistical hypothesis test, tests and their underlying measures of fit can be used: *Bayesian information criterion *Kolmogorov–Smirnov test *Cramér–von Mises criterion *And ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crop Tolerance To Seawater
Crop tolerance to seawater is the ability of an agricultural crop to withstand the high salinity induced by irrigation with seawater, or a mixture of fresh water and ''seawater''. There are crops that can grow on ''seawater'' and demonstration farms have shown the feasibility. The government of the Netherlands reports a breakthrough in food security as specific varieties of potatoes, carrots, red onions, white cabbage and broccoli appear to thrive if they are irrigated with salt water. Salt Farm Texel The Salt Farm Texel, a farm on the island of Texel, The Netherlands, is testing the salt tolerance of crops under controlled field conditions. There are 56 experimental plots of 160 m2 each that are treated in eight replicas with seven different salt concentrations. These concentrations are obtained with intensive daily drip irrigations of 10 or more mm (i.e. more than 10 liter per m2 per day) with water having a salt concentration expressed in electric conductivity (EC) of 2, 4 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Watertable
The water table is the upper surface of the zone of saturation. The zone of saturation is where the pores and fractures of the ground are saturated with water. It can also be simply explained as the depth below which the ground is saturated. The water table is the surface where the water pressure head is equal to the atmospheric pressure (where gauge pressure = 0). It may be visualized as the "surface" of the subsurface materials that are saturated with groundwater in a given vicinity. The groundwater may be from precipitation or from groundwater flowing into the aquifer. In areas with sufficient precipitation, water infiltrates through pore spaces in the soil, passing through the unsaturated zone. At increasing depths, water fills in more of the pore spaces in the soils, until a zone of saturation is reached. Below the water table, in the phreatic zone (zone of saturation), layers of permeable rock that yield groundwater are called aquifers. In less permeable soils, such as t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Van Genuchten–Gupta Model
The Van Genuchten–Gupta model is an inverted S-curve applicable to crop yield and soil salinity relations.M. Th. van Genuchten and S.K. Gupta, 1993. USDA-ARS, U.S. Salinity Laboratory 4500 Glenwood Drive, Riverside, California, USA, 92501. ''A reassessment of the Crop Tolerance Response Function.'' Journal of the Indian Society of Soil Science, Vol. 41, No. 4, pp 730–737. It is named after Martinus Theodore van Genuchten and Satyandra K. Gupta's work from the 1990s. Equation The mathematical expression is: : Y = \frac where ''Y'' is the yield, ''Y''m is the maximum yield of the model, ''C'' is salt concentration of the soil, ''C''50 is the ''C'' value at 50% yield, and ''P'' is an exponent to be found by optimization and maximizing the model's goodness of fit to the data. In the figure: ''Y''m = 3.1, ''C''50 = 12.4, ''P'' = 3.75 Alternative one As an alternative, the '' logistic S-function'' can be used. The mathematical expression is: : Y^ = \frac where: : Y^ = \fra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Modeling
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used in the natural sciences (such as physics, biology, earth science, chemistry) and engineering disciplines (such as computer science, electrical engineering), as well as in non-physical systems such as the social sciences (such as economics, psychology, sociology, political science). The use of mathematical models to solve problems in business or military operations is a large part of the field of operations research. Mathematical models are also used in music, linguistics, and philosophy (for example, intensively in analytic philosophy). A model may help to explain a system and to study the effects of different components, and to make predictions about behavior. Elements of a mathematical model Mathematical models can take many forms, including dynamical systems, statistica ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crops
A crop is a plant that can be grown and harvested extensively for profit or subsistence. When the plants of the same kind are cultivated at one place on a large scale, it is called a crop. Most crops are cultivated in agriculture or hydroponics. Crops may include macroscopic fungus (e.g. mushrooms) and marine macroalga (e.g. seaweed), some of which are grown in aquaculture. Most crops are harvested as food for humans or fodder for livestock. Some crops are gathered from the wild often in a form of intensive gathering (e.g. ginseng, yohimbe, and eucommia). Important non-food crops include horticulture, floriculture and industrial crops. Horticulture crops include plants used for other crops (e.g. fruit trees). Floriculture crops include bedding plants, houseplants, flowering garden and pot plants, cut cultivated greens, and cut flowers. Industrial crops are produced for clothing (fiber crops e.g. cotton), biofuel (energy crops, algae fuel), or medicine (medicinal plants). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |