MWX Fig
MWX may refer to: * Morley–Wang–Xu element In applied mathematics, the Morlely–Wang–Xu (MWX) element is a canonical construction of a family of piecewise polynomials with the minimal degree elements for any 2m-th order of elliptic and parabolic equations in any spatial-dimension \mathb ..., a canonical construction in applied mathematics * Muan International Airport (IATA: MWX), South Jeolla Province, South Korea {{Disambiguation ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]  

Morley–Wang–Xu Element
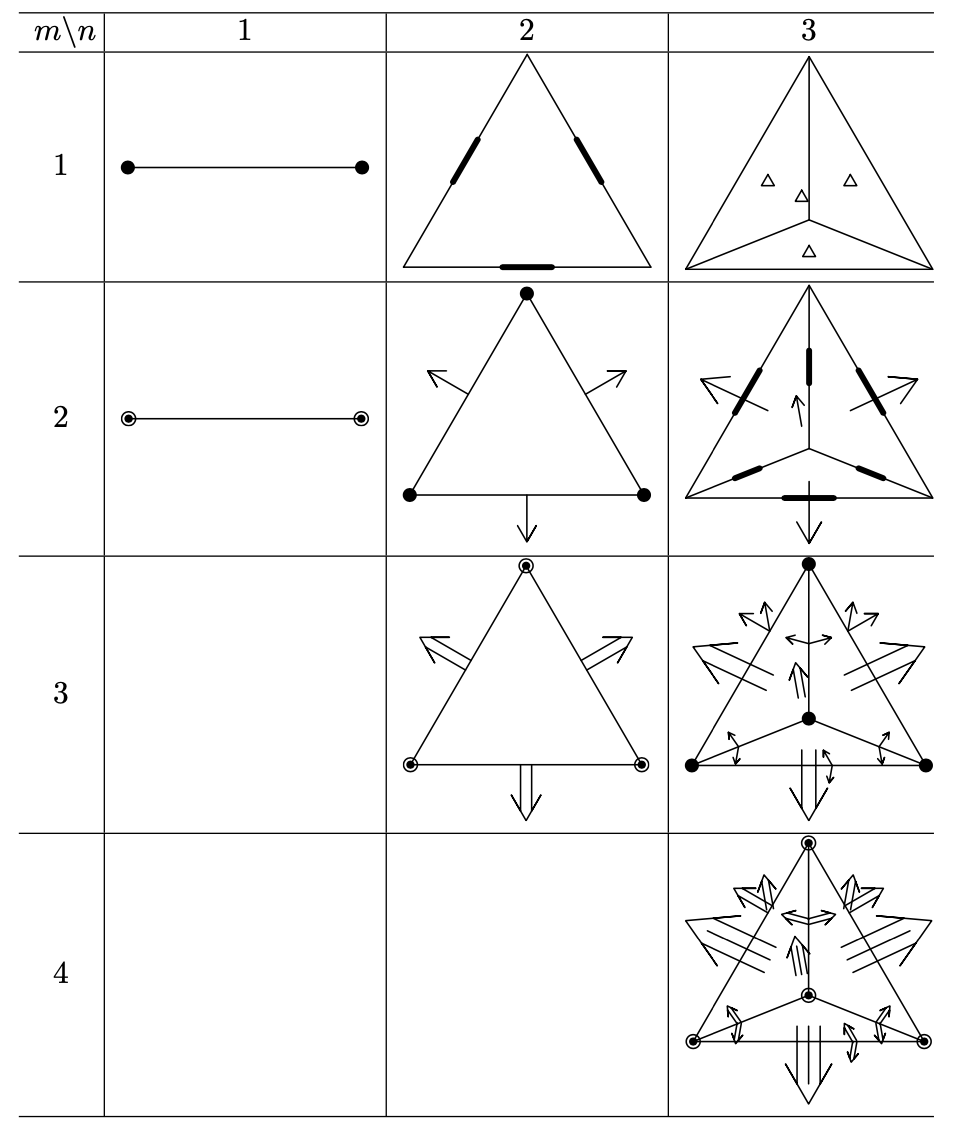
In applied mathematics, the Morlely–Wang–Xu (MWX) element is a canonical construction of a family of piecewise polynomials with the minimal degree elements for any 2m-th order of elliptic and parabolic equations in any spatial-dimension \mathbb^n for 1\leq m \leq n. The MWX element provides a consistent approximation of Sobolev space H^m in \mathbb^n. Morley–Wang–Xu element The Morley–Wang–Xu element (T,P_T,D_T) is described as follows. T is a simplex and P_T = P_m(T) . The set of degrees of freedom will be given next. Given an n-simplex T with vertices a_i, for 1\leq k\leq n, let \mathcal_ be the set consisting of all (n-k)-dimensional subsimplexe of T. For any F \in \mathcal_, let , F, denote its measure, and let \nu_, \cdots, \nu_ be its unit outer normals which are linearly independent. For 1\leq k\leq m, any (n-k)-dimensional subsimplex F\in \mathcal_ and \beta\in A_k with , \beta, =m-k, define : d_(v) = \frac\int_F \frac. The degrees of freedom are depicte ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]