Morley–Wang–Xu Element

In applied mathematics, the Morlely–Wang–Xu (MWX) element is a canonical construction of a family of piecewise polynomials with the minimal degree elements for any $2m$-th order of elliptic and parabolic equations in any spatial-dimension $\mathbb^n$ for $1\leq m \leq n$. The MWX element provides a consistent approximation of Sobolev space $H^m$ in $\mathbb^n$.

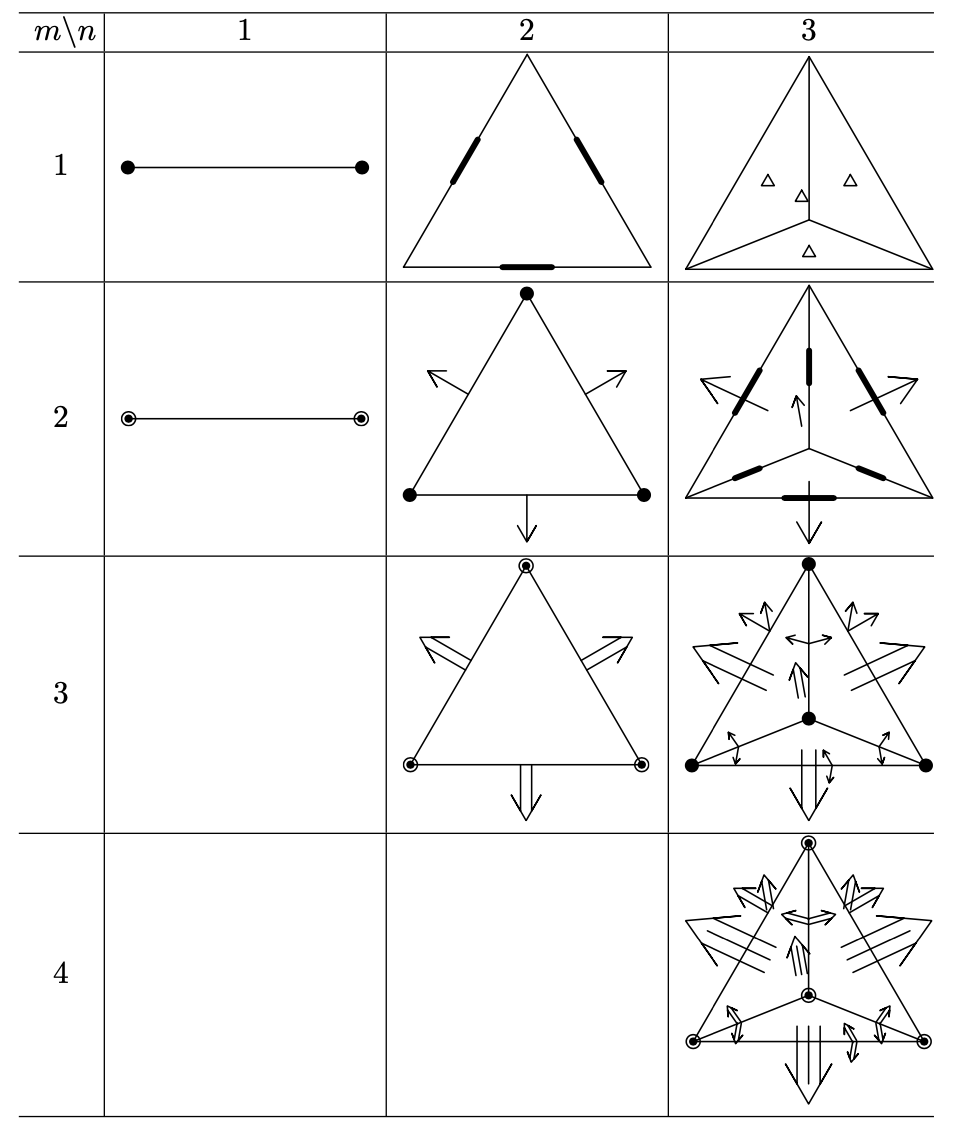
Morley–Wang–Xu element

The Morley–Wang–Xu element $(T,P_T,D_T)$ is described as follows. $T$ is a simplex and $P_T = P_m(T)$. The set of degrees of freedom will be given next.

Given an $n$-simplex $T$ with vertices $a_i$, for $1\leq k\leq n$, let $\mathcal_$ be the set consisting of all $(n-k)$-dimensional subsimplexe of $T$. For any $F \in \mathcal_$, let $, F,$ denote its measure, and let $\nu_, \cdots, \nu_$ be its unit outer normals which are linearly independent.

For $1\leq k\leq m$, any $(n-k)$-dimensional
subsimplex $F\in \mathcal_$ and $\beta\in A_k$ with $, \beta, =m-k$, define

: $d_(v) = \frac\int_F \frac.$

The degrees of freedom are depicted in Table 1. For $m=n=1$, we obtain the well-known conforming linear element. For $m=1$ and $n\geq 2$, we obtain the well-known nonconforming Crouziex–Raviart element. For $m=2$, we recover the well-known Morley element for $n=2$ and its generalization to $n\geq 2$. For $m=n=3$, we obtain a new cubic element on a simplex that has 20 degrees of freedom.

Generalizations

There are two generalizations of Morley–Wang–Xu element (which requires $1\leq m \leq n$).

$m=n+1$: Nonconforming element

As a nontrivial generalization of Morley–Wang–Xu elements, Wu and Xu propose a universal construction for the more difficult case in which $m=n+1$. Table 1 depicts the degrees of freedom for the case that $n\leq3, m\leq n+1$. The shape function space is $\mathcal_(T)+q_T\mathcal_1(T)$, where $q_T = \lambda_1\lambda_2\cdots\lambda_n+1$ is volume bubble function. This new family of finite element methods provides practical discretization methods for, say, a sixth order elliptic equations in 2D (which only has 12 local degrees of freedom). In addition, Wu and Xu propose an $H^3$ nonconforming finite element that is robust for the sixth order singularly perturbed problems in 2D.

$m,n \geq 1$: Interior penalty nonconforming FEMs

An alternative generalization when $m > n$ is developed by combining the interior penalty and nonconforming methods by Wu and Xu. This family of finite element space consists of piecewise polynomials of degree not greater than $m$. The degrees of freedom are carefully designed to preserve the weak-continuity as much as possible. For the case in which $m>n$, the corresponding interior penalty terms are applied to obtain the convergence property. As a simple example, the proposed method for the case in which $m = 3, n = 2$ is to find $u_h\in V_h$, such that

:
(\nabla^3_h u_h, \nabla^3_h v_h) + \eta \sum_ h_F^\int_F _hv_h] = (f,v_h) \quad \forall v_h \in V_h,

where the nonconforming element is depicted in Figure 1. .

References

{{DEFAULTSORT:Morley-Wang-Xu element
Polynomials