|
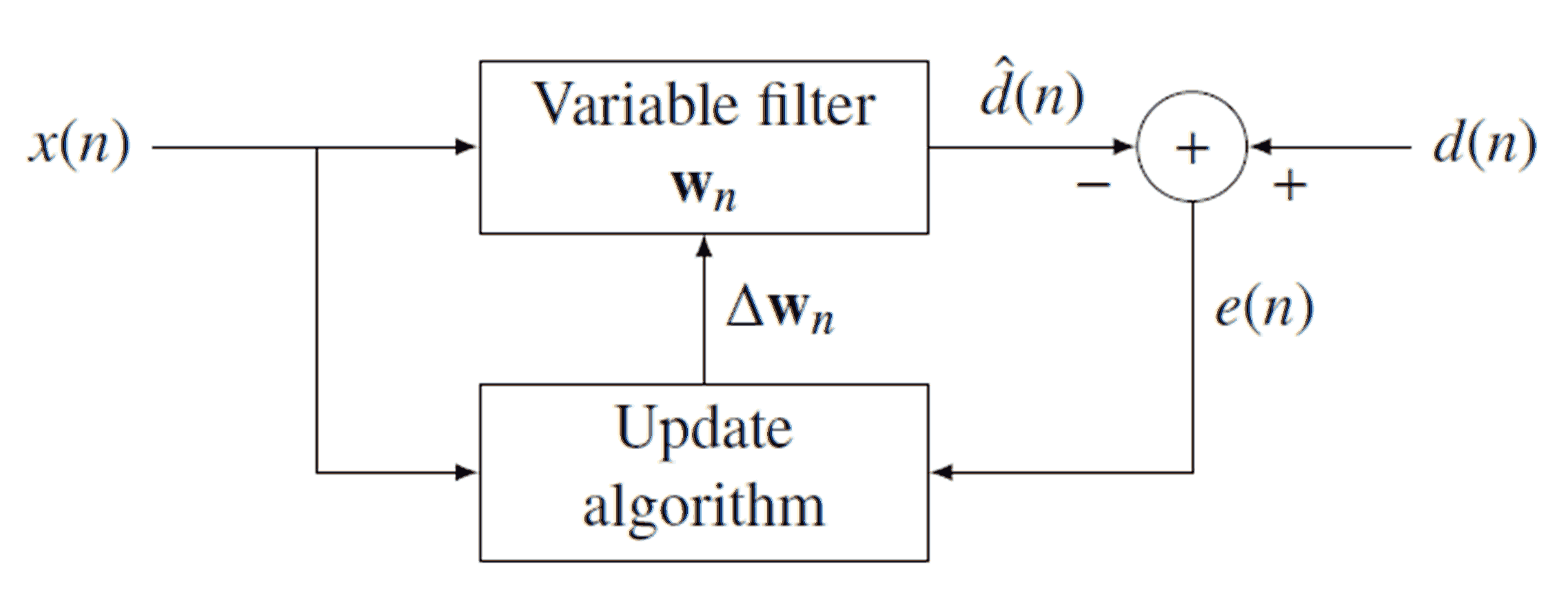
Least Mean Squares Filter
Least mean squares (LMS) algorithms are a class of adaptive filter used to mimic a desired filter by finding the filter coefficients that relate to producing the least mean square of the error signal (difference between the desired and the actual signal). It is a stochastic gradient descent method in that the filter is only adapted based on the error at the current time. It was invented in 1960 by Stanford University professor Bernard Widrow and his first Ph.D. student, Ted Hoff. Problem formulation Relationship to the Wiener filter The realization of the causal Wiener filter looks a lot like the solution to the least squares estimate, except in the signal processing domain. The least squares solution, for input matrix \mathbf and output vector \boldsymbol y is : \boldsymbol = (\mathbf ^\mathbf\mathbf)^\mathbf^\boldsymbol y . The FIR least mean squares filter is related to the Wiener filter, but minimizing the error criterion of the former does not rely on cross-corr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adaptive Filter
An adaptive filter is a system with a linear filter that has a transfer function controlled by variable parameters and a means to adjust those parameters according to an optimization algorithm. Because of the complexity of the optimization algorithms, almost all adaptive filters are digital filters. Adaptive filters are required for some applications because some parameters of the desired processing operation (for instance, the locations of reflective surfaces in a reverberant space) are not known in advance or are changing. The closed loop adaptive filter uses feedback in the form of an error signal to refine its transfer function. Generally speaking, the closed loop adaptive process involves the use of a cost function, which is a criterion for optimum performance of the filter, to feed an algorithm, which determines how to modify filter transfer function to minimize the cost on the next iteration. The most common cost function is the mean square of the error signal. As the pow ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Autocorrelation
Autocorrelation, sometimes known as serial correlation in the discrete time case, is the correlation of a signal with a delayed copy of itself as a function of delay. Informally, it is the similarity between observations of a random variable as a function of the time lag between them. The analysis of autocorrelation is a mathematical tool for finding repeating patterns, such as the presence of a periodic signal obscured by noise, or identifying the missing fundamental frequency in a signal implied by its harmonic frequencies. It is often used in signal processing for analyzing functions or series of values, such as time domain signals. Different fields of study define autocorrelation differently, and not all of these definitions are equivalent. In some fields, the term is used interchangeably with autocovariance. Unit root processes, trend-stationary processes, autoregressive processes, and moving average processes are specific forms of processes with autocorrelation. A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Digital Signal Processing
Digital signal processing (DSP) is the use of digital processing, such as by computers or more specialized digital signal processors, to perform a wide variety of signal processing operations. The digital signals processed in this manner are a sequence of numbers that represent samples of a continuous variable in a domain such as time, space, or frequency. In digital electronics, a digital signal is represented as a pulse train, which is typically generated by the switching of a transistor. Digital signal processing and analog signal processing are subfields of signal processing. DSP applications include audio and speech processing, sonar, radar and other sensor array processing, spectral density estimation, statistical signal processing, digital image processing, data compression, video coding, audio coding, image compression, signal processing for telecommunications, control systems, biomedical engineering, and seismology, among others. DSP can involve linear or nonli ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matched Filter
In signal processing, a matched filter is obtained by correlating a known delayed signal, or ''template'', with an unknown signal to detect the presence of the template in the unknown signal. This is equivalent to convolving the unknown signal with a conjugated time-reversed version of the template. The matched filter is the optimal linear filter for maximizing the signal-to-noise ratio (SNR) in the presence of additive stochastic noise. Matched filters are commonly used in radar, in which a known signal is sent out, and the reflected signal is examined for common elements of the out-going signal. Pulse compression is an example of matched filtering. It is so called because the impulse response is matched to input pulse signals. Two-dimensional matched filters are commonly used in image processing, e.g., to improve the SNR of X-ray observations. Matched filtering is a demodulation technique with LTI (linear time invariant) filters to maximize SNR. It was originally also known a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kernel Adaptive Filter
In signal processing, a kernel adaptive filter is a type of nonlinear adaptive filter. An adaptive filter is a filter that adapts its transfer function to changes in signal properties over time by minimizing an error or loss function that characterizes how far the filter deviates from ideal behavior. The adaptation process is based on learning from a sequence of signal samples and is thus an online algorithm. A nonlinear adaptive filter is one in which the transfer function is nonlinear. Kernel adaptive filters implement a nonlinear transfer function using kernel methods. In these methods, the signal is mapped to a high-dimensional linear feature space and a nonlinear function is approximated as a sum over kernels, whose domain is the feature space. If this is done in a reproducing kernel Hilbert space, a kernel method can be a universal approximator for a nonlinear function. Kernel methods have the advantage of having convex loss functions, with no local minima, and of being only ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zero-forcing Equalizer
The zero-forcing equalizer is a form of linear equalization algorithm used in communication systems which applies the inverse of the frequency response of the channel. This form of equalizer was first proposed by Robert Lucky. The zero-forcing equalizer applies the inverse of the channel frequency response to the received signal, to restore the signal after the channel. It has many useful applications. For example, it is studied heavily for IEEE 802.11n (MIMO) where knowing the channel allows recovery of the two or more streams which will be received on top of each other on each antenna. The name ''zero-forcing corresponds'' to bringing down the intersymbol interference (ISI) to zero in a noise-free case. This will be useful when ISI is significant compared to noise. For a channel with frequency response F(f) the zero-forcing equalizer C(f) is constructed by C(f) = 1/F(f). Thus the combination of channel and equalizer gives a flat frequency response and linear phase F(f)C(f) = 1. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multidelay Block Frequency Domain Adaptive Filter
The multidelay block frequency domain adaptive filter (MDF) algorithm is a block-based frequency domain implementation of the (normalised) Least mean squares filter (LMS) algorithm. Introduction The MDF algorithm is based on the fact that convolutions may be efficiently computed in the frequency domain (thanks to the fast Fourier transform). However, the algorithm differs from the fast LMS algorithm in that block size it uses may be smaller than the filter length. If both are equal, then MDF reduces to the FLMS algorithm. The advantages of MDF over the (N)LMS algorithm are: * Lower algorithmic complexity * Partial de-correlation of the input (which 'may' lead to faster convergence) Variable definitions Let N be the length of the processing blocks, K be the number of blocks and \mathbf denote the 2Nx2N Fourier transform matrix. The variables are defined as: : \underline(\ell) = \mathbf\left \mathbf_, e(\ell N),\dots,e(\ell N-N-1) \rightT : \underline_k(\ell) = \mathrm \left\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Similarities Between Wiener And LMS
The Least mean squares filter solution converges to the Wiener filter solution, assuming that the unknown system is LTI and the noise is stationary. Both filters can be used to identify the impulse response of an unknown system, knowing only the original input signal and the output of the unknown system. By relaxing the error criterion to reduce current sample error instead of minimizing the total error over all of n, the LMS algorithm can be derived from the Wiener filter. Derivation of the Wiener filter for system identification Given a known input signal s /math>, the output of an unknown LTI system x /math> can be expressed as: x = \sum_^ h_ks -k+ w /math> where h_k is an unknown filter tap coefficients and w /math> is noise. The model system \hat /math>, using a Wiener filter solution with an order N, can be expressed as: \hat = \sum_^\hat_ks -k/math> where \hat_k are the filter tap coefficients to be determined. The error between the model and the unknown system ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Least Squares
The method of least squares is a standard approach in regression analysis to approximate the solution of overdetermined systems (sets of equations in which there are more equations than unknowns) by minimizing the sum of the squares of the residuals (a residual being the difference between an observed value and the fitted value provided by a model) made in the results of each individual equation. The most important application is in data fitting. When the problem has substantial uncertainties in the independent variable (the ''x'' variable), then simple regression and least-squares methods have problems; in such cases, the methodology required for fitting errors-in-variables models may be considered instead of that for least squares. Least squares problems fall into two categories: linear or ordinary least squares and nonlinear least squares, depending on whether or not the residuals are linear in all unknowns. The linear least-squares problem occurs in statistical regressio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Recursive Least Squares
Recursive least squares (RLS) is an adaptive filter algorithm that recursively finds the coefficients that minimize a weighted linear least squares cost function relating to the input signals. This approach is in contrast to other algorithms such as the least mean squares (LMS) that aim to reduce the mean square error. In the derivation of the RLS, the input signals are considered deterministic, while for the LMS and similar algorithms they are considered stochastic. Compared to most of its competitors, the RLS exhibits extremely fast convergence. However, this benefit comes at the cost of high computational complexity. Motivation RLS was discovered by Gauss but lay unused or ignored until 1950 when Plackett rediscovered the original work of Gauss from 1821. In general, the RLS can be used to solve any problem that can be solved by adaptive filters. For example, suppose that a signal d(n) is transmitted over an echoey, noisy channel that causes it to be received as :x(n)=\sum_^q ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Learning Rate
In machine learning and statistics, the learning rate is a tuning parameter in an optimization algorithm that determines the step size at each iteration while moving toward a minimum of a loss function. Since it influences to what extent newly acquired information overrides old information, it metaphorically represents the speed at which a machine learning model "learns". In the adaptive control literature, the learning rate is commonly referred to as gain. In setting a learning rate, there is a trade-off between the rate of convergence and overshooting. While the descent direction is usually determined from the gradient of the loss function, the learning rate determines how big a step is taken in that direction. A too high learning rate will make the learning jump over minima but a too low learning rate will either take too long to converge or get stuck in an undesirable local minimum. In order to achieve faster convergence, prevent oscillations and getting stuck in undesirable ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trace (linear Algebra)
In linear algebra, the trace of a square matrix , denoted , is defined to be the sum of elements on the main diagonal (from the upper left to the lower right) of . The trace is only defined for a square matrix (). It can be proved that the trace of a matrix is the sum of its (complex) eigenvalues (counted with multiplicities). It can also be proved that for any two matrices and . This implies that similar matrices have the same trace. As a consequence one can define the trace of a linear operator mapping a finite-dimensional vector space into itself, since all matrices describing such an operator with respect to a basis are similar. The trace is related to the derivative of the determinant (see Jacobi's formula). Definition The trace of an square matrix is defined as \operatorname(\mathbf) = \sum_^n a_ = a_ + a_ + \dots + a_ where denotes the entry on the th row and th column of . The entries of can be real numbers or (more generally) complex numbers. The trace is not de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |