|
Lyndon–Hochschild–Serre Spectral Sequence
In mathematics, especially in the fields of group cohomology, homological algebra and number theory, the Lyndon spectral sequence or Hochschild–Serre spectral sequence is a spectral sequence relating the group cohomology of a normal subgroup ''N'' and the quotient group ''G''/''N'' to the cohomology of the total group ''G''. The spectral sequence is named after Roger Lyndon, Gerhard Hochschild, and Jean-Pierre Serre. Statement Let G be a group and N be a normal subgroup. The latter ensures that the quotient G/N is a group, as well. Finally, let A be a G-module. Then there is a spectral sequence of cohomological type :H^p(G/N,H^q(N,A)) \Longrightarrow H^(G,A) and there is a spectral sequence of homological type :H_p(G/N,H_q(N,A)) \Longrightarrow H_(G,A), where the arrow '\Longrightarrow' means convergence of spectral sequences. The same statement holds if G is a profinite group, N is a ''closed'' normal subgroup and H^* denotes the continuous cohomology. Examples Hom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
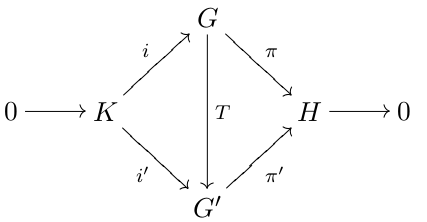
Group Extension
In mathematics, a group extension is a general means of describing a group in terms of a particular normal subgroup and quotient group. If Q and N are two groups, then G is an extension of Q by N if there is a short exact sequence :1\to N\;\overset\;G\;\overset\;Q \to 1. If G is an extension of Q by N, then G is a group, \iota(N) is a normal subgroup of G and the quotient group G/\iota(N) is isomorphic to the group Q. Group extensions arise in the context of the extension problem, where the groups Q and N are known and the properties of G are to be determined. Note that the phrasing "G is an extension of N by Q" is also used by some. Since any finite group G possesses a maximal normal subgroup N with simple factor group G/N, all finite groups may be constructed as a series of extensions with finite simple groups. This fact was a motivation for completing the classification of finite simple groups. An extension is called a central extension if the subgroup N lies in the c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transactions Of The American Mathematical Society
The ''Transactions of the American Mathematical Society'' is a monthly peer-reviewed scientific journal of mathematics published by the American Mathematical Society. It was established in 1900. As a requirement, all articles must be more than 15 printed pages. See also * ''Bulletin of the American Mathematical Society'' * '' Journal of the American Mathematical Society'' * '' Memoirs of the American Mathematical Society'' * '' Notices of the American Mathematical Society'' * '' Proceedings of the American Mathematical Society'' External links * ''Transactions of the American Mathematical Society''on JSTOR JSTOR (; short for ''Journal Storage'') is a digital library founded in 1995 in New York City. Originally containing digitized back issues of academic journals, it now encompasses books and other primary sources as well as current issues of j ... American Mathematical Society academic journals Mathematics journals Publications established in 1900 {{math-journa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Duke Mathematical Journal
''Duke Mathematical Journal'' is a peer-reviewed mathematics journal published by Duke University Press. It was established in 1935. The founding editors-in-chief were David Widder, Arthur Coble, and Joseph Miller Thomas. The first issue included a paper by Solomon Lefschetz. Leonard Carlitz served on the editorial board for 35 years, from 1938 to 1973. The current managing editor is Richard Hain (Duke University). Impact According to the journal homepage, the journal has a 2018 impact factor of 2.194, ranking it in the top ten mathematics journals in the world. References External links * Mathematics journals Mathematical Journal In academic publishing, a scientific journal is a periodical publication intended to further the progress of science, usually by reporting new research. Content Articles in scientific journals are mostly written by active scientists such as s ... Publications established in 1935 Multilingual journals English-language journals French-lan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cambridge University Press
Cambridge University Press is the university press of the University of Cambridge. Granted letters patent by Henry VIII of England, King Henry VIII in 1534, it is the oldest university press in the world. It is also the King's Printer. Cambridge University Press is a department of the University of Cambridge and is both an academic and educational publisher. It became part of Cambridge University Press & Assessment, following a merger with Cambridge Assessment in 2021. With a global sales presence, publishing hubs, and offices in more than 40 Country, countries, it publishes over 50,000 titles by authors from over 100 countries. Its publishing includes more than 380 academic journals, monographs, reference works, school and university textbooks, and English language teaching and learning publications. It also publishes Bibles, runs a bookshop in Cambridge, sells through Amazon, and has a conference venues business in Cambridge at the Pitt Building and the Sir Geoffrey Cass Spo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derived Functor
In mathematics, certain functors may be ''derived'' to obtain other functors closely related to the original ones. This operation, while fairly abstract, unifies a number of constructions throughout mathematics. Motivation It was noted in various quite different settings that a short exact sequence often gives rise to a "long exact sequence". The concept of derived functors explains and clarifies many of these observations. Suppose we are given a covariant left exact functor ''F'' : A → B between two abelian categories A and B. If 0 → ''A'' → ''B'' → ''C'' → 0 is a short exact sequence in A, then applying ''F'' yields the exact sequence 0 → ''F''(''A'') → ''F''(''B'') → ''F''(''C'') and one could ask how to continue this sequence to the right to form a long exact sequence. Strictly speaking, this question is ill-posed, since there are always numerous different ways to continue a given exact sequence to the right. But it turns out that (if A is "nice" enough) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Grothendieck Spectral Sequence
In mathematics, in the field of homological algebra, the Grothendieck spectral sequence, introduced by Alexander Grothendieck in his ''Tôhoku'' paper, is a spectral sequence that computes the derived functors of the composition of two functors G\circ F, from knowledge of the derived functors of F and G. Many spectral sequences in algebraic geometry are instances of the Grothendieck spectral sequence, for example the Leray spectral sequence. Statement If F \colon\mathcal\to\mathcal and G \colon \mathcal\to\mathcal are two additive and left exact functors between abelian categories such that both \mathcal and \mathcal have enough injectives and F takes injective objects to G- acyclic objects, then for each object A of \mathcal there is a spectral sequence: :E_2^ = (^p G \circ^q F)(A) \Longrightarrow ^ (G\circ F)(A), where ^p G denotes the ''p''-th right-derived functor of G, etc., and where the arrow '\Longrightarrow' means convergence of spectral sequences. Five term e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inflation-restriction Exact Sequence
In mathematics, the inflation-restriction exact sequence is an exact sequence occurring in group cohomology and is a special case of the five-term exact sequence arising from the study of spectral sequences. Specifically, let ''G'' be a group, ''N'' a normal subgroup, and ''A'' an abelian group which is equipped with an action of ''G'', i.e., a homomorphism In algebra, a homomorphism is a structure-preserving map between two algebraic structures of the same type (such as two groups, two rings, or two vector spaces). The word ''homomorphism'' comes from the Ancient Greek language: () meaning "same" ... from ''G'' to the automorphism group of ''A''. The quotient group ''G''/''N'' acts on ::''A''''N'' = . : Then the inflation-restriction exact sequence is: ::0 → ''H'' 1(''G''/''N'', ''A''''N'') → ''H'' 1(''G'', ''A'') → ''H'' 1(''N'', ''A'')''G''/''N'' → ''H'' 2(''G''/''N'', ''A''''N'') →''H'' 2(''G'', ''A'') : In this sequence, there are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Five-term Exact Sequence
In mathematics, five-term exact sequence or exact sequence of low-degree terms is a sequence of terms related to the first step of a spectral sequence. More precisely, let :E_2^ \Rightarrow H^n(A) be a first quadrant spectral sequence, meaning that E_2^ vanishes except when ''p'' and ''q'' are both non-negative. Then there is an exact sequence :0 → ''E''21,0 → ''H'' 1(''A'') → ''E''20,1 → ''E''22,0 → ''H'' 2(''A''). Here, the map E_2^ \to E_2^ is the differential of the E_2-term of the spectral sequence. Example *The inflation-restriction exact sequence ::0 → ''H'' 1(''G''/''N'', ''A''''N'') → ''H'' 1(''G'', ''A'') → ''H'' 1(''N'', ''A'')''G''/''N'' → ''H'' 2(''G''/''N'', ''A''''N'') →''H'' 2(''G'', ''A'') :in group cohomology arises as the five-term exact sequence associated to the Lyndon–Hochschild–Serre spectral sequence ::''H'' ''p''(''G''/''N'', ''H'' ''q''(''N'', ''A'')) ⇒ ''H'' ''p+q''(''G, ''A'') ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Manuscripta Mathematica
The Knights of Columbus Vatican Film Library in St. Louis, Missouri is the only collection, outside the Vatican itself, of microfilms of more than 37,000 works from the ''Biblioteca Apostolica Vaticana'', the Vatican Library in Europe. It is located in the Pius XII Memorial Library on the campus of Saint Louis University. History The Library was created by Lowrie J. Daly (1914–2000), with funding from the Knights of Columbus. The goal was to make Vatican and other documents more available to researchers in North America. Microfilming of Vatican manuscripts began in 1951, and according to the Library's website, was the largest microfilming project that had been undertaken up to that date. From 1951 to 1957, twelve million manuscript pages were recorded, from 30,000 different works. This represents approximately 75% of the manuscripts available in the targeted language groups. Other microfilm projects in the 1950s included Jesuit archival material from Rome, archives in both Nor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Annals Of Mathematics
The ''Annals of Mathematics'' is a mathematical journal published every two months by Princeton University and the Institute for Advanced Study. History The journal was established as ''The Analyst'' in 1874 and with Joel E. Hendricks as the founding editor-in-chief. It was "intended to afford a medium for the presentation and analysis of any and all questions of interest or importance in pure and applied Mathematics, embracing especially all new and interesting discoveries in theoretical and practical astronomy, mechanical philosophy, and engineering". It was published in Des Moines, Iowa, and was the earliest American mathematics journal to be published continuously for more than a year or two. This incarnation of the journal ceased publication after its tenth year, in 1883, giving as an explanation Hendricks' declining health, but Hendricks made arrangements to have it taken over by new management, and it was continued from March 1884 as the ''Annals of Mathematics''. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wreath Product
In group theory, the wreath product is a special combination of two groups based on the semidirect product. It is formed by the action of one group on many copies of another group, somewhat analogous to exponentiation. Wreath products are used in the classification of permutation groups and also provide a way of constructing interesting examples of groups. Given two groups A and H (sometimes known as the ''bottom'' and ''top''), there exist two variations of the wreath product: the unrestricted wreath product A \text H and the restricted wreath product A \text H. The general form, denoted by A \text_ H or A \text_ H respectively, requires that H acts on some set \Omega; when unspecified, usually \Omega = H (a regular wreath product), though a different \Omega is sometimes implied. The two variations coincide when A, H, and \Omega are all finite. Either variation is also denoted as A \wr H (with \wr for the LaTeX symbol) or ''A'' ≀ ''H'' (Unicode U+2240). The notion ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |