|
Low-rank Matrix Approximations
Low-rank matrix approximations are essential tools in the application of ''kernel methods to large-scale learning'' problems.Francis R. Bach and Michael I. Jordan (2005)"Predictive low-rank decomposition for kernel methods" ''ICML''. Kernel methods (for instance, support vector machines or Gaussian processes) project data points into a high-dimensional or infinite-dimensional feature space and find the optimal splitting hyperplane. In the kernel method the data is represented in a ''kernel matrix'' (or, Gram matrix). Many algorithms can solve machine learning problems using the ''kernel matrix''. The main problem of kernel method is its high computational cost associated with ''kernel matrices''. The cost is at least quadratic in the number of training data points, but most kernel methods include computation of matrix inversion or eigenvalue decomposition and the cost becomes cubic in the number of training data. Large training sets cause large storage and computational c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Support Vector Machine
In machine learning, support vector machines (SVMs, also support vector networks) are supervised learning models with associated learning algorithms that analyze data for classification and regression analysis. Developed at AT&T Bell Laboratories by Vladimir Vapnik with colleagues (Boser et al., 1992, Guyon et al., 1993, Cortes and Vapnik, 1995, Vapnik et al., 1997) SVMs are one of the most robust prediction methods, being based on statistical learning frameworks or VC theory proposed by Vapnik (1982, 1995) and Chervonenkis (1974). Given a set of training examples, each marked as belonging to one of two categories, an SVM training algorithm builds a model that assigns new examples to one category or the other, making it a non-probabilistic binary linear classifier (although methods such as Platt scaling exist to use SVM in a probabilistic classification setting). SVM maps training examples to points in space so as to maximise the width of the gap between the two categories. N ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Singular Value
In mathematics, in particular functional analysis, the singular values, or ''s''-numbers of a compact operator T: X \rightarrow Y acting between Hilbert spaces X and Y, are the square roots of the (necessarily non-negative) eigenvalues of the self-adjoint operator T^*T (where T^* denotes the adjoint of T). The singular values are non-negative real numbers, usually listed in decreasing order (''σ''1(''T''), ''σ''2(''T''), …). The largest singular value ''σ''1(''T'') is equal to the operator norm of ''T'' (see Min-max theorem). If ''T'' acts on Euclidean space \Reals ^n, there is a simple geometric interpretation for the singular values: Consider the image by T of the unit sphere; this is an ellipsoid, and the lengths of its semi-axes are the singular values of T (the figure provides an example in \Reals^2). The singular values are the absolute values of the eigenvalues of a normal matrix ''A'', because the spectral theorem can be applied to obtain unitary diagonaliza ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
L1 Distance
A taxicab geometry or a Manhattan geometry is a geometry whose usual distance function or metric of Euclidean geometry is replaced by a new metric in which the distance between two points is the sum of the absolute differences of their Cartesian coordinates. The taxicab metric is also known as rectilinear distance, ''L''1 distance, ''L''1 distance or \ell_1 norm (see ''Lp'' space), snake distance, city block distance, Manhattan distance or Manhattan length. The latter names refer to the rectilinear street layout on the island of Manhattan, where the shortest path a taxi travels between two points is the sum of the absolute values of distances that it travels on avenues and on streets. The geometry has been used in regression analysis since the 18th century, and is often referred to as LASSO. The geometric interpretation dates to non-Euclidean geometry of the 19th century and is due to Hermann Minkowski. In \mathbb^2 , the taxicab distance between two points (x_1, y_1) and (x_2, y_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a mathematical formalization of a quantity or object which depends on random events. It is a mapping or a function from possible outcomes (e.g., the possible upper sides of a flipped coin such as heads H and tails T) in a sample space (e.g., the set \) to a measurable space, often the real numbers (e.g., \ in which 1 corresponding to H and -1 corresponding to T). Informally, randomness typically represents some fundamental element of chance, such as in the roll of a dice; it may also represent uncertainty, such as measurement error. However, the interpretation of probability is philosophically complicated, and even in specific cases is not always straightforward. The purely mathematical analysis of random variables is independent of such interpretational difficulties, and can be based upon a rigorous axiomatic setup. In the formal mathematical language of measure theory, a rando ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Transform
A Fourier transform (FT) is a mathematical transform that decomposes functions into frequency components, which are represented by the output of the transform as a function of frequency. Most commonly functions of time or space are transformed, which will output a function depending on temporal frequency or spatial frequency respectively. That process is also called ''analysis''. An example application would be decomposing the waveform of a musical chord into terms of the intensity of its constituent pitches. The term ''Fourier transform'' refers to both the frequency domain representation and the mathematical operation that associates the frequency domain representation to a function of space or time. The Fourier transform of a function is a complex-valued function representing the complex sinusoids that comprise the original function. For each frequency, the magnitude ( absolute value) of the complex value represents the amplitude of a constituent complex sinusoid wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
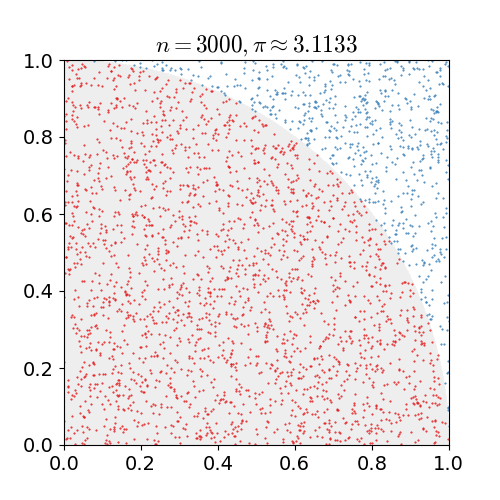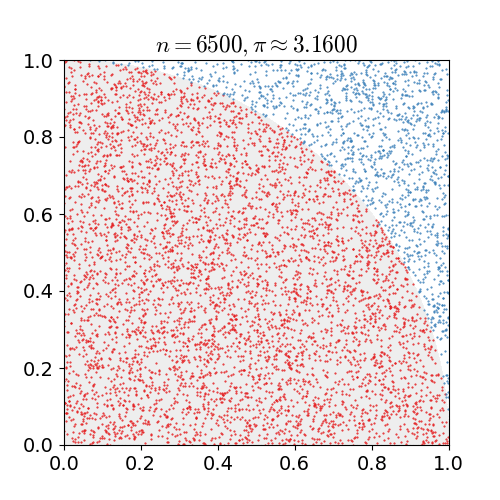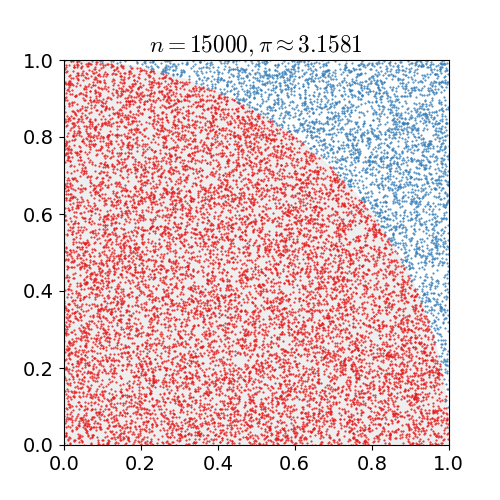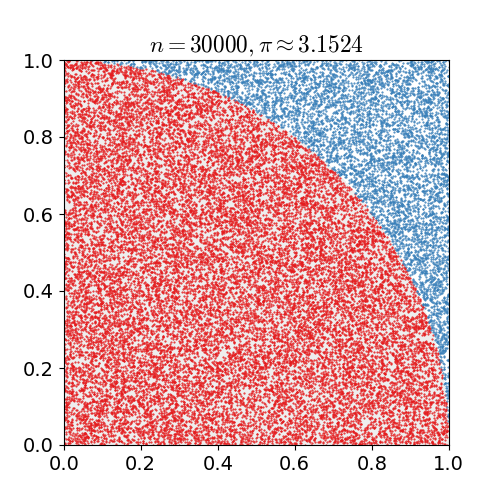
Monte Carlo Method
Monte Carlo methods, or Monte Carlo experiments, are a broad class of computational algorithms that rely on repeated random sampling to obtain numerical results. The underlying concept is to use randomness to solve problems that might be deterministic in principle. They are often used in physical and mathematical problems and are most useful when it is difficult or impossible to use other approaches. Monte Carlo methods are mainly used in three problem classes: optimization, numerical integration, and generating draws from a probability distribution. In physics-related problems, Monte Carlo methods are useful for simulating systems with many coupled degrees of freedom, such as fluids, disordered materials, strongly coupled solids, and cellular structures (see cellular Potts model, interacting particle systems, McKean–Vlasov processes, kinetic models of gases). Other examples include modeling phenomena with significant uncertainty in inputs such as the calculation of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radial Basis Function Kernel
In machine learning, the radial basis function kernel, or RBF kernel, is a popular kernel function used in various kernelized learning algorithms. In particular, it is commonly used in support vector machine classification. The RBF kernel on two samples \mathbf\in \mathbb^ and x', represented as feature vectors in some ''input space'', is defined asJean-Philippe Vert, Koji Tsuda, and Bernhard Schölkopf (2004)"A primer on kernel methods".''Kernel Methods in Computational Biology''. :K(\mathbf, \mathbf) = \exp\left(-\frac\right) \textstyle\, \mathbf - \mathbf\, ^2 may be recognized as the squared Euclidean distance between the two feature vectors. \sigma is a free parameter. An equivalent definition involves a parameter \textstyle\gamma = \tfrac: :K(\mathbf, \mathbf) = \exp(-\gamma\, \mathbf - \mathbf\, ^2) Since the value of the RBF kernel decreases with distance and ranges between zero (in the limit) and one (when ), it has a ready interpretation as a similarity measure. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Feature Map
Feature may refer to: Computing * Feature (CAD), could be a hole, pocket, or notch * Feature (computer vision), could be an edge, corner or blob * Feature (software design) is an intentional distinguishing characteristic of a software item (in performance, portability, or—especially—functionality) * Feature (machine learning), in statistics: individual measurable properties of the phenomena being observed Science and analysis * Feature data, in geographic information systems, comprise information about an entity with a geographic location * Features, in audio signal processing, an aim to capture specific aspects of audio signals in a numeric way * Feature (archaeology), any dug, built, or dumped evidence of human activity Media * Feature film, a film with a running time long enough to be considered the principal or sole film to fill a program ** Feature length, the standardized length of such films * Feature story, a piece of non-fiction writing about news * Radio doc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Woodbury Matrix Identity
In mathematics (specifically linear algebra), the Woodbury matrix identity, named after Max A. Woodbury, says that the inverse of a rank-''k'' correction of some matrix can be computed by doing a rank-''k'' correction to the inverse of the original matrix. Alternative names for this formula are the matrix inversion lemma, Sherman–Morrison–Woodbury formula or just Woodbury formula. However, the identity appeared in several papers before the Woodbury report. The Woodbury matrix identity is : \left(A + UCV \right)^ = A^ - A^U \left(C^ + VA^U \right)^ VA^, where ''A'', ''U'', ''C'' and ''V'' are conformable matrices: ''A'' is ''n''×''n'', ''C'' is ''k''×''k'', ''U'' is ''n''×''k'', and ''V'' is ''k''×''n''. This can be derived using blockwise matrix inversion. While the identity is primarily used on matrices, it holds in a general ring or in an Ab-category. Discussion To prove this result, we will start by proving a simpler one. Replacing ''A'' and ''C'' with the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regularized Least Squares
Regularized least squares (RLS) is a family of methods for solving the least squares, least-squares problem while using regularization (mathematics), regularization to further constrain the resulting solution. RLS is used for two main reasons. The first comes up when the number of variables in the linear system exceeds the number of observations. In such settings, the ordinary least squares, ordinary least-squares problem is ill-posed problem, ill-posed and is therefore impossible to fit because the associated optimization problem has infinitely many solutions. RLS allows the introduction of further constraints that uniquely determine the solution. The second reason for using RLS arises when the learned model suffers from poor Generalization error, generalization. RLS can be used in such cases to improve the generalizability of the model by constraining it at training time. This constraint can either force the solution to be "sparse" in some way or to reflect other prior knowledge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix Multiplication
In mathematics, particularly in linear algebra, matrix multiplication is a binary operation that produces a matrix from two matrices. For matrix multiplication, the number of columns in the first matrix must be equal to the number of rows in the second matrix. The resulting matrix, known as the matrix product, has the number of rows of the first and the number of columns of the second matrix. The product of matrices and is denoted as . Matrix multiplication was first described by the French mathematician Jacques Philippe Marie Binet in 1812, to represent the composition of linear maps that are represented by matrices. Matrix multiplication is thus a basic tool of linear algebra, and as such has numerous applications in many areas of mathematics, as well as in applied mathematics, statistics, physics, economics, and engineering. Computing matrix products is a central operation in all computational applications of linear algebra. Notation This article will use the following n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthogonal Matrix
In linear algebra, an orthogonal matrix, or orthonormal matrix, is a real square matrix whose columns and rows are orthonormal vectors. One way to express this is Q^\mathrm Q = Q Q^\mathrm = I, where is the transpose of and is the identity matrix. This leads to the equivalent characterization: a matrix is orthogonal if its transpose is equal to its inverse: Q^\mathrm=Q^, where is the inverse of . An orthogonal matrix is necessarily invertible (with inverse ), unitary (), where is the Hermitian adjoint (conjugate transpose) of , and therefore normal () over the real numbers. The determinant of any orthogonal matrix is either +1 or −1. As a linear transformation, an orthogonal matrix preserves the inner product of vectors, and therefore acts as an isometry of Euclidean space, such as a rotation, reflection or rotoreflection. In other words, it is a unitary transformation. The set of orthogonal matrices, under multiplication, forms the group , known as the o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |