|
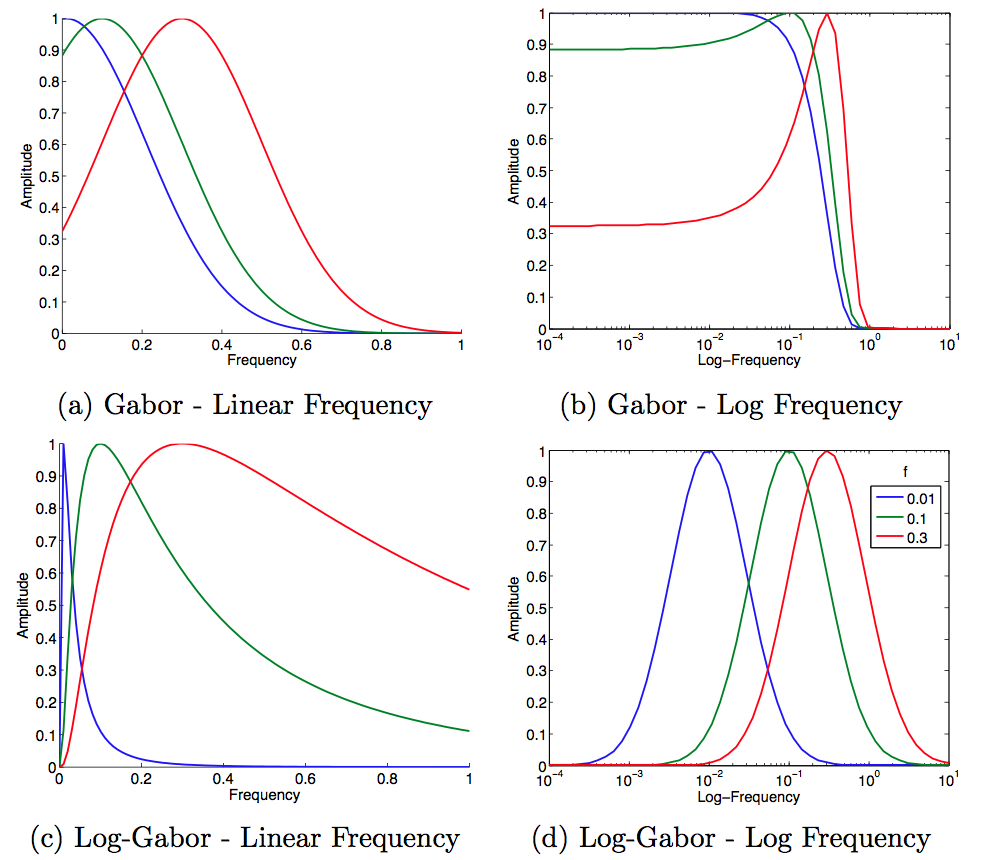
Log Gabor Filter
In signal processing it is useful to simultaneously analyze the space and frequency characteristics of a signal. While the Fourier transform gives the frequency information of the signal, it is not localized. This means that we cannot determine which part of a (perhaps long) signal produced a particular frequency. It is possible to use a short time Fourier transform for this purpose, however the short time Fourier transform limits the basis functions to be sinusoidal. To provide a more flexible space-frequency signal decomposition several filters (including wavelets) have been proposed. The Log-GaborD. J. FieldRelations between the statistics of natural images and the response properties of cortical cells J. Opt. Soc. Am. A, 1987, pp. 2379–2394. filter is one such filter that is an improvement upon the original Gabor filter.D. Gabor. Theory of communication. J. Inst. Electr. Eng. 93, 1946. The advantage of this filter over the many alternatives is that it better fits the statisti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Transform
A Fourier transform (FT) is a mathematical transform that decomposes functions into frequency components, which are represented by the output of the transform as a function of frequency. Most commonly functions of time or space are transformed, which will output a function depending on temporal frequency or spatial frequency respectively. That process is also called ''analysis''. An example application would be decomposing the waveform of a musical chord into terms of the intensity of its constituent pitches. The term ''Fourier transform'' refers to both the frequency domain representation and the mathematical operation that associates the frequency domain representation to a function of space or time. The Fourier transform of a function is a complex-valued function representing the complex sinusoids that comprise the original function. For each frequency, the magnitude ( absolute value) of the complex value represents the amplitude of a constituent complex sinusoid wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ridge Detection
In image processing, ridge detection is the attempt, via software, to locate ridges in an image, defined as curves whose points are local maxima of the function, akin to geographical ridges. For a function of ''N'' variables, its ridges are a set of curves whose points are local maxima in ''N'' − 1 dimensions. In this respect, the notion of ridge points extends the concept of a local maximum. Correspondingly, the notion of valleys for a function can be defined by replacing the condition of a local maximum with the condition of a local minimum. The union of ridge sets and valley sets, together with a related set of points called the connector set, form a connected set of curves that partition, intersect, or meet at the critical points of the function. This union of sets together is called the function's relative critical set.Miller, J. ''Relative Critical Sets in \mathbb^n and Applications to Image Analysis.'' Ph.D. Dissertation. University of North Carolina. 1998. Ridge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Image Noise Reduction
Noise reduction is the process of removing noise from a signal. Noise reduction techniques exist for audio and images. Noise reduction algorithms may distort the signal to some degree. Noise rejection is the ability of a circuit to isolate an undesired signal component from the desired signal component, as with common-mode rejection ratio. All signal processing devices, both analog and digital, have traits that make them susceptible to noise. Noise can be random with an even frequency distribution (white noise), or frequency-dependent noise introduced by a device's mechanism or signal processing algorithms. In electronic systems, a major type of noise is ''hiss'' created by random electron motion due to thermal agitation. These agitated electrons rapidly add and subtract from the output signal and thus create detectable noise. In the case of photographic film and magnetic tape, noise (both visible and audible) is introduced due to the grain structure of the medium. In photogra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Image Derivative
Image derivatives can be computed by using small convolution filters of size 2 × 2 or 3 × 3, such as the Laplacian, Sobel, Roberts and Prewitt operators. However, a larger mask will generally give a better approximation of the derivative and examples of such filters are Gaussian derivatives and Gabor filters. Sometimes high frequency noise needs to be removed and this can be incorporated in the filter so that the Gaussian kernel will act as a band pass filter. The use of Gabor filters in image processing has been motivated by some of its similarities to the perception in the human visual system. The pixel value is computed as a convolution : p'_u=\mathbf \ast G where \mathbf is the derivative kernel and G is the pixel values in a region of the image and \ast is the operator that performs the convolution. Sobel derivatives The derivative kernels, known as the Sobel operator are defined as follows, for the u and v directions respectively: : p'_u = \begin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Feature Detection (computer Vision)
In computer vision and image processing, a feature is a piece of information about the content of an image; typically about whether a certain region of the image has certain properties. Features may be specific structures in the image such as points, edges or objects. Features may also be the result of a general neighborhood operation or feature detection applied to the image. Other examples of features are related to motion in image sequences, or to shapes defined in terms of curves or boundaries between different image regions. More broadly a ''feature'' is any piece of information which is relevant for solving the computational task related to a certain application. This is the same sense as feature in machine learning and pattern recognition generally, though image processing has a very sophisticated collection of features. The feature concept is very general and the choice of features in a particular computer vision system may be highly dependent on the specific problem at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
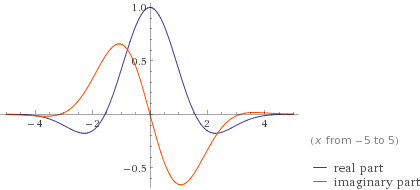
Gabor Atom
In applied mathematics, Gabor atoms, or Gabor functions, are functions used in the analysis proposed by Dennis Gabor in 1946 in which a family of functions is built from translations and modulations of a generating function. Overview In 1946, Dennis Gabor suggested the idea of using a granular system to produce sound. In his work, Gabor discussed the problems with Fourier analysis. Although he found the mathematics to be correct, it did not reflect the behaviour of sound in the world, because sounds, such as the sound of a siren, have variable frequencies over time. Another problem was the underlying supposition, as we use sine waves analysis, that the signal under concern has infinite duration even though sounds in real life have limited duration – see time–frequency analysis. Gabor applied ideas from quantum physics to sound, allowing an analogy between sound and quanta. He proposed a mathematical method to reduce Fourier analysis into cells. His research aimed at the info ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gabor Wavelet
Gabor wavelets are wavelets invented by Dennis Gabor using complex functions constructed to serve as a basis for Fourier transforms in information theory applications. They are very similar to Morlet wavelets. They are also closely related to Gabor filters. The important property of the wavelet is that it minimizes the product of its standard deviations in the time and frequency domain. Put another way, the uncertainty in information carried by this wavelet is minimized. However they have the downside of being non-orthogonal, so efficient decomposition into the basis is difficult. Since their inception, various applications have appeared, from image processing to analyzing neurons in the human visual system. Minimal uncertainty property The motivation for Gabor wavelets comes from finding some function f(x) which minimizes its standard deviation in the time and frequency domains. More formally, the variance in the position domain is: : (\Delta x)^2 = \frac where f^(x) is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
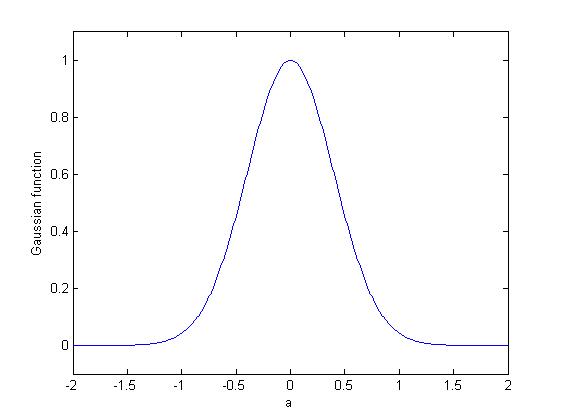
Gabor Transform
The Gabor transform, named after Dennis Gabor, is a special case of the short-time Fourier transform. It is used to determine the sinusoidal frequency and phase content of local sections of a signal as it changes over time. The function to be transformed is first multiplied by a Gaussian function, which can be regarded as a window function, and the resulting function is then transformed with a Fourier transform to derive the time-frequency analysis.E. Sejdić, I. Djurović, J. Jiang, “Time-frequency feature representation using energy concentration: An overview of recent advances,” ''Digital Signal Processing'', vol. 19, no. 1, pp. 153-183, January 2009. The window function means that the signal near the time being analyzed will have higher weight. The Gabor transform of a signal ''x''(''t'') is defined by this formula: : G_x(\tau,\omega) = \int_^\infty x(t)e^e^\,dt The Gaussian function has infinite range and it is impractical for implementation. However, a level of signi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Filter Bank
In signal processing, a filter bank (or filterbank) is an array of bandpass filters that separates the input signal into multiple components, each one carrying a single frequency sub-band of the original signal. One application of a filter bank is a graphic equalizer, which can attenuate the components differently and recombine them into a modified version of the original signal. The process of decomposition performed by the filter bank is called ''analysis'' (meaning analysis of the signal in terms of its components in each sub-band); the output of analysis is referred to as a subband signal with as many subbands as there are filters in the filter bank. The reconstruction process is called ''synthesis'', meaning reconstitution of a complete signal resulting from the filtering process. In digital signal processing, the term ''filter bank'' is also commonly applied to a bank of receivers. The difference is that receivers also down-convert the subbands to a low center frequency th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time-domain
Time domain refers to the analysis of mathematical functions, physical signals or time series of economic or environmental data, with respect to time. In the time domain, the signal or function's value is known for all real numbers, for the case of continuous time, or at various separate instants in the case of discrete time. An oscilloscope is a tool commonly used to visualize real-world signals in the time domain. A time-domain graph shows how a signal changes with time, whereas a frequency-domain graph shows how much of the signal lies within each given frequency band over a range of frequencies. Though most precisely referring to time in physics, the term ''time domain'' may occasionally informally refer to position in space when dealing with spatial frequencies, as a substitute for the more precise term ''spatial domain''. Origin of term The use of the contrasting terms ''time domain'' and ''frequency domain'' developed in U.S. communication engineering in the late 1940 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |




.gif)