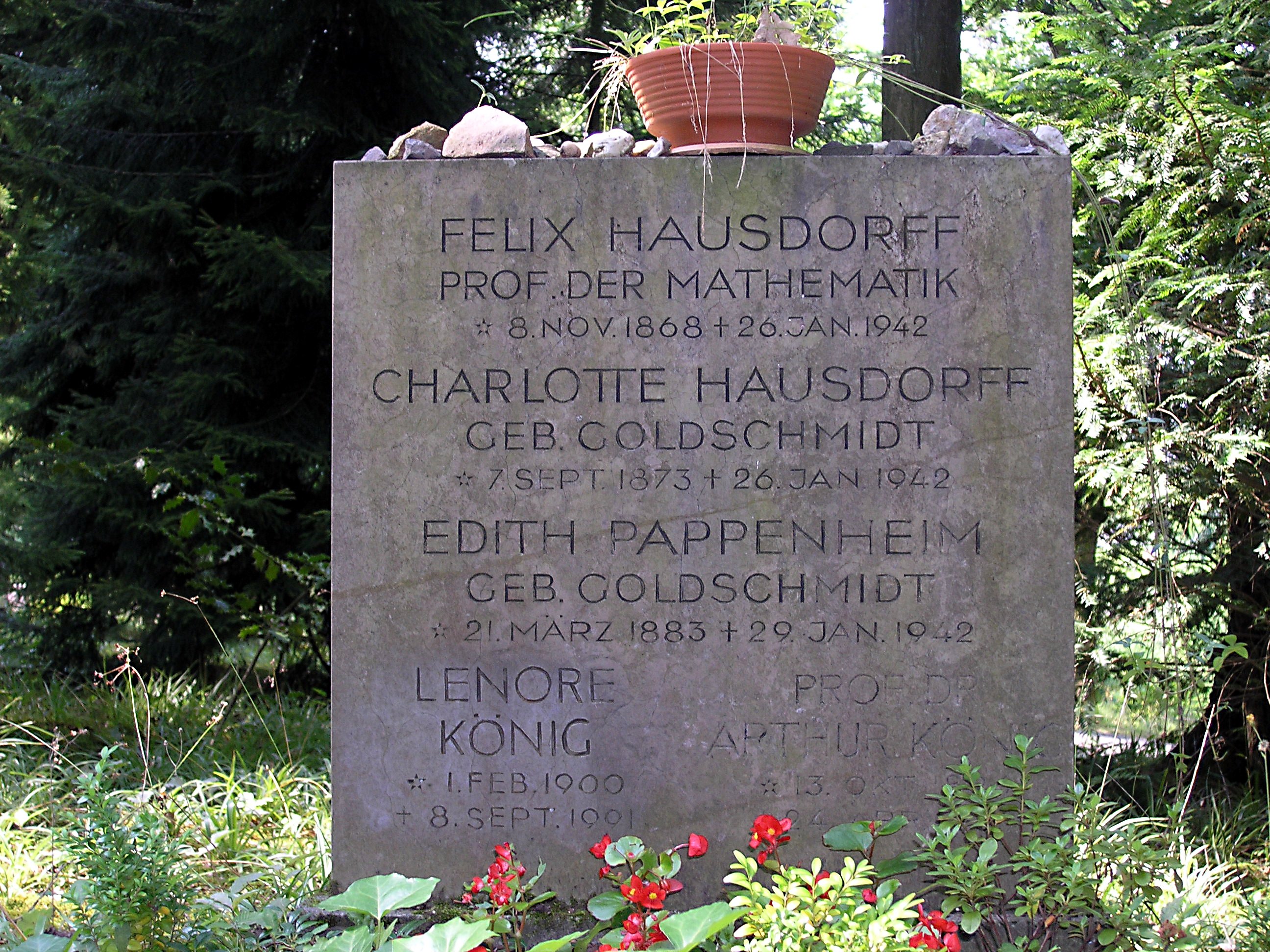|
Locally Convex Space
In functional analysis and related areas of mathematics, locally convex topological vector spaces (LCTVS) or locally convex spaces are examples of topological vector spaces (TVS) that generalize normed spaces. They can be defined as topological vector spaces whose topology is generated by translations of balanced, absorbent, convex sets. Alternatively they can be defined as a vector space with a family of seminorms, and a topology can be defined in terms of that family. Although in general such spaces are not necessarily normable, the existence of a convex local base for the zero vector is strong enough for the Hahn–Banach theorem to hold, yielding a sufficiently rich theory of continuous linear functionals. Fréchet spaces are locally convex topological vector spaces that are completely metrizable (with a choice of complete metric). They are generalizations of Banach spaces, which are complete vector spaces with respect to a metric generated by a norm. History Metrizabl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Functional Analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure (for example, Inner product space#Definition, inner product, Norm (mathematics)#Definition, norm, or Topological space#Definitions, topology) and the linear transformation, linear functions defined on these spaces and suitably respecting these structures. The historical roots of functional analysis lie in the study of function space, spaces of functions and the formulation of properties of transformations of functions such as the Fourier transform as transformations defining, for example, continuous function, continuous or unitary operator, unitary operators between function spaces. This point of view turned out to be particularly useful for the study of differential equations, differential and integral equations. The usage of the word ''functional (mathematics), functional'' as a noun goes back to the calculus of v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fréchet Space
In functional analysis and related areas of mathematics, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces ( normed vector spaces that are complete with respect to the metric induced by the norm). All Banach and Hilbert spaces are Fréchet spaces. Spaces of infinitely differentiable functions are typical examples of Fréchet spaces, many of which are typically Banach spaces. A Fréchet space X is defined to be a locally convex metrizable topological vector space (TVS) that is complete as a TVS, meaning that every Cauchy sequence in X converges to some point in X (see footnote for more details).Here "Cauchy" means Cauchy with respect to the canonical uniformity that every TVS possess. That is, a sequence x_ = \left(x_m\right)_^ in a TVS X is Cauchy if and only if for all neighborhoods U of the origin in X, x_m - x_n \in U whenever m and n are sufficiently large. Note that this definiti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Banach–Alaoglu Theorem
In functional analysis and related branches of mathematics, the Banach–Alaoglu theorem (also known as Alaoglu's theorem) states that the closed unit ball of the dual space of a normed vector space is compact in the weak* topology. A common proof identifies the unit ball with the weak-* topology as a closed subset of a product of compact sets with the product topology. As a consequence of Tychonoff's theorem, this product, and hence the unit ball within, is compact. This theorem has applications in physics when one describes the set of states of an algebra of observables, namely that any state can be written as a convex linear combination of so-called pure states. History According to Lawrence Narici and Edward Beckenstein, the Alaoglu theorem is a “very important result—maybe most important fact about the weak-* topology—hatechos throughout functional analysis.” In 1912, Helly proved that the unit ball of the continuous dual space of C( , b is countably weak-* co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tychonoff's Theorem
In mathematics, Tychonoff's theorem states that the product of any collection of compact topological spaces is compact with respect to the product topology. The theorem is named after Andrey Nikolayevich Tikhonov (whose surname sometimes is transcribed ''Tychonoff''), who proved it first in 1930 for powers of the closed unit interval and in 1935 stated the full theorem along with the remark that its proof was the same as for the special case. The earliest known published proof is contained in a 1935 article by Tychonoff, . Tychonoff's theorem is often considered as perhaps the single most important result in general topology (along with Urysohn's lemma). The theorem is also valid for topological spaces based on fuzzy sets. Topological definitions The theorem depends crucially upon the precise definitions of compactness and of the product topology; in fact, Tychonoff's 1935 paper defines the product topology for the first time. Conversely, part of its importance is to gi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Product Topology
In topology and related areas of mathematics, a product space is the Cartesian product of a family of topological spaces equipped with a natural topology called the product topology. This topology differs from another, perhaps more natural-seeming, topology called the box topology, which can also be given to a product space and which Comparison of topologies, agrees with the product topology when the product is over only finitely many spaces. However, the product topology is "correct" in that it makes the product space a Product (category theory), categorical product of its factors, whereas the box topology is too Comparison of topologies, fine; in that sense the product topology is the natural topology on the Cartesian product. Definition Throughout, I will be some non-empty index set and for every index i \in I, let X_i be a topological space. Denote the Cartesian product of the sets X_i by X := \prod X_ := \prod_ X_i and for every index i \in I, denote the i-th by \begin p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Net (mathematics)
In mathematics, more specifically in general topology and related branches, a net or Moore–Smith sequence is a function whose domain is a directed set. The codomain of this function is usually some topological space. Nets directly generalize the concept of a sequence in a metric space. Nets are primarily used in the fields of analysis and topology, where they are used to characterize many important topological properties that (in general), sequences are unable to characterize (this shortcoming of sequences motivated the study of sequential spaces and Fréchet–Urysohn spaces). Nets are in one-to-one correspondence with filters. History The concept of a net was first introduced by E. H. Moore and Herman L. Smith in 1922. The term "net" was coined by John L. Kelley. The related concept of a filter was developed in 1937 by Henri Cartan. Definitions A directed set is a non-empty set A together with a preorder, typically automatically assumed to be denoted by \,\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Strong Operator Topology
In functional analysis, a branch of mathematics, the strong operator topology, often abbreviated SOT, is the locally convex topology on the set of bounded operators on a Hilbert space ''H'' induced by the seminorms of the form T\mapsto\, Tx\, , as ''x'' varies in ''H''. Equivalently, it is the coarsest topology such that, for each fixed ''x'' in ''H'', the evaluation map T\mapsto Tx (taking values in ''H'') is continuous in T. The equivalence of these two definitions can be seen by observing that a subbase for both topologies is given by the sets U(T_0,x,\epsilon) = \ (where ''T0'' is any bounded operator on ''H'', ''x'' is any vector and ε is any positive real number). In concrete terms, this means that T_i\to T in the strong operator topology if and only if \, T_ix-Tx\, \to 0 for each ''x'' in ''H''. The SOT is stronger than the weak operator topology and weaker than the norm topology. The SOT lacks some of the nicer properties that the weak operator topology has, but bein ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weak Topology
In mathematics, weak topology is an alternative term for certain initial topologies, often on topological vector spaces or spaces of linear operators, for instance on a Hilbert space. The term is most commonly used for the initial topology of a topological vector space (such as a normed vector space) with respect to its continuous dual. The remainder of this article will deal with this case, which is one of the concepts of functional analysis. One may call subsets of a topological vector space weakly closed (respectively, weakly compact, etc.) if they are closed (respectively, compact, etc.) with respect to the weak topology. Likewise, functions are sometimes called weakly continuous (respectively, weakly differentiable, weakly analytic, etc.) if they are continuous (respectively, differentiable, analytic, etc.) with respect to the weak topology. History Starting in the early 1900s, David Hilbert and Marcel Riesz made extensive use of weak convergence. The early pioneers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
John Von Neumann
John von Neumann ( ; ; December 28, 1903 – February 8, 1957) was a Hungarian and American mathematician, physicist, computer scientist and engineer. Von Neumann had perhaps the widest coverage of any mathematician of his time, integrating Basic research, pure and Applied science#Applied research, applied sciences and making major contributions to many fields, including mathematics, physics, economics, computing, and statistics. He was a pioneer in building the mathematical framework of quantum physics, in the development of functional analysis, and in game theory, introducing or codifying concepts including Cellular automaton, cellular automata, the Von Neumann universal constructor, universal constructor and the Computer, digital computer. His analysis of the structure of self-replication preceded the discovery of the structure of DNA. During World War II, von Neumann worked on the Manhattan Project. He developed the mathematical models behind the explosive lense ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Felix Hausdorff
Felix Hausdorff ( , ; November 8, 1868 – January 26, 1942) was a German mathematician, pseudonym Paul Mongré (''à mogré' (Fr.) = "according to my taste"), who is considered to be one of the founders of modern topology and who contributed significantly to set theory, descriptive set theory, measure theory, and functional analysis. Hausdorff was Jewish, and life became difficult for him and his family after the '' Kristallnacht'' of 1938. The next year he initiated efforts to emigrate to the United States, but was unable to make arrangements to receive a research fellowship. On 26 January 1942, Hausdorff, along with his wife and his sister-in-law, died by suicide by taking an overdose of veronal, rather than comply with German orders to move to the Endenich camp, and there suffer the likely implications, about which he held no illusions. Life Childhood and youth Hausdorff's father, the Jewish merchant Louis Hausdorff (1843–1896), moved with his young family to Leipzig in t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Metric Space
In mathematics, a metric space is a Set (mathematics), set together with a notion of ''distance'' between its Element (mathematics), elements, usually called point (geometry), points. The distance is measured by a function (mathematics), function called a metric or distance function. Metric spaces are a general setting for studying many of the concepts of mathematical analysis and geometry. The most familiar example of a metric space is 3-dimensional Euclidean space with its usual notion of distance. Other well-known examples are a sphere equipped with the angular distance and the hyperbolic plane. A metric may correspond to a Conceptual metaphor , metaphorical, rather than physical, notion of distance: for example, the set of 100-character Unicode strings can be equipped with the Hamming distance, which measures the number of characters that need to be changed to get from one string to another. Since they are very general, metric spaces are a tool used in many different bra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maurice René Fréchet
Maurice may refer to: *Maurice (name), a given name and surname, including a list of people with the name Places * or Mauritius, an island country in the Indian Ocean *Maurice, Iowa, a city * Maurice, Louisiana, a village * Maurice River, a tributary of the Delaware River in New Jersey Other uses * ''Maurice'' (2015 film), a Canadian short drama film * Maurice (horse), a Thoroughbred racehorse * ''Maurice'' (novel), a 1913 novel by E. M. Forster, published in 1971 ** ''Maurice'' (1987 film), a British film based on the novel * ''Maurice'' (Shelley), a children's story by Mary Shelley *Maurice, a character from the Madagascar ''franchise'' *Maurices, an American retail clothing chain *Maurice or Maryse, a type of cooking spatula See also *Church of Saint Maurice (other) * *Maurice Debate, a 1918 debate in the British House of Commons *Maurice Lacroix, Swiss manufacturer of mechanical timepieces, clocks, and watches *Mauricie, Quebec, Canada *Moritz (other) * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |