|
Local Volatility
A local volatility model, in mathematical finance and financial engineering, is an option pricing model that treats Volatility (finance), volatility as a function of both the current asset level S_t and of time t . As such, it is a generalisation of the Black–Scholes model, where the volatility is a constant (i.e. a trivial function of S_t and t ). Local volatility models are often compared with stochastic volatility, stochastic volatility models, where the instantaneous volatility is not just a function of the asset level S_t but depends also on a new "global" randomness coming from an additional random component. Formulation In mathematical finance, the asset ''S''''t'' that Underlying, underlies a financial derivative is typically assumed to follow a stochastic differential equation of the form : dS_t = (r_t-d_t) S_t\,dt + \sigma_t S_t\,dW_t , under the risk neutral measure, where r_t is the instantaneous risk-free interest rate, risk free rate, giving an average ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mathematical Finance
Mathematical finance, also known as quantitative finance and financial mathematics, is a field of applied mathematics, concerned with mathematical modeling in the financial field. In general, there exist two separate branches of finance that require advanced quantitative techniques: derivatives pricing on the one hand, and risk and portfolio management on the other. Mathematical finance overlaps heavily with the fields of computational finance and financial engineering. The latter focuses on applications and modeling, often with the help of stochastic asset models, while the former focuses, in addition to analysis, on building tools of implementation for the models. Also related is quantitative investing, which relies on statistical and numerical models (and lately machine learning) as opposed to traditional fundamental analysis when managing portfolios. French mathematician Louis Bachelier's doctoral thesis, defended in 1900, is considered the first scholarly work on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Implied Binomial Tree
In quantitative finance, a lattice model is a numerical approach to the valuation of derivatives in situations requiring a discrete time model. For dividend paying equity options, a typical application would correspond to the pricing of an American-style option, where a decision to exercise is allowed at the closing of any calendar day up to the maturity. A continuous model, on the other hand, such as the standard Black–Scholes one, would only allow for the valuation of European options, where exercise is limited to the option's maturity date. For interest rate derivatives lattices are additionally useful in that they address many of the issues encountered with continuous models, such as pull to par. The method is also used for valuing certain exotic options, because of path dependence in the payoff. Traditional Monte Carlo methods for option pricing fail to account for optimal decisions to terminate the derivative by early exercise, but some methods now exist for solvi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Constant Elasticity Of Variance Model
In mathematical finance, the CEV or constant elasticity of variance model is a stochastic volatility model, although technically it would be classed more precisely as a local volatility model, that attempts to capture stochastic volatility and the leverage effect. The model is widely used by practitioners in the financial industry, especially for modelling equities and commodities. It was developed by John Carrington Cox, John Cox in 1975. Dynamic The CEV model is a stochastic process which evolves according to the following stochastic differential equation: :\mathrmS_t = \mu S_t \mathrmt + \sigma S_t ^ \mathrmW_t in which ''S'' is the spot price, ''t'' is time, and ''μ'' is a parameter characterising the drift, ''σ'' and ''γ'' are volatility parameters, and ''W'' is a Brownian motion. It is a special case of a general local volatility model, written as :\mathrmS_t = \mu S_t \mathrmt + v(t,S_t) S_t \mathrmW_t where the price return volatility is :v(t, S_t)=\sigma S_t^ The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Stochastic Volatility
In statistics, stochastic volatility models are those in which the variance of a stochastic process is itself randomly distributed. They are used in the field of mathematical finance to evaluate derivative securities, such as options. The name derives from the models' treatment of the underlying security's volatility as a random process, governed by state variables such as the price level of the underlying security, the tendency of volatility to revert to some long-run mean value, and the variance of the volatility process itself, among others. Stochastic volatility models are one approach to resolve a shortcoming of the Black–Scholes model. In particular, models based on Black-Scholes assume that the underlying volatility is constant over the life of the derivative, and unaffected by the changes in the price level of the underlying security. However, these models cannot explain long-observed features of the implied volatility surface such as volatility smile and skew, w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Constant Elasticity Of Variance Model
In mathematical finance, the CEV or constant elasticity of variance model is a stochastic volatility model, although technically it would be classed more precisely as a local volatility model, that attempts to capture stochastic volatility and the leverage effect. The model is widely used by practitioners in the financial industry, especially for modelling equities and commodities. It was developed by John Carrington Cox, John Cox in 1975. Dynamic The CEV model is a stochastic process which evolves according to the following stochastic differential equation: :\mathrmS_t = \mu S_t \mathrmt + \sigma S_t ^ \mathrmW_t in which ''S'' is the spot price, ''t'' is time, and ''μ'' is a parameter characterising the drift, ''σ'' and ''γ'' are volatility parameters, and ''W'' is a Brownian motion. It is a special case of a general local volatility model, written as :\mathrmS_t = \mu S_t \mathrmt + v(t,S_t) S_t \mathrmW_t where the price return volatility is :v(t, S_t)=\sigma S_t^ The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Lognormal Distribution
In probability theory, a log-normal (or lognormal) distribution is a continuous probability distribution of a random variable whose logarithm is normal distribution, normally distributed. Thus, if the random variable is log-normally distributed, then has a normal distribution. Equivalently, if has a normal distribution, then the exponential function of , , has a log-normal distribution. A random variable which is log-normally distributed takes only positive real values. It is a convenient and useful model for measurements in exact and engineering sciences, as well as medicine, economics and other topics (e.g., energies, concentrations, lengths, prices of financial instruments, and other metrics). The distribution is occasionally referred to as the Galton distribution or Galton's distribution, after Francis Galton. The log-normal distribution has also been associated with other names, such as Donald MacAlister#log-normal, McAlister, Gibrat's law, Gibrat and Cobb–Douglas. A l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Geometric Brownian Motion
A geometric Brownian motion (GBM) (also known as exponential Brownian motion) is a continuous-time stochastic process in which the logarithm of the randomly varying quantity follows a Brownian motion (also called a Wiener process) with drift. It is an important example of stochastic processes satisfying a stochastic differential equation (SDE); in particular, it is used in mathematical finance to model stock prices in the Black–Scholes model. Technical definition: the SDE A stochastic process ''S''''t'' is said to follow a GBM if it satisfies the following stochastic differential equation (SDE): : dS_t = \mu S_t\,dt + \sigma S_t\,dW_t where W_t is a Wiener process or Brownian motion, and \mu ('the percentage drift') and \sigma ('the percentage volatility') are constants. The former parameter is used to model deterministic trends, while the latter parameter models unpredictable events occurring during the motion. Solving the SDE For an arbitrary initial value ''S' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mark Rubinstein
Mark Edward Rubinstein (June 8, 1944 – May 9, 2019) was a leading financial economics, financial economist and financial engineering, financial engineer. He was Paul Stephens Professor of Applied Investment Analysis at the Haas School of Business of the University of California, Berkeley. He held various other professional offices, directing the American Finance Association, amongst others, especially portfolio insurance and the binomial options pricing model (also known as the John Carrington Cox, Cox-Stephen Ross (economist), Ross-Rubinstein model), as well as his work on discrete time stochastic calculus more generally. His book ''Option Markets'', was "the first work that popularized probabilistic and scientific methods in options, helping inaugurate the derivatives revolution." Along with fellow Berkeley finance professor Hayne E. Leland and adjunct professor John O'Brien, Rubinstein developed the portfolio insurance financial product in 1976. (This strategy later became ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Louis Bachelier
Louis Jean-Baptiste Alphonse Bachelier (; 11 March 1870 – 28 April 1946) was a French mathematician at the turn of the 20th century. He is credited with being the first person to model the stochastic process now called Brownian motion, as part of his doctoral thesis ''The Theory of Speculation'' (''Théorie de la spéculation'', defended in 1900). Bachelier's doctoral thesis, which introduced the first mathematical model of Brownian motion and its use for valuing stock options, was the first paper to use advanced mathematics in the study of finance. His Bachelier model has been influential in the development of other widely used models, including the Black-Scholes model. Bachelier is considered as the forefather of mathematical finance and a pioneer in the study of stochastic processes. Early years Bachelier was born in Le Havre, in Seine-Maritime. His father was a wine merchant and amateur scientist, and the vice-consul of Venezuela at Le Havre. His mother was the da ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Bachelier Model
The Bachelier model is a model of an asset price under Brownian motion presented by Louis Bachelier on his PhD thesis ''The Theory of Speculation'' (''Théorie de la spéculation'', published 1900). It is also called "Normal Model" equivalently (as opposed to "Log-Normal Model" or "Black-Scholes Model"). One early criticism of the Bachelier model is that the probability distribution which he chose to use to describe stock prices allowed for negative prices. (His doctoral dissertation was graded down because of that feature.) The (much) later Black-Scholes-(Merton) Model addresses that issue by positing stock prices as following a log-normal distribution which does not allow negative values. This in turn, implies that returns follow a normal distribution. On April 8, 2020, the CME Group posted the note ''CME Clearing Plan to Address the Potential of a Negative Underlying in Certain Energy Options Contracts'', saying that after a threshold on price, it would change its standard e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Martingale Pricing
Martingale pricing is a pricing approach based on the notions of martingale and risk neutrality. The martingale pricing approach is a cornerstone of modern quantitative finance and can be applied to a variety of derivatives contracts, e.g. options, futures, interest rate derivatives, credit derivatives, etc. In contrast to the PDE approach to pricing, martingale pricing formulae are in the form of expectations which can be efficiently solved numerically using a Monte Carlo approach. As such, martingale pricing is preferred when valuing high-dimensional contracts such as a basket of options. On the other hand, valuing American-style contracts is troublesome and requires discretizing the problem (making it like a Bermudan option) and only in 2001 F. A. Longstaff and E. S. Schwartz developed a practical Monte Carlo method for pricing American options. Measure theory representation Suppose the state of the market can be represented by the filtered probability space,(\Omega,(\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
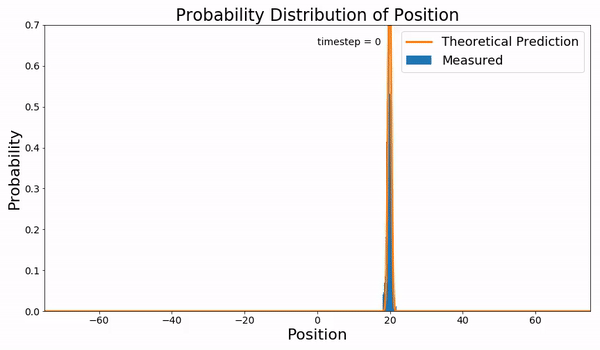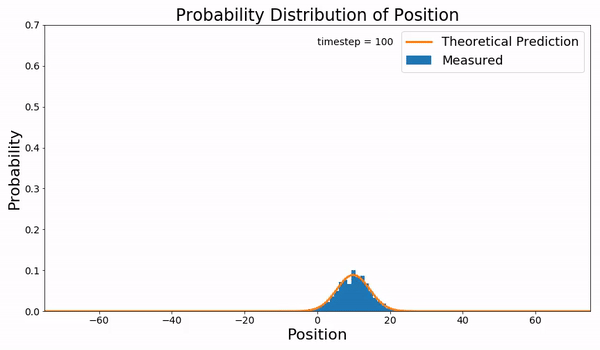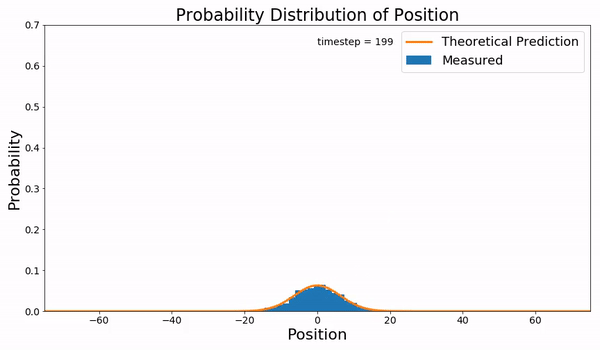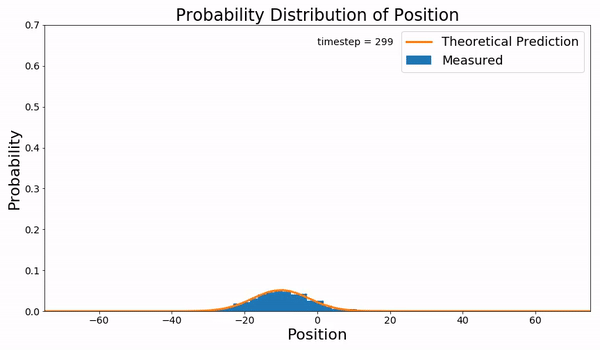
Fokker–Planck Equation
In statistical mechanics and information theory, the Fokker–Planck equation is a partial differential equation that describes the time evolution of the probability density function of the velocity of a particle under the influence of drag (physics), drag forces and random forces, as in Brownian motion. The equation can be generalized to other observables as well. The Fokker–Planck equation has multiple applications in information theory, graph theory, data science, finance, economics etc. It is named after Adriaan Fokker and Max Planck, who described it in 1914 and 1917. It is also known as the Kolmogorov forward equation, after Andrey Kolmogorov, who independently discovered it in 1931. When applied to particle position distributions, it is better known as the Smoluchowski equation (after Marian Smoluchowski), and in this context it is equivalent to the convection–diffusion equation. When applied to particle position and momentum distributions, it is known as the Klein–Kr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |