|
List Of Topics Named After Bernhard Riemann
The German mathematician Bernhard Riemann (1826–1866) is the eponym of many things. "Riemann" (by field) *Riemann bilinear relations * Riemann conditions *Riemann form * Riemann function * Riemann–Hurwitz formula * Riemann matrix * Riemann operator * Riemann singularity theorem ** Riemann-Kempf singularity theorem * Riemann surface ** Compact Riemann surface ** Planar Riemann surface * Cauchy–Riemann manifold ** The tangential Cauchy–Riemann complex *Zariski–Riemann space Analysis * Cauchy–Riemann equations * Riemann integral ** Generalized Riemann integral ** Riemann multiple integral *Riemann invariant * Riemann mapping theorem ** Measurable Riemann mapping theorem * Riemann problem * Riemann solver * Riemann sphere * Riemann–Hilbert correspondence *Riemann–Hilbert problem * Riemann–Lebesgue lemma * Riemann–Liouville integral * Riemann–Roch theorem **Arithmetic Riemann–Roch theorem ** Riemann–Roch theorem for smooth manifolds ** Riemann–Roch theorem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Bernhard Riemann
Georg Friedrich Bernhard Riemann (; 17 September 1826 – 20 July 1866) was a German mathematician who made contributions to analysis, number theory, and differential geometry. In the field of real analysis, he is mostly known for the first rigorous formulation of the integral, the Riemann integral, and his work on Fourier series. His contributions to complex analysis include most notably the introduction of Riemann surfaces, breaking new ground in a natural, geometric treatment of complex analysis. His 1859 paper on the prime-counting function, containing the original statement of the Riemann hypothesis, is regarded as a foundational paper of analytic number theory. Through his pioneering contributions to differential geometry, Riemann laid the foundations of the mathematics of general relativity. He is considered by many to be one of the greatest mathematicians of all time. Biography Early years Riemann was born on 17 September 1826 in Breselenz, a village near D ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Cauchy–Riemann Equations
In the field of complex analysis in mathematics, the Cauchy–Riemann equations, named after Augustin Cauchy and Bernhard Riemann, consist of a system of two partial differential equations which, together with certain continuity and differentiability criteria, form a necessary and sufficient condition for a complex function to be holomorphic (complex differentiable). This system of equations first appeared in the work of Jean le Rond d'Alembert. Later, Leonhard Euler connected this system to the analytic functions. Cauchy then used these equations to construct his theory of functions. Riemann's dissertation on the theory of functions appeared in 1851. The Cauchy–Riemann equations on a pair of real-valued functions of two real variables and are the two equations: Typically ''u'' and ''v'' are taken to be the real and imaginary parts respectively of a complex-valued function of a single complex variable , . Suppose that and are real- differentiable at a point ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Riemann–Liouville Integral
In mathematics, the Riemann–Liouville integral associates with a real function f: \mathbb \rightarrow \mathbb another function of the same kind for each value of the parameter . The integral is a manner of generalization of the repeated antiderivative of in the sense that for positive integer values of , is an iterated antiderivative of of order . The Riemann–Liouville integral is named for Bernhard Riemann and Joseph Liouville, the latter of whom was the first to consider the possibility of fractional calculus in 1832. The operator agrees with the Euler transform, after Leonhard Euler, when applied to analytic functions. It was generalized to arbitrary dimensions by Marcel Riesz, who introduced the Riesz potential. Definition The Riemann–Liouville integral is defined by :I^\alpha f(x) = \frac\int_a^xf(t)(x-t)^\,dt where is the gamma function and is an arbitrary but fixed base point. The integral is well-defined provided is a locally integrable function, and is a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Riemann–Lebesgue Lemma
In mathematics, the Riemann–Lebesgue lemma, named after Bernhard Riemann and Henri Lebesgue, states that the Fourier transform or Laplace transform of an ''L''1 function vanishes at infinity. It is of importance in harmonic analysis and asymptotic analysis. Statement Let f\in L^1(\R^n) be an integrable function, i.e. f\colon\R^n \rightarrow \C is a measurable function such that :\, f\, _ = \int_ , f(x), \mathrmx 0, pick a compactly supported continuous function g such that \, f-g\, _ \leq \varepsilon. Then : \limsup_ , \hat(\xi), \leq \limsup_ \left, \int (f(x)-g(x))\mathrm^ \, \mathrmx\ + \limsup_ \left, \int g(x)\mathrm^ \, \mathrmx\ \leq \varepsilon + 0 = \varepsilon. Because this holds for any \varepsilon > 0, it follows that , \hat(\xi), \to 0 as , \xi, \to\infty . Other versions The Riemann–Lebesgue lemma holds in a variety of other situations. * If f \in L^1 z, \to \infty within the half-plane \mathrm(z) \geq 0. * A version holds for Fourier coefficie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Riemann–Hilbert Problem
In mathematics, Riemann–Hilbert problems, named after Bernhard Riemann and David Hilbert, are a class of problems that arise in the study of differential equations in the complex plane. Several existence theorems for Riemann–Hilbert problems have been produced by Mark Krein, Israel Gohberg and others (see the book by Clancey and Gohberg (1981)). The Riemann problem Suppose that \Sigma is a closed simple contour in the complex plane dividing the plane into two parts denoted by \Sigma_ (the inside) and \Sigma_ (the outside), determined by the index of the contour with respect to a point. The classical problem, considered in Riemann's PhD dissertation (see ), was that of finding a function :M_+(z) = u(z) + i v(z) analytic inside \Sigma_ such that the boundary values of ''M''+ along \Sigma satisfy the equation :a(z)u(z) - b(z)v(z) = c(z) for all z\in \Sigma, where ''a'', ''b'', and ''c'' are given real-valued functions . By the Riemann mapping theorem, it suffices to cons ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Riemann–Hilbert Correspondence
In mathematics, the term Riemann–Hilbert correspondence refers to the correspondence between regular singular flat connections on algebraic vector bundles and representations of the fundamental group, and more generally to one of several generalizations of this. The original setting appearing in Hilbert's twenty-first problem was for the Riemann sphere, where it was about the existence of systems of linear regular differential equations with prescribed monodromy representations. First the Riemann sphere may be replaced by an arbitrary Riemann surface and then, in higher dimensions, Riemann surfaces are replaced by complex manifolds of dimension > 1. There is a correspondence between certain systems of partial differential equations (linear and having very special properties for their solutions) and possible monodromies of their solutions. Such a result was proved for algebraic connections with regular singularities by Pierre Deligne (1970, generalizing existing work in the case ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Riemann Sphere
In mathematics, the Riemann sphere, named after Bernhard Riemann, is a model of the extended complex plane: the complex plane plus one point at infinity. This extended plane represents the extended complex numbers, that is, the complex numbers plus a value \infty for infinity. With the Riemann model, the point \infty is near to very large numbers, just as the point 0 is near to very small numbers. The extended complex numbers are useful in complex analysis because they allow for division by zero in some circumstances, in a way that makes expressions such as 1/0=\infty well-behaved. For example, any rational function on the complex plane can be extended to a holomorphic function on the Riemann sphere, with the poles of the rational function mapping to infinity. More generally, any meromorphic function can be thought of as a holomorphic function whose codomain is the Riemann sphere. In geometry, the Riemann sphere is the prototypical example of a Riemann surface, and is o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Riemann Solver
A Riemann solver is a numerical method used to solve a Riemann problem. They are heavily used in computational fluid dynamics and computational magnetohydrodynamics. Definition Generally speaking, Riemann solvers are specific methods for computing the numerical flux across a discontinuity in the Riemann problem. They form an important part of high-resolution schemes; typically the right and left states for the Riemann problem are calculated using some form of nonlinear reconstruction, such as a flux limiter or a WENO method, and then used as the input for the Riemann solver. Exact solvers Sergei K. Godunov is credited with introducing the first exact Riemann solver for the Euler equations, by extending the previous CIR (Courant-Isaacson-Rees) method to non-linear systems of hyperbolic conservation laws. Modern solvers are able to simulate relativistic effects and magnetic fields. More recent research shows that an exact series solution to the Riemann problem exists, which ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Riemann Problem
A Riemann problem, named after Bernhard Riemann, is a specific initial value problem composed of a conservation equation together with piecewise constant initial data which has a single discontinuity in the domain of interest. The Riemann problem is very useful for the understanding of equations like Euler conservation equations because all properties, such as shocks and rarefaction waves, appear as characteristics in the solution. It also gives an exact solution to some complex nonlinear equations, such as the Euler equations. In numerical analysis, Riemann problems appear in a natural way in finite volume methods for the solution of conservation law equations due to the discreteness of the grid. For that it is widely used in computational fluid dynamics and in computational magnetohydrodynamics simulations. In these fields, Riemann problems are calculated using Riemann solvers. The Riemann problem in linearized gas dynamics As a simple example, we investigate the propertie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Quasiconformal Mapping
In mathematical complex analysis, a quasiconformal mapping, introduced by and named by , is a homeomorphism between plane domains which to first order takes small circles to small ellipses of bounded eccentricity. Intuitively, let ''f'' : ''D'' → ''D''′ be an orientation-preserving homeomorphism between open sets in the plane. If ''f'' is continuously differentiable, then it is ''K''-quasiconformal if the derivative of ''f'' at every point maps circles to ellipses with eccentricity bounded by ''K''. Definition Suppose ''f'' : ''D'' → ''D''′ where ''D'' and ''D''′ are two domains in C. There are a variety of equivalent definitions, depending on the required smoothness of ''f''. If ''f'' is assumed to have continuous partial derivatives, then ''f'' is quasiconformal provided it satisfies the Beltrami equation for some complex valued Lebesgue measurable μ satisfying sup , μ, 0. Then ''f'' satisfies () precisely when it i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
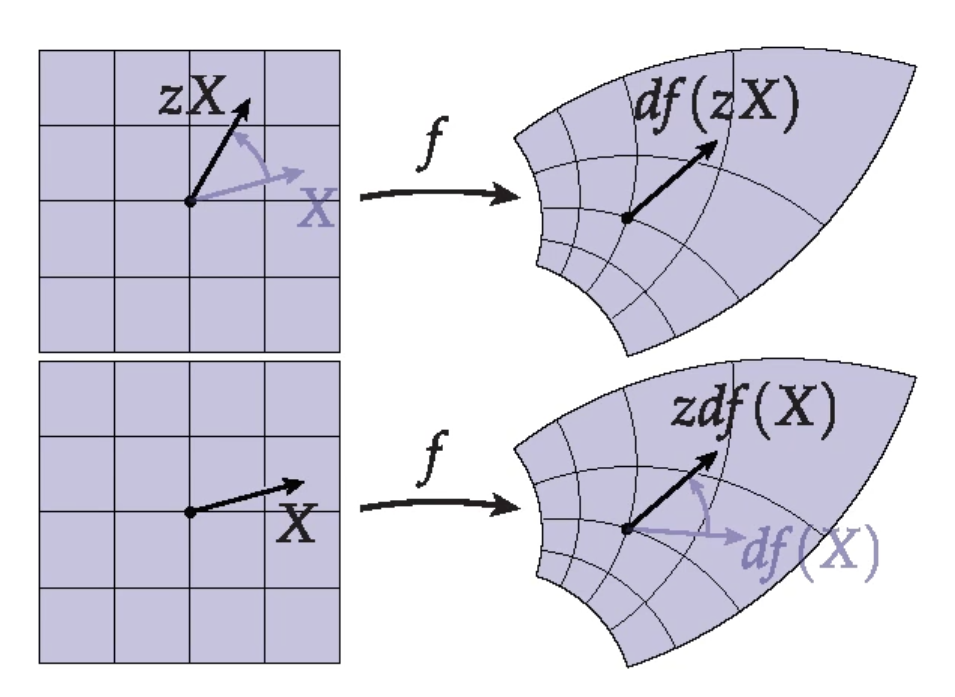
Riemann Mapping Theorem
In complex analysis, the Riemann mapping theorem states that if ''U'' is a non-empty simply connected open subset of the complex number plane C which is not all of C, then there exists a biholomorphic mapping ''f'' (i.e. a bijective holomorphic mapping whose inverse is also holomorphic) from ''U'' onto the open unit disk :D = \. This mapping is known as a Riemann mapping. Intuitively, the condition that ''U'' be simply connected means that ''U'' does not contain any “holes”. The fact that ''f'' is biholomorphic implies that it is a conformal map and therefore angle-preserving. Such a map may be interpreted as preserving the shape of any sufficiently small figure, while possibly rotating and scaling (but not reflecting) it. Henri Poincaré proved that the map ''f'' is essentially unique: if ''z''0 is an element of ''U'' and φ is an arbitrary angle, then there exists precisely one ''f'' as above such that ''f''(''z''0) = 0 and such that the argument of the derivative of ''f'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Riemann Invariant
Riemann invariants are mathematical transformations made on a system of conservation equations to make them more easily solvable. Riemann invariants are constant along the characteristic curves of the partial differential equations where they obtain the name invariant. They were first obtained by Bernhard Riemann in his work on plane waves in gas dynamics. Mathematical theory Consider the set of conservation equations: : l_i\left(A_ \frac +a_\frac \right)+l_j b_j=0 where A_ and a_ are the elements of the matrices \mathbf and \mathbf where l_ and b_ are elements of vectors. It will be asked if it is possible to rewrite this equation to : m_j\left(\beta\frac +\alpha\frac \right)+l_j b_j=0 To do this curves will be introduced in the (x,t) plane defined by the vector field (\alpha,\beta). The term in the brackets will be rewritten in terms of a total derivative where x,t are parametrized as x=X(\eta),t=T(\eta) : \frac=T'\frac+X'\frac comparing the last two equation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |