|
List Of Things Named After Archimedes
Archimedes (c. 287 BC – c. 212 BC) is the eponym of all of the things (and topics) listed below. Mathematical concepts *Archimedean absolute value *Archimedean circle *Archimedean copula *Archimedean group * Archimedean ordered field *Archimedean point *Archimedean property *Archimedean solid *Archimedean spiral *Archimedean tiling * Archimedes' axiom *Archimedes' cattle problem * Archimedes' hat-box theorem *Archimedes constant *Archimedes number *Archimedes' quadruplets *Archimedes Square *Archimedes' twin circles *Heron–Archimedes formula *Non-Archimedean geometry *Non-Archimedean ordered field *Archimedes' ostomachion Physical concepts *Archimedes paradox *Archimedes' principle Technology Things invented by Archimedes * Archimedes' pulley *Archimedes' screw ** Archimedean turbine * Archimedes heat ray *Claw of Archimedes *Trammel of Archimedes Other *Archimedes bridge *Archimede combined cycle power plant * SS Archimedes *Archimedes Group Computer hardwar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Archimedes
Archimedes of Syracuse (;; ) was a Greek mathematician, physicist, engineer, astronomer, and inventor from the ancient city of Syracuse in Sicily. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Considered the greatest mathematician of ancient history, and one of the greatest of all time,* * * * * * * * * * Archimedes anticipated modern calculus and analysis by applying the concept of the infinitely small and the method of exhaustion to derive and rigorously prove a range of geometrical theorems. These include the area of a circle, the surface area and volume of a sphere, the area of an ellipse, the area under a parabola, the volume of a segment of a paraboloid of revolution, the volume of a segment of a hyperboloid of revolution, and the area of a spiral. Heath, Thomas L. 1897. ''Works of Archimedes''. Archimedes' other mathematical achievements include deriving an approximation of pi, defining and in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Archimedes Square
''Ostomachion'', also known as ''loculus Archimedius'' (Archimedes' box in Latin) and also as ''syntomachion'', is a mathematical treatise attributed to Archimedes. This work has survived fragmentarily in an Arabic version and a copy, the ''Archimedes Palimpsest'', of the original ancient Greek text made in Byzantine times.Darling, David (2004). ''The universal book of mathematics: from Abracadabra to Zeno's paradoxes''. John Wiley and Sons, p. 188. The word Ostomachion has as its roots in the Greek Ὀστομάχιον, which means "bone-fight", from ὀστέον (''osteon''), "bone" and μάχη (''mache''), "fight, battle, combat". Note that the manuscripts refer to the word as "Stomachion", an apparent corruption of the original Greek. Ausonius gives us the correct name "Ostomachion" (''quod Graeci ostomachion vocavere,'' "which the Greeks called ostomachion"). The Ostomachion which he describes was a puzzle similar to tangrams and was played perhaps by several persons w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Archimedes Bridge
A submerged floating tunnel (SFT), also known as submerged floating tube bridge (SFTB), suspended tunnel, or Archimedes bridge, is a proposed design for a tunnel that floats in water, supported by its buoyancy (specifically, by employing the hydrostatic thrust, or Archimedes' principle). The tube would be placed underwater, deep enough to avoid water traffic and weather, but not so deep that high water pressure needs to be dealt with; usually a depth of is sufficient. Tether, Cables either anchored to the seabed or to Pontoon (boat), pontoons on the surface would prevent it from floating to the surface or submerging, respectively. Construction The concept of submerged floating tunnels is based on well-known technology applied to pontoon bridge, floating bridges and offshore structures, but the construction is mostly similar to that of Immersed tube, immersed tunnels: After the tube is prefabricated in sections in a dry dock and the sections are moved to the site, one way is to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
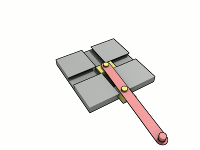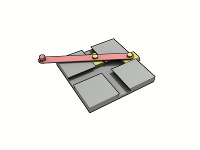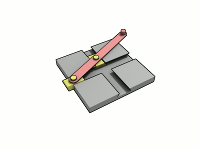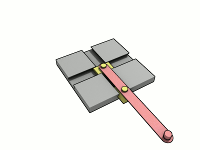
Trammel Of Archimedes
A trammel of Archimedes is a mechanism that generates the shape of an ellipse. () It consists of two shuttles which are confined ("trammeled") to perpendicular channels or rails and a rod which is attached to the shuttles by pivots at fixed positions along the rod. As the shuttles move back and forth, each along its channel, all points on the rod move in elliptical paths. The motion of the rod is termed elliptical motion. The semi-axes ''a'' and ''b'' of the ellipses have lengths equal to the distances from the point on the rod to each of the two pivots. The straight lines described by the pivots are special cases of an ellipse, where the length of one axis is twice the distance between the pivots and that of the other is zero. All points on a circle with a diameter defined by the two pivots reciprocate in such straight lines. This circle corresponds to the smaller circle in a Tusi couple. The point midway between the pivots orbits in a circle around the point where the chan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Claw Of Archimedes
The Claw of Archimedes ( grc, Ἁρπάγη, translit=harpágē, lit=snatcher; also known as the iron hand) was an ancient weapon devised by Archimedes to defend the seaward portion of Syracuse's city wall against amphibious assault. Although its exact nature is unclear, the accounts of ancient historians seem to describe it as a sort of crane equipped with a grappling hook that was able to drop an attacking ship partly down in to the water, then either cause the ship to capsize or suddenly drop it. It was dropped onto enemy ships, which would then swing on to defensive forces and destroy them. These machines featured prominently during the Second Punic War in 214 BC, when the Roman Republic attacked Syracuse with a fleet of 60 quinqueremes under Marcus Claudius Marcellus. When the Roman fleet approached the city walls under cover of darkness, the machines were deployed, sinking many ships and throwing the attack into confusion. Historians such as Livy attributed heavy Ro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Screw Turbine
A screw and a bolt (see '' Differentiation between bolt and screw'' below) are similar types of fastener typically made of metal and characterized by a helical ridge, called a ''male thread'' (external thread). Screws and bolts are used to fasten materials by the engagement of the screw thread with a similar ''female thread'' (internal thread) in a matching part. Screws are often self-threading (also known as self-tapping) where the thread cuts into the material when the screw is turned, creating an internal thread that helps pull fastened materials together and prevents pull-out. There are many screws for a variety of materials; materials commonly fastened by screws include wood, sheet metal, and plastic. Explanation A screw is a combination of simple machines: it is, in essence, an inclined plane wrapped around a central shaft, but the inclined plane (thread) also comes to a sharp edge around the outside, which acts as a wedge as it pushes into the fastened material, and th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Archimedes' Screw
The Archimedes screw, also known as the Archimedean screw, hydrodynamic screw, water screw or Egyptian screw, is one of the earliest hydraulic machines. Using Archimedes screws as water pumps (Archimedes screw pump (ASP) or screw pump) dates back many centuries. As a machine used for pump, transferring water from a low-lying body of water into irrigation ditches, water is pumped by turning a screw-shaped surface inside a pipe. In the modern world, Archimedes screw pumps are widely used in wastewater treatment plants and for dewatering low-lying regions. Screw turbine, Archimedes Screws Turbines (ASTs) are a new form of small hydroelectric powerplant that can be applied even in low head sites. Screw turbine, Archimedes screw generators operate in a wide range of flows (0.01 m^3/s to 14.5 m^3/s) and heads (0.1 m to 10 m), including low heads and moderate flow rates that is not ideal for traditional turbines and not occupied by high performance technologies. The Archimedes screw is a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Archimedes' Principle
Archimedes' principle (also spelled Archimedes's principle) states that the upward buoyant force that is exerted on a body immersed in a fluid, whether fully or partially, is equal to the weight of the fluid that the body displaces. Archimedes' principle is a law of physics fundamental to fluid mechanics. It was formulated by Archimedes of Syracuse. Explanation In ''On Floating Bodies'', Archimedes suggested that (c. 246 BC): Archimedes' principle allows the buoyancy of any floating object partially or fully immersed in a fluid to be calculated. The downward force on the object is simply its weight. The upward, or buoyant, force on the object is that stated by Archimedes' principle above. Thus, the net force on the object is the difference between the magnitudes of the buoyant force and its weight. If this net force is positive, the object rises; if negative, the object sinks; and if zero, the object is neutrally buoyant—that is, it remains in place without either rising ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
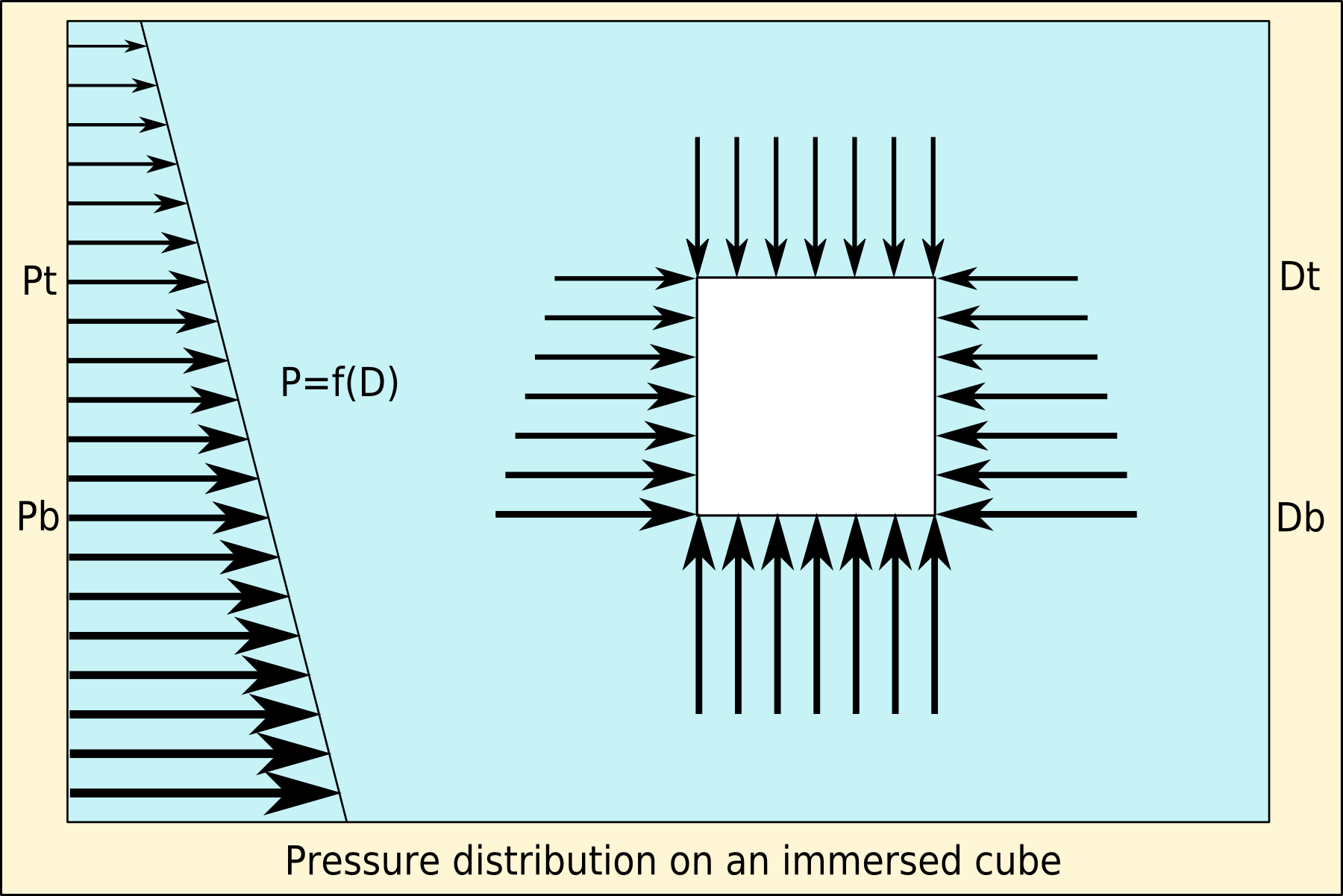
Archimedes Paradox
Vertical pressure variation is the variation in pressure as a function of elevation. Depending on the fluid in question and the context being referred to, it may also vary significantly in dimensions perpendicular to elevation as well, and these variations have relevance in the context of pressure gradient force and its effects. However, the vertical variation is especially significant, as it results from the pull of gravity on the fluid; namely, for the same given fluid, a decrease in elevation within it corresponds to a taller column of fluid weighing down on that point. Basic formula A relatively simple version of the vertical fluid pressure variation is simply that the pressure difference between two elevations is the product of elevation change, gravity, and density. The equation is as follows: \frac = - \rho g , where * is pressure, * is density, * is acceleration of gravity, and * is height. The delta symbol indicates a change in a given variable. Since is negative, an inc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Archimedes' Ostomachion
''Ostomachion'', also known as ''loculus Archimedius'' (Archimedes' box in Latin) and also as ''syntomachion'', is a mathematical treatise attributed to Archimedes. This work has survived fragmentarily in an Arabic version and a copy, the ''Archimedes Palimpsest'', of the original ancient Greek text made in Byzantine times.Darling, David (2004). ''The universal book of mathematics: from Abracadabra to Zeno's paradoxes''. John Wiley and Sons, p. 188. The word Ostomachion has as its roots in the Greek Ὀστομάχιον, which means "bone-fight", from ὀστέον (''osteon''), "bone" and μάχη (''mache''), "fight, battle, combat". Note that the manuscripts refer to the word as "Stomachion", an apparent corruption of the original Greek. Ausonius gives us the correct name "Ostomachion" (''quod Graeci ostomachion vocavere,'' "which the Greeks called ostomachion"). The Ostomachion which he describes was a puzzle similar to tangrams and was played perhaps by several persons w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Non-Archimedean Ordered Field
In mathematics, a non-Archimedean ordered field is an ordered field that does not satisfy the Archimedean property. Examples are the Levi-Civita field, the hyperreal numbers, the surreal numbers, the Dehn field, and the field of rational functions with real coefficients with a suitable order. Definition The Archimedean property is a property of certain ordered fields such as the rational numbers or the real numbers, stating that every two elements are within an integer multiple of each other. If a field contains two positive elements for which this is not true, then must be an infinitesimal, greater than zero but smaller than any integer unit fraction. Therefore, the negation of the Archimedean property is equivalent to the existence of infinitesimals. Applications Hyperreal fields, non-Archimedean ordered fields containing the real numbers as a subfield, may be used to provide a mathematical foundation for nonstandard analysis. Max Dehn used the Dehn field, an example of a non ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
_by_Thomas_Degeorge.png)