|
List Of Spirals
This list of spirals includes named spirals that have been described mathematically. See also * Catherine wheel (firework) * List of spiral galaxies * Parker spiral * Spirangle * Spirograph Spirograph is a geometric drawing device that produces mathematical roulette curves of the variety technically known as hypotrochoids and epitrochoids. The well-known toy version was developed by British engineer Denys Fisher and first sold in ... References {{Spirals Spirals ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spirals
In mathematics, a spiral is a curve which emanates from a point, moving farther away as it revolves around the point. Helices Two major definitions of "spiral" in the American Heritage Dictionary are:Spiral ''American Heritage Dictionary of the English Language'', Houghton Mifflin Company, Fourth Edition, 2009. # a curve on a plane that winds around a fixed center point at a continuously increasing or decreasing distance from the point. # a three-dimensional curve that turns around an axis at a constant or continuously varying distance while moving parallel to the axis; a . The first definition describes a |
Golden Spiral In Rectanglesflip
Golden means made of, or relating to gold. Golden may also refer to: Places United Kingdom *Golden, in the parish of Probus, Cornwall *Golden Cap, Dorset *Golden Square, Soho, London *Golden Valley, a valley on the River Frome in Gloucestershire *Golden Valley, Herefordshire United States *Golden, Colorado, a town West of Denver, county seat of Jefferson County *Golden, Idaho, an unincorporated community *Golden, Illinois, a village *Golden Township, Michigan *Golden, Mississippi, a village *Golden City, Missouri, a city *Golden, Missouri, an unincorporated community *Golden, Nebraska, ghost town in Burt County *Golden Township, Holt County, Nebraska *Golden, New Mexico, a sparsely populated ghost town *Golden, Oregon, an abandoned mining town *Golden, Texas, an unincorporated community *Golden, Utah, a ghost town *Golden, Marshall County, West Virginia, an unincorporated community Elsewhere *Golden, County Tipperary, Ireland, a village on the River Suir *Golden Vale, Munster, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nielsen's Spiral
In mathematics, trigonometric integrals are a family of integrals involving trigonometric functions. Sine integral The different sine integral definitions are \operatorname(x) = \int_0^x\frac\,dt \operatorname(x) = -\int_x^\infty\frac\,dt~. Note that the integrand is the sinc function, and also the zeroth spherical Bessel function. Since is an even entire function (holomorphic over the entire complex plane), is entire, odd, and the integral in its definition can be taken along any path connecting the endpoints. By definition, is the antiderivative of whose value is zero at , and is the antiderivative whose value is zero at . Their difference is given by the Dirichlet integral, \operatorname(x) - \operatorname(x) = \int_0^\infty\frac\,dt = \frac \quad \text \quad \operatorname(x) = \frac + \operatorname(x) ~. In signal processing, the oscillations of the sine integral cause overshoot and ringing artifacts when using the sinc filter, and frequency domain ringing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poinsot's Spirals
In mathematics, Poinsot's spirals are two spirals represented by the polar equations : r = a\ \operatorname (n\theta) : r = a\ \operatorname (n\theta) where csch is the hyperbolic cosecant, and sech is the hyperbolic secant. They are named after the French mathematician Louis Poinsot Louis Poinsot (3 January 1777 – 5 December 1859) was a French mathematician and physicist. Poinsot was the inventor of geometrical mechanics, showing how a system of forces acting on a rigid body could be resolved into a single force and a c .... Examples of the two types of Poinsot's spirals See also * Cotes's spiral References Spirals {{geometry-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cotes's Spiral
Introduction In physics and in the mathematics of plane curves, a Cotes's spiral (also written Cotes' spiral and Cotes spiral) is one of a family of spirals classified by Roger Cotes. Cotes introduces his analysis of these curves as follows: “It is proposed to list the different types of trajectories which bodies can move along when acted on by centripetal forces in the inverse ratio of the cubes of their distances, proceeding from a given place, with given speed, and direction.” (N. b. he does not describe them as spirals). The shape of spirals in the family depends on the parameters. The curves in polar coordinates, (''r'', ''θ''), ''r'' > 0 are defined by one of the following five equations: : \frac = \begin A \cosh(k\theta + \varepsilon) \\ A \exp(k\theta + \varepsilon) \\ A \sinh(k\theta + \varepsilon) \\ A (k\theta + \varepsilon) \\ A \cos(k\theta + \varepsilon) \\ \end ''A'' > 0, ''k'' > 0 and ''ε'' are arbitrary real number constants. ''A'' determines th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
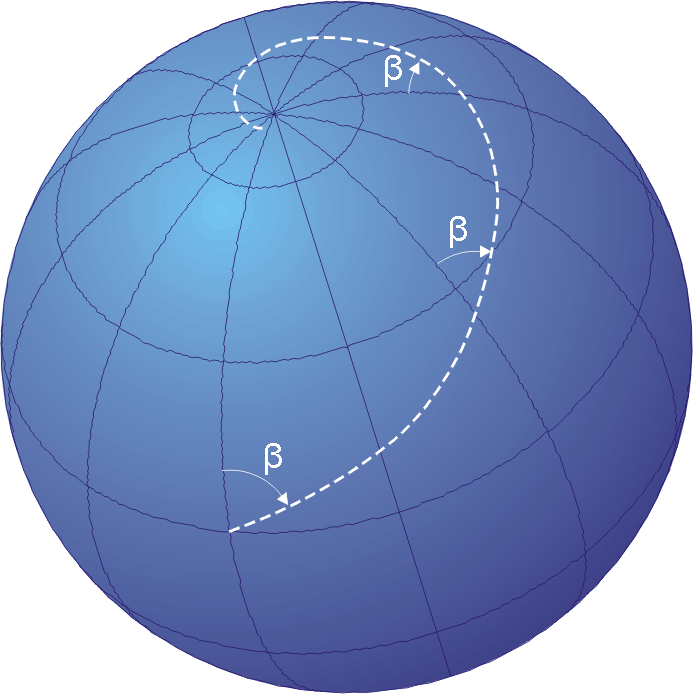
Rhumb Line
In navigation, a rhumb line, rhumb (), or loxodrome is an arc crossing all meridians of longitude at the same angle, that is, a path with constant bearing as measured relative to true north. Introduction The effect of following a rhumb line course on the surface of a globe was first discussed by the Portuguese mathematician Pedro Nunes in 1537, in his ''Treatise in Defense of the Marine Chart'', with further mathematical development by Thomas Harriot in the 1590s. A rhumb line can be contrasted with a great circle, which is the path of shortest distance between two points on the surface of a sphere. On a great circle, the bearing to the destination point does not remain constant. If one were to drive a car along a great circle one would hold the steering wheel fixed, but to follow a rhumb line one would have to turn the wheel, turning it more sharply as the poles are approached. In other words, a great circle is locally "straight" with zero geodesic curvature, whereas a r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Loxodrome
In navigation, a rhumb line, rhumb (), or loxodrome is an arc (geometry), arc crossing all meridian (geography), meridians of longitude at the same angle, that is, a path with constant bearing (navigation), bearing as measured relative to true north. Introduction The effect of following a rhumb line course on the surface of a globe was first discussed by the Portuguese people, Portuguese mathematician Pedro Nunes in 1537, in his ''Treatise in Defense of the Marine Chart'', with further mathematical development by Thomas Harriot in the 1590s. A rhumb line can be contrasted with a great circle, which is the path of shortest distance between two points on the surface of a sphere. On a great circle, the bearing to the destination point does not remain constant. If one were to drive a car along a great circle one would hold the steering wheel fixed, but to follow a rhumb line one would have to turn the wheel, turning it more sharply as the poles are approached. In other words, a g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Helix
A helix () is a shape like a corkscrew or spiral staircase. It is a type of smooth space curve with tangent lines at a constant angle to a fixed axis. Helices are important in biology, as the DNA molecule is formed as two intertwined helices, and many proteins have helical substructures, known as alpha helices. The word ''helix'' comes from the Greek word ''ἕλιξ'', "twisted, curved". A "filled-in" helix – for example, a "spiral" (helical) ramp – is a surface called ''helicoid''. Properties and types The ''pitch'' of a helix is the height of one complete helix turn, measured parallel to the axis of the helix. A double helix consists of two (typically congruent) helices with the same axis, differing by a translation along the axis. A circular helix (i.e. one with constant radius) has constant band curvature and constant torsion. A ''conic helix'', also known as a ''conic spiral'', may be defined as a spiral on a conic surface, with the distance to the apex an expo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Helix
A helix () is a shape like a corkscrew or spiral staircase. It is a type of smooth space curve with tangent lines at a constant angle to a fixed axis. Helices are important in biology, as the DNA molecule is formed as two intertwined helices, and many proteins have helical substructures, known as alpha helices. The word ''helix'' comes from the Greek word ''ἕλιξ'', "twisted, curved". A "filled-in" helix – for example, a "spiral" (helical) ramp – is a surface called ''helicoid''. Properties and types The ''pitch'' of a helix is the height of one complete helix turn, measured parallel to the axis of the helix. A double helix consists of two (typically congruent) helices with the same axis, differing by a translation along the axis. A circular helix (i.e. one with constant radius) has constant band curvature and constant torsion. A ''conic helix'', also known as a ''conic spiral'', may be defined as a spiral on a conic surface, with the distance to the apex an expo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Involute
In mathematics, an involute (also known as an evolvent) is a particular type of curve that is dependent on another shape or curve. An involute of a curve is the locus of a point on a piece of taut string as the string is either unwrapped from or wrapped around the curve. It is a class of curves coming under the roulette family of curves. The evolute of an involute is the original curve. The notions of the involute and evolute of a curve were introduced by Christiaan Huygens in his work titled '' Horologium oscillatorium sive de motu pendulorum ad horologia aptato demonstrationes geometricae'' (1673). Involute of a parameterized curve Let \vec c(t),\; t\in _1,t_2 be a regular curve in the plane with its curvature nowhere 0 and a\in (t_1,t_2), then the curve with the parametric representation \vec C_a(t)=\vec c(t) -\frac\; \int_a^t, \vec c'(w), \; dw is an ''involute'' of the given curve. Adding an arbitrary but fixed number l_0 to the integral \Bigl(\int_a^t, \ve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |