involute

In mathematics, an involute (also known as an evolvent) is a particular type of curve that is dependent on another shape or curve. An involute of a curve is the locus of a point on a piece of taut string as the string is either unwrapped from or wrapped around the curve.

It is a class of curves coming under the roulette family of curves.

The evolute of an involute is the original curve.

The notions of the involute and evolute of a curve were introduced by Christiaan Huygens in his work titled '' Horologium oscillatorium sive de motu pendulorum ad horologia aptato demonstrationes geometricae'' (1673).

Involute of a parameterized curve

Let \vec c(t),\; t\in _1,t_2 be a regular curve in the plane with its curvature nowhere 0 and $a\in (t_1,t_2)$, then the curve with the parametric representation

$\vec C_a(t)=\vec c(t) -\frac\; \int_a^t, \vec c'(w), \; dw$

is an ''involute'' of the given curve.

Adding an arbitrary but fixed number $l_0$ to the integral $\Bigl(\int_a^t, \vec c'(w), \; dw\Bigr)$ results in an involute corresponding to a string extended by $l_0$ (like a ball of wool yarn having some length of thread already hanging before it is unwound). Hence, the involute can be varied by constant $a$ and/or adding a number to the integral (see Involutes of a semicubic parabola).

If $\vec c(t)=(x(t),y(t))^T$ one gets

:$\begin X(t) &= x(t) - \frac \int_a^t \sqrt \,dw \\ Y(t) &= y(t) - \frac \int_a^t \sqrt \,dw \; . \end$

Properties of involutes

In order to derive properties of a regular curve it is advantageous to suppose the arc length $s$ to be the parameter of the given curve, which lead to the following simplifications: $\;, \vec c'(s), =1\;$ and $\;\vec c''(s)=\kappa(s)\vec n(s)\;$, with $\kappa$ the curvature and $\vec n$ the unit normal. One gets for the involute:

:$\vec C_a(s)=\vec c(s) -\vec c'(s)(s-a)\$ and
:$\vec C_a'(s)=-\vec c''(s)(s-a)=-\kappa(s)\vec n(s)(s-a)\;$
and the statement:
*At point $\vec C_a(a)$ the involute is ''not regular'' (because $, \vec C_a'(a), =0$ ),
and from $\; \vec C_a'(s)\cdot\vec c'(s)=0 \;$ follows:
* The normal of the involute at point $\vec C_a(s)$ is the tangent of the given curve at point $\vec c(s)$.
* The involutes are parallel curves, because of $\vec C_a(s)=\vec C_0(s)+a\vec c'(s)$ and the fact, that $\vec c'(s)$ is the unit normal at $\vec C_0(s)$.

Examples

Involutes of a circle

For a circle with parametric representation $(r\cos(t), r\sin(t))$, one has
$\vec c'(t) = (-r\sin t, r\cos t)$.
Hence $, \vec c'(t), = r$, and the path length is $r(t - a)$.

Evaluating the above given equation of the involute, one gets
:$\begin X(t) &= r(\cos t + (t - a)\sin t)\\ Y(t) &= r(\sin t - (t - a)\cos t) \end$
for the parametric equation of the involute of the circle.

The $a$ term is optional; it serves to set the start location of the curve on the circle. The figure shows involutes for $a = -0.5$ (green), $a = 0$ (red), $a = 0.5$ (purple) and $a = 1$ (light blue). The involutes look like Archimedean spirals, but they are actually not.

The arc length for $a=0$ and $0 \le t \le t_2$ of the involute is
: $L = \frac t_2^2.$

Involutes of a semicubic parabola

The parametric equation $\vec c(t) = (\tfrac, \tfrac)$ describes a semicubical parabola. From $\vec c'(t) = (t^2, t)$ one gets $, \vec c'(t), = t\sqrt$ and $\int_0^t w\sqrt\,dw = \frac\sqrt^3 - \frac13$. Extending the string by $l_0=$ extensively simplifies further calculation, and one gets
: $\begin X(t)&= -\frac\\ Y(t) &= \frac - \frac.\end$

Eliminating yields $Y = \fracX^2 - \frac,$ showing that this involute is a parabola.

The other involutes are thus parallel curves of a parabola, and are not parabolas, as they are curves of degree six (See ).

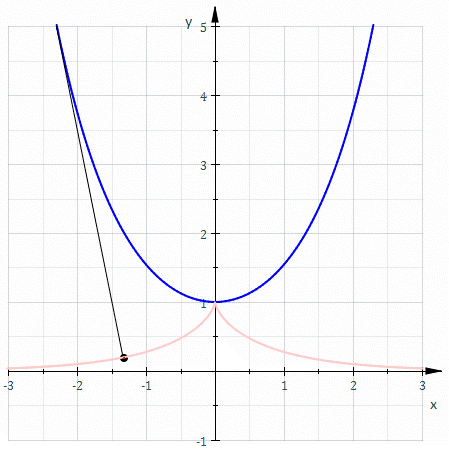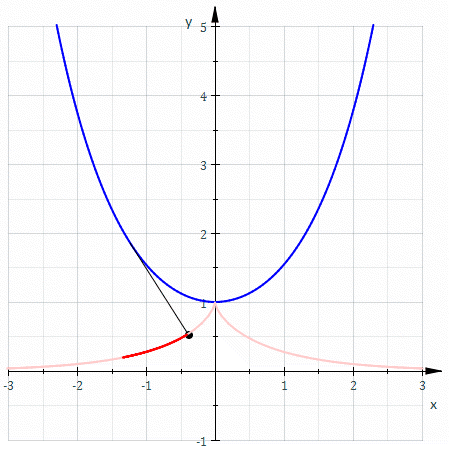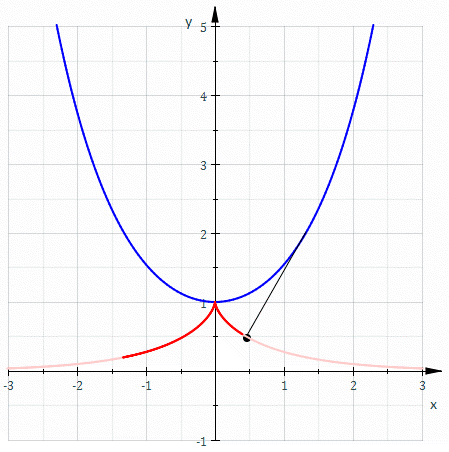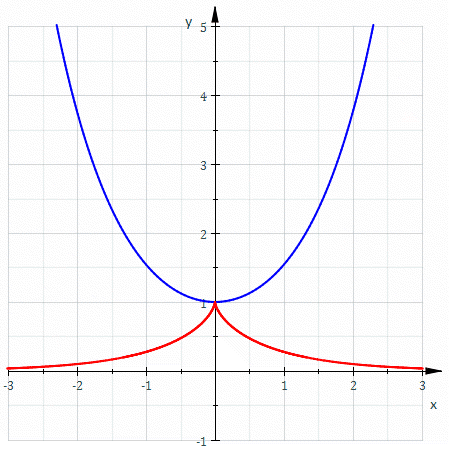
Involutes of a catenary

For the catenary $(t, \cosh t)$, the tangent vector is $\vec c'(t) = (1, \sinh t)$, and, as $1 + \sinh^2 t =\cosh^2 t,$ its length is $, \vec c'(t), = \cosh t$. Thus the arc length from the point is $\textstyle\int_0^t \cosh w\,dw = \sinh t.$

Hence the involute starting from is parametrized by
: $(t - \tanh t, 1/\cosh t),$
and is thus a tractrix.

The other involutes are not tractrices, as they are parallel curves of a tractrix.

Involutes of a cycloid

The parametric representation $\vec c(t) = (t - \sin t, 1 - \cos t)$ describes a cycloid. From $\vec c'(t) = (1 - \cos t, \sin t)$, one gets (after having used some trigonometric formulas)
:$, \vec c'(t), = 2\sin\frac,$
and
:$\int_\pi^t 2\sin\frac\,dw = -4\cos\frac.$

Hence the equations of the corresponding involute are
: $X(t) = t + \sin t,$
: $Y(t) = 3 + \cos t,$
which describe the shifted red cycloid of the diagram. Hence

* The involutes of the cycloid $(t - \sin t, 1 - \cos t)$ are parallel curves of the cycloid
: $(t + \sin t, 3 + \cos t).$
(Parallel curves of a cycloid are not cycloids.)

Involute and evolute

The evolute of a given curve $c_0$ consists of the curvature centers of $c_0$. Between involutes and evolutes the following statement holds:

:''A curve is the evolute of any of its involutes.''

Application

The most common profiles of modern gear teeth are involutes of a circle. In an involute gear system the teeth of two meshing gears contact at a single instantaneous point that follows along a single straight line of action. The forces exerted the contacting teeth exert on each other also follow this line, and are normal to the teeth. The involute gear system maintaining these conditions follows the fundamental law of gearing: the ratio of angular velocities between the two gears must remain constant throughout.

With teeth of other shapes, the relative speeds and forces rise and fall as successive teeth engage, resulting in vibration, noise, and excessive wear. For this reason, nearly all modern planar gear systems are either involute or the related cycloidal gear system.V. G. A. Goss (2013) "Application of analytical geometry to the shape of gear teeth", Resonance 18(9): 817 to 3
Springerlink
(subscription required).

The involute of a circle is also an important shape in gas compressing, as a scroll compressor can be built based on this shape. Scroll compressors make less sound than conventional compressors and have proven to be quite efficient.

The High Flux Isotope Reactor uses involute-shaped fuel elements, since these allow a constant-width channel between them for coolant.

See also

* Evolute
* Scroll compressor
* Involute gear
* Roulette (curve)
* Envelope (mathematics)

References

External links

Involute
at MathWorld

{{Differential transforms of plane curves
Differential geometry
Roulettes (curve)