|
Semicubical Parabola
In mathematics, a cuspidal cubic or semicubical parabola is an algebraic plane curve that has an implicit equation of the form : y^2 - a^2 x^3 = 0 (with ) in some Cartesian coordinate system. Solving for leads to the ''explicit form'' : y = \pm a x^, which imply that every real point satisfies . The exponent explains the term ''semicubical parabola''. (A parabola can be described by the equation .) Solving the implicit equation for yields a second ''explicit form'' :x = \left(\frac\right)^. The parametric equation : \quad x = t^2, \quad y = a t^3 can also be deduced from the implicit equation by putting t = \frac. . The semicubical parabolas have a cuspidal singularity; hence the name of ''cuspidal cubic''. The arc length of the curve was calculated by the English mathematician William Neile and published in 1657 (see section History). Properties of semicubical parabolas Similarity Any semicubical parabola (t^2,at^3) is similar to the ''semicubical unit parabola'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integration By Substitution
In calculus, integration by substitution, also known as ''u''-substitution, reverse chain rule or change of variables, is a method for evaluating integrals and antiderivatives. It is the counterpart to the chain rule for differentiation, and can loosely be thought of as using the chain rule "backwards". Substitution for a single variable Introduction Before stating the result rigorously, consider a simple case using indefinite integrals. Compute \textstyle\int(2x^3+1)^7(x^2)\,dx. Set u=2x^3+1. This means \textstyle\frac=6x^2, or in differential form, du=6x^2\,dx. Now :\int(2x^3 +1)^7(x^2)\,dx = \frac\int\underbrace_\underbrace_=\frac\int u^\,du=\frac\left(\fracu^\right)+C=\frac(2x^3+1)^+C, where C is an arbitrary constant of integration. This procedure is frequently used, but not all integrals are of a form that permits its use. In any event, the result should be verified by differentiating and comparing to the original integrand. :\frac\left frac(2x^3+1)^+C\right\f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
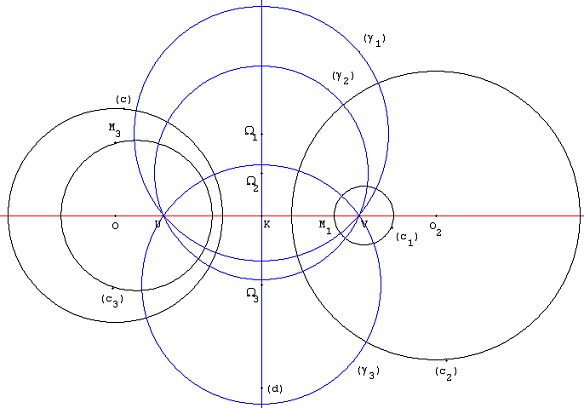
Circle
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is constant. The distance between any point of the circle and the centre is called the radius. Usually, the radius is required to be a positive number. A circle with r=0 (a single point) is a degenerate case. This article is about circles in Euclidean geometry, and, in particular, the Euclidean plane, except where otherwise noted. Specifically, a circle is a simple closed curve that divides the plane into two regions: an interior and an exterior. In everyday use, the term "circle" may be used interchangeably to refer to either the boundary of the figure, or to the whole figure including its interior; in strict technical usage, the circle is only the boundary and the whole figure is called a '' disc''. A circle may also be defined as a special ki ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Line (geometry)
In geometry, a line is an infinitely long object with no width, depth, or curvature. Thus, lines are one-dimensional objects, though they may exist in two, three, or higher dimension spaces. The word ''line'' may also refer to a line segment in everyday life, which has two points to denote its ends. Lines can be referred by two points that lay on it (e.g., \overleftrightarrow) or by a single letter (e.g., \ell). Euclid described a line as "breadthless length" which "lies evenly with respect to the points on itself"; he introduced several postulates as basic unprovable properties from which he constructed all of geometry, which is now called Euclidean geometry to avoid confusion with other geometries which have been introduced since the end of the 19th century (such as non-Euclidean, projective and affine geometry). In modern mathematics, given the multitude of geometries, the concept of a line is closely tied to the way the geometry is described. For instance, in analytic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Curve
In mathematics, an affine algebraic plane curve is the zero set of a polynomial in two variables. A projective algebraic plane curve is the zero set in a projective plane of a homogeneous polynomial in three variables. An affine algebraic plane curve can be completed in a projective algebraic plane curve by homogenizing its defining polynomial. Conversely, a projective algebraic plane curve of homogeneous equation can be restricted to the affine algebraic plane curve of equation . These two operations are each inverse to the other; therefore, the phrase algebraic plane curve is often used without specifying explicitly whether it is the affine or the projective case that is considered. More generally, an algebraic curve is an algebraic variety of dimension one. Equivalently, an algebraic curve is an algebraic variety that is birationally equivalent to an algebraic plane curve. If the curve is contained in an affine space or a projective space, one can take a projection for such a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cycloid
In geometry, a cycloid is the curve traced by a point on a circle as it rolls along a straight line without slipping. A cycloid is a specific form of trochoid and is an example of a roulette, a curve generated by a curve rolling on another curve. The cycloid, with the cusps pointing upward, is the curve of fastest descent under uniform gravity (the brachistochrone curve). It is also the form of a curve for which the period of an object in simple harmonic motion (rolling up and down repetitively) along the curve does not depend on the object's starting position (the tautochrone curve). History The cycloid has been called "The Helen of Geometers" as it caused frequent quarrels among 17th-century mathematicians. Historians of mathematics have proposed several candidates for the discoverer of the cycloid. Mathematical historian Paul Tannery cited similar work by the Syrian philosopher Iamblichus as evidence that the curve was known in antiquity. English mathematician John Wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logarithmic Spiral
A logarithmic spiral, equiangular spiral, or growth spiral is a self-similar spiral curve that often appears in nature. The first to describe a logarithmic spiral was Albrecht Dürer (1525) who called it an "eternal line" ("ewige Linie"). More than a century later, the curve was discussed by Descartes (1638), and later extensively investigated by Jacob Bernoulli, who called it ''Spira mirabilis'', "the marvelous spiral". The logarithmic spiral can be distinguished from the Archimedean spiral by the fact that the distances between the turnings of a logarithmic spiral increase in geometric progression, while in an Archimedean spiral these distances are constant. Definition In polar coordinates (r, \varphi) the logarithmic spiral can be written as r = ae^,\quad \varphi \in \R, or \varphi = \frac \ln \frac, with e being the base of natural logarithms, and a > 0, k\ne 0 being real constants. In Cartesian coordinates The logarithmic spiral with the polar equation r = a e^ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arc Length
ARC may refer to: Business * Aircraft Radio Corporation, a major avionics manufacturer from the 1920s to the '50s * Airlines Reporting Corporation, an airline-owned company that provides ticket distribution, reporting, and settlement services * Airport Regions Conference, a European organization of major airports * Amalgamated Roadstone Corporation, a British stone quarrying company * American Record Company (1904–1908, re-activated 1979), one of two United States record labels by this name * American Record Corporation (1929–1938), a United States record label also known as American Record Company * ARC (American Recording Company) (1978-present), a vanity label for Earth, Wind & Fire * ARC Document Solutions, a company based in California, formerly American Reprographics Company * Amey Roadstone Construction, a former British construction company * Aqaba Railway Corporation, a freight railway in Jordan * ARC/Architectural Resources Cambridge, Inc., Cambridge, Massachusett ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
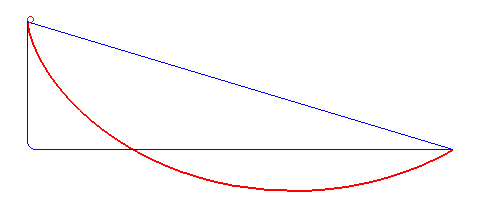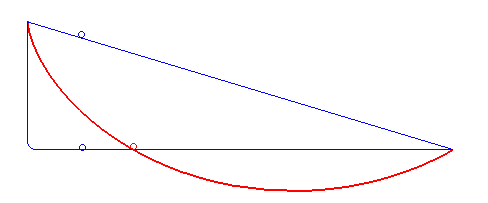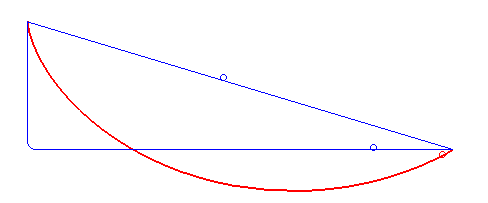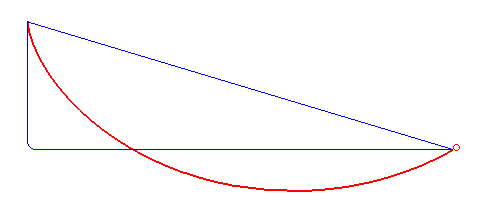
Brachistochrone Curve
In physics and mathematics, a brachistochrone curve (), or curve of fastest descent, is the one lying on the plane between a point ''A'' and a lower point ''B'', where ''B'' is not directly below ''A'', on which a bead slides frictionlessly under the influence of a uniform gravitational field to a given end point in the shortest time. The problem was posed by Johann Bernoulli in 1696. The brachistochrone curve is the same shape as the tautochrone curve; both are cycloids. However, the portion of the cycloid used for each of the two varies. More specifically, the brachistochrone can use up to a complete rotation of the cycloid (at the limit when A and B are at the same level), but always starts at a cusp. In contrast, the tautochrone problem can use only up to the first half rotation, and always ends at the horizontal.Stewart, James. "Section 10.1 - Curves Defined by Parametric Equations." ''Calculus: Early Transcendentals''. 7th ed. Belmont, CA: Thomson Brooks/Cole, 2012. 640. Pri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tautochrone Curve
A tautochrone or isochrone curve (from Greek prefixes tauto- meaning ''same'' or iso- ''equal'', and chrono ''time'') is the curve for which the time taken by an object sliding without friction in uniform gravity to its lowest point is independent of its starting point on the curve. The curve is a cycloid, and the time is equal to π times the square root of the radius (of the circle which generates the cycloid) over the acceleration of gravity. The tautochrone curve is related to the brachistochrone curve, which is also a cycloid. The tautochrone problem The tautochrone problem, the attempt to identify this curve, was solved by Christiaan Huygens in 1659. He proved geometrically in his ''Horologium Oscillatorium'', originally published in 1673, that the curve is a cycloid. The cycloid is given by a point on a circle of radius r tracing a curve as the circle rolls along the x axis, as: \begin x &= r(\theta - \sin \theta) \\ y &= r(1 - \cos \theta), \end Huygens al ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homogeneous Coordinates
In mathematics, homogeneous coordinates or projective coordinates, introduced by August Ferdinand Möbius in his 1827 work , are a system of coordinates used in projective geometry, just as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points, including points at infinity, can be represented using finite coordinates. Formulas involving homogeneous coordinates are often simpler and more symmetric than their Cartesian counterparts. Homogeneous coordinates have a range of applications, including computer graphics and 3D computer vision, where they allow affine transformations and, in general, projective transformations to be easily represented by a matrix. If homogeneous coordinates of a point are multiplied by a non-zero scalar then the resulting coordinates represent the same point. Since homogeneous coordinates are also given to points at infinity, the number of coordinates required to allow this extension is one more than ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projective Map
In projective geometry, a homography is an isomorphism of projective spaces, induced by an isomorphism of the vector spaces from which the projective spaces derive. It is a bijection that maps lines to lines, and thus a collineation. In general, some collineations are not homographies, but the fundamental theorem of projective geometry asserts that is not so in the case of real projective spaces of dimension at least two. Synonyms include projectivity, projective transformation, and projective collineation. Historically, homographies (and projective spaces) have been introduced to study perspective and projections in Euclidean geometry, and the term ''homography'', which, etymologically, roughly means "similar drawing", dates from this time. At the end of the 19th century, formal definitions of projective spaces were introduced, which differed from extending Euclidean or affine spaces by adding points at infinity. The term "projective transformation" originated in these abst ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |