|
List Of Numeral System Topics
This is a list of Wikipedia articles on topics of numeral system and "numeric representations" See also: computer numbering formats and number names. Arranged by base * Radix, radix point, mixed radix, base (mathematics) * Unary numeral system (base 1) ** * Binary numeral system (base 2) * Negative base numeral system (base −2) * Ternary numeral system numeral system (base 3) * Balanced ternary numeral system (base 3) * Negative base numeral system (base −3) * Quaternary numeral system (base 4) * Quater-imaginary base (base 2) * Quinary numeral system (base 5) ** * Senary numeral system (base 6) * Septenary numeral system (base 7) * Octal numeral system (base 8) * Nonary (novenary) numeral system (base 9) * Decimal (denary) numeral system (base 10) ** * Negative base numeral system (base −10) * Duodecimal (dozenal) numeral system (base 12) * Hexadecimal numeral system (base 16) * Vigesimal numeral system (base 20) * Sexagesimal Sexagesimal, also known as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numeral System
A numeral system (or system of numeration) is a writing system for expressing numbers; that is, a mathematical notation for representing numbers of a given set, using digits or other symbols in a consistent manner. The same sequence of symbols may represent different numbers in different numeral systems. For example, "11" represents the number ''eleven'' in the decimal numeral system (used in common life), the number ''three'' in the binary numeral system (used in computers), and the number ''two'' in the unary numeral system (e.g. used in tallying scores). The number the numeral represents is called its value. Not all number systems can represent all numbers that are considered in the modern days; for example, Roman numerals have no zero. Ideally, a numeral system will: *Represent a useful set of numbers (e.g. all integers, or rational numbers) *Give every number represented a unique representation (or at least a standard representation) *Reflect the algebraic and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quater-imaginary Base
The quater-imaginary numeral system is a numeral system, first proposed by Donald Knuth in 1960. Unlike standard numeral systems, which use an integer (such as 10 in decimal, or 2 in binary) as their bases, it uses the imaginary number 2''i'' (equivalent to \sqrt) as its base. It is able to (almost) uniquely represent every complex number using only the digits 0, 1, 2, and 3. Numbers less than zero, which are ordinarily represented with a minus sign, are representable as digit strings in quater-imaginary; for example, the number −1 is represented as "103" in quater-imaginary notation. Decomposing the quater-imaginary In a positional system with base b, \ldots d_3d_2d_1d_0.d_d_d_\ldots represents\dots + d_3\cdot b^3+d_2\cdot b^2+d_1\cdot b+d_0+d_\cdot b^+d_\cdot b^+d_\cdot b^\dots In this numeral system, b = 2i, and because (2i)^2=-4, the entire series of powers can be separated into two different series, so that it simplifies to \begin & dots+d_4\cdot(-4)^2 +d_2\cdot(-4) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sexagesimal
Sexagesimal, also known as base 60 or sexagenary, is a numeral system with sixty as its base. It originated with the ancient Sumerians in the 3rd millennium BC, was passed down to the ancient Babylonians, and is still used—in a modified form—for measuring time, angles, and geographic coordinates. The number 60, a superior highly composite number, has twelve factors, namely 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60, of which 2, 3, and 5 are prime numbers. With so many factors, many fractions involving sexagesimal numbers are simplified. For example, one hour can be divided evenly into sections of 30 minutes, 20 minutes, 15 minutes, 12 minutes, 10 minutes, 6 minutes, 5 minutes, 4 minutes, 3 minutes, 2 minutes, and 1 minute. 60 is the smallest number that is divisible by every number from 1 to 6; that is, it is the lowest common multiple of 1, 2, 3, 4, 5, and 6. ''In this article, all sexagesimal digits are represented as decimal numbers, except where otherwise noted. Fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vigesimal
vigesimal () or base-20 (base-score) numeral system is based on twenty (in the same way in which the decimal numeral system is based on ten). '' Vigesimal'' is derived from the Latin adjective '' vicesimus'', meaning 'twentieth'. Places In a vigesimal place system, twenty individual numerals (or digit symbols) are used, ten more than in the usual decimal system. One modern method of finding the extra needed symbols is to write ten as the letter (the 20 means base ), to write nineteen as , and the numbers between with the corresponding letters of the alphabet. This is similar to the common computer-science practice of writing hexadecimal numerals over 9 with the letters "A–F". Another less common method skips over the letter "I", in order to avoid confusion between I20 as eighteen and one, so that the number eighteen is written as J20, and nineteen is written as K20. The number twenty is written as . According to this notation: : is equivalent to forty in decimal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hexadecimal
In mathematics and computing, the hexadecimal (also base-16 or simply hex) numeral system is a positional numeral system that represents numbers using a radix (base) of 16. Unlike the decimal system representing numbers using 10 symbols, hexadecimal uses 16 distinct symbols, most often the symbols "0"–"9" to represent values 0 to 9, and "A"–"F" (or alternatively "a"–"f") to represent values from 10 to 15. Software developers and system designers widely use hexadecimal numbers because they provide a human-friendly representation of binary-coded values. Each hexadecimal digit represents four bits (binary digits), also known as a nibble (or nybble). For example, an 8-bit byte can have values ranging from 00000000 to 11111111 in binary form, which can be conveniently represented as 00 to FF in hexadecimal. In mathematics, a subscript is typically used to specify the base. For example, the decimal value would be expressed in hexadecimal as . In programming, a number ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Duodecimal
The duodecimal system (also known as base 12, dozenal, or, rarely, uncial) is a positional notation numeral system using twelve as its base. The number twelve (that is, the number written as "12" in the decimal numerical system) is instead written as "10" in duodecimal (meaning "1 dozen and 0 units", instead of "1 ten and 0 units"), whereas the digit string "12" means "1 dozen and 2 units" (decimal 14). Similarly, in duodecimal, "100" means "1 gross", "1000" means "1 great gross", and "0.1" means "1 twelfth" (instead of their decimal meanings "1 hundred", "1 thousand", and "1 tenth", respectively). Various symbols have been used to stand for ten and eleven in duodecimal notation; this page uses and , as in hexadecimal, which make a duodecimal count from zero to twelve read 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, , , 10. The Dozenal Societies of America and Great Britain (organisations promoting the use of duodecimal) use turned digits in their published ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Decimal
The decimal numeral system (also called the base-ten positional numeral system and denary or decanary) is the standard system for denoting integer and non-integer numbers. It is the extension to non-integer numbers of the Hindu–Arabic numeral system. The way of denoting numbers in the decimal system is often referred to as ''decimal notation''. A ''decimal numeral'' (also often just ''decimal'' or, less correctly, ''decimal number''), refers generally to the notation of a number in the decimal numeral system. Decimals may sometimes be identified by a decimal separator (usually "." or "," as in or ). ''Decimal'' may also refer specifically to the digits after the decimal separator, such as in " is the approximation of to ''two decimals''". Zero-digits after a decimal separator serve the purpose of signifying the precision of a value. The numbers that may be represented in the decimal system are the decimal fractions. That is, fractions of the form , where is an inte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonary
A ternary numeral system (also called base 3 or trinary) has three as its base. Analogous to a bit, a ternary digit is a trit (trinary digit). One trit is equivalent to log2 3 (about 1.58496) bits of information. Although ''ternary'' most often refers to a system in which the three digits are all non–negative numbers; specifically , , and , the adjective also lends its name to the balanced ternary system; comprising the digits −1, 0 and +1, used in comparison logic and ternary computers. Comparison to other bases Representations of integer numbers in ternary do not get uncomfortably lengthy as quickly as in binary. For example, decimal 365 or senary 1405 corresponds to binary 101101101 (nine digits) and to ternary 111112 (six digits). However, they are still far less compact than the corresponding representations in bases such as decimalsee below for a compact way to codify ternary using nonary (base 9) and septemvigesimal (base 27). As for rational n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Octal
The octal numeral system, or oct for short, is the radix, base-8 number system, and uses the Numerical digit, digits 0 to 7. This is to say that 10octal represents eight and 100octal represents sixty-four. However, English, like most languages, uses a Base 10, base-10 number system, hence a true octal system might use different vocabulary. In the decimal system, each place is a power of ten. For example: : \mathbf_ = \mathbf \times 10^1 + \mathbf \times 10^0 In the octal system, each place is a power of eight. For example: : \mathbf_8 = \mathbf \times 8^2 + \mathbf \times 8^1 + \mathbf \times 8^0 By performing the calculation above in the familiar decimal system, we see why 112 in octal is equal to 64+8+2=74 in decimal. Octal numerals can be easily converted from Binary numeral system, binary representations (similar to a quaternary numeral system) by grouping consecutive binary digits into groups of three (starting from the right, for integers). For example, the binary repr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Septenary
There are many different numeral systems, that is, writing systems for expressing numbers. By culture / time period By type of notation Numeral systems are classified here as to whether they use positional notation (also known as place-value notation), and further categorized by radix or base. Standard positional numeral systems The common names are derived Hexadecimal#Etymology, somewhat arbitrarily from a mix of Latin and Greek language, Greek, in some cases including roots from both languages within a single name. There have been some proposals for standardisation. Non-standard positional numeral systems Bijective numeration Signed-digit representation Negative bases The common names of the negative base numeral systems are formed using the prefix ''nega-'', giving names such as: Complex-base system, Complex bases Non-integer representation, Non-integer bases p-adic number, ''n''-adic number Mixed radix * Factorial number system * Even double factorial ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Senary
A senary () numeral system (also known as base-6, heximal, or seximal) has 6, six as its radix, base. It has been adopted independently by a small number of cultures. Like decimal, it is a semiprime, though it is unique as the product of the only two consecutive numbers that are both prime (2 and 3). As six is a superior highly composite number, many of the arguments made in favor of the duodecimal system also apply to senary. In turn, the logic, senary logic refers to an extension of Jan Łukasiewicz's and Stephen Cole Kleene's ternary logic systems adjusted to explain the logic of statistical tests and missing data patterns in sciences using empirical methods. Formal definition The standard Set (mathematics), set of digits in senary is given by \mathcal_6 = \lbrace 0, 1, 2, 3, 4, 5\rbrace, with a linear order 0 < 1 < 2 < 3 < 4 < 5. Let be the Kleene closure of , where is the operation of string concatena ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
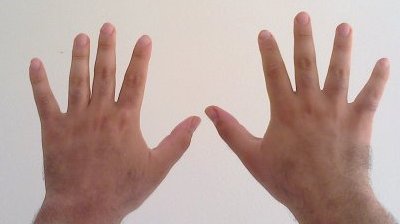
Quinary
Quinary (base-5 or pental) is a numeral system with five as the base. A possible origination of a quinary system is that there are five digits on either hand. In the quinary place system, five numerals, from 0 to 4, are used to represent any real number. According to this method, five is written as 10, twenty-five is written as 100 and sixty is written as 220. As five is a prime number, only the reciprocals of the powers of five terminate, although its location between two highly composite numbers ( 4 and 6) guarantees that many recurring fractions have relatively short periods. Today, the main usage of base 5 is as a biquinary system, which is decimal using five as a sub-base. Another example of a sub-base system, is sexagesimal, base 60, which used 10 as a sub-base. Each quinary digit can hold log25 (approx. 2.32) bits of information. Comparison to other radices Usage Many languagesHarald Hammarström, Rarities in Numeral Systems: "Bases 5, 10, and 20 are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |