|
List Of Logarithm Topics
{{Short description, None This is a list of logarithm topics, by Wikipedia page. See also the list of exponential topics. * Acoustic power * Antilogarithm * Apparent magnitude * Baker's theorem * Bel (unit), Bel * Benford's law * Binary logarithm * Bode plot * Henry Briggs (mathematician), Henry Briggs * Bygrave slide rule * Cologarithm * Common logarithm * Complex logarithm * Discrete logarithm ** Discrete logarithm records * e (mathematical constant), e ** Representations of e * El Gamal discrete log cryptosystem * Harmonic series (mathematics), Harmonic series * History of logarithms * Hyperbolic sector * Iterated logarithm * Otis King * Law of the iterated logarithm * Linear form in logarithms * Linearithmic * List of integrals of logarithmic functions * Logarithmic growth * Logarithmic timeline * Log-likelihood ratio * Log-log, Log-log graph * Log-normal distribution * Log-periodic antenna * Log-Weibull distribution * Logarithmic algorithm * Logarithmic convolution * Logarithmic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logarithm
In mathematics, the logarithm is the inverse function to exponentiation. That means the logarithm of a number to the base is the exponent to which must be raised, to produce . For example, since , the ''logarithm base'' 10 of is , or . The logarithm of to ''base'' is denoted as , or without parentheses, , or even without the explicit base, , when no confusion is possible, or when the base does not matter such as in big O notation. The logarithm base is called the decimal or common logarithm and is commonly used in science and engineering. The natural logarithm has the number as its base; its use is widespread in mathematics and physics, because of its very simple derivative. The binary logarithm uses base and is frequently used in computer science. Logarithms were introduced by John Napier in 1614 as a means of simplifying calculations. They were rapidly adopted by navigators, scientists, engineers, surveyors and others to perform high-a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
E (mathematical Constant)
The number , also known as Euler's number, is a mathematical constant approximately equal to 2.71828 that can be characterized in many ways. It is the base of the natural logarithms. It is the limit of as approaches infinity, an expression that arises in the study of compound interest. It can also be calculated as the sum of the infinite series e = \sum\limits_^ \frac = 1 + \frac + \frac + \frac + \cdots. It is also the unique positive number such that the graph of the function has a slope of 1 at . The (natural) exponential function is the unique function that equals its own derivative and satisfies the equation ; hence one can also define as . The natural logarithm, or logarithm to base , is the inverse function to the natural exponential function. The natural logarithm of a number can be defined directly as the area under the curve between and , in which case is the value of for which this area equals one (see image). There are various other characteriz ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logarithmic Timeline
A logarithmic timeline is a timeline laid out according to a logarithmic scale. This necessarily implies a zero point and an infinity point, neither of which can be displayed. The most natural zero point is the Big Bang, looking forward, but the most common is the ever-changing present, looking backward. (Also possible is a zero point in the present, looking forward to the infinite future.) The idea of presenting history logarithmically goes back at least to 1932, when John B. Sparks copyrighted his chart "Histomap of Evolution". Around the same time it was also explored by the cyberneticist Heinz von Foerster, who used it to propose that memories naturally fade in an exponential manner. Logarithmic timelines have also been used in futures studies to justify the idea of a technological singularity. A logarithmic scale enables events throughout time to be presented accurately, but enables more events to be included closer to one end. Sparks explained this by stating: : ''As we t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logarithmic Growth
In mathematics, logarithmic growth describes a phenomenon whose size or cost can be described as a logarithm function of some input. e.g. ''y'' = ''C'' log (''x''). Note that any logarithm base can be used, since one can be converted to another by multiplying by a fixed constant.. Logarithmic growth is the inverse of exponential growth and is very slow. A familiar example of logarithmic growth is a number, ''N'', in positional notation, which grows as log''b'' (''N''), where ''b'' is the base of the number system used, e.g. 10 for decimal arithmetic. In more advanced mathematics, the partial sums of the harmonic series :1+\frac+\frac+\frac+\frac+\cdots grow logarithmically. In the design of computer algorithms, logarithmic growth, and related variants, such as log-linear, or linearithmic, growth are very desirable indications of efficiency, and occur in the time complexity analysis of algorithms such as binary search. Logarithmic growth can lead to apparent pa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Integrals Of Logarithmic Functions
The following is a list of integrals (antiderivative functions) of logarithmic functions. For a complete list of integral functions, see list of integrals. ''Note:'' ''x'' > 0 is assumed throughout this article, and the constant of integration is omitted for simplicity. Integrals involving only logarithmic functions : \int\log_a x\,dx = x\log_a x - \frac = \frac : \int\ln(ax)\,dx = x\ln(ax) - x : \int\ln (ax + b)\,dx = \frac : \int (\ln x)^2\,dx = x(\ln x)^2 - 2x\ln x + 2x : \int (\ln x)^n\,dx = x\sum^_(-1)^ \frac(\ln x)^k : \int \frac = \ln, \ln x, + \ln x + \sum^\infty_\frac : \int \frac = \operatorname(x), the logarithmic integral. : \int \frac = -\frac + \frac\int\frac \qquad\mboxn\neq 1\mbox : \int \ln f(x)\,dx = x\ln f(x) - \int x\frac\,dx \qquad\mbox f(x) > 0\mbox Integrals involving logarithmic and power functions : \int x^m\ln x\,dx = x^\left(\frac-\frac\right) \qquad\mboxm\neq -1\mbox : \int x^m (\ln x)^n\,dx = \frac - \frac\int x^m (\ln x)^ dx \qquad\mbo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linearithmic
In computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations performed by the algorithm, supposing that each elementary operation takes a fixed amount of time to perform. Thus, the amount of time taken and the number of elementary operations performed by the algorithm are taken to be related by a constant factor. Since an algorithm's running time may vary among different inputs of the same size, one commonly considers the worst-case time complexity, which is the maximum amount of time required for inputs of a given size. Less common, and usually specified explicitly, is the average-case complexity, which is the average of the time taken on inputs of a given size (this makes sense because there are only a finite number of possible inputs of a given size). In both cases, the time complexity is generally expresse ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Form In Logarithms
In transcendental number theory, a mathematical discipline, Baker's theorem gives a lower bound for the absolute value of linear combinations of logarithms of algebraic numbers. The result, proved by , subsumed many earlier results in transcendental number theory and solved a problem posed by Alexander Gelfond nearly fifteen years earlier. Baker used this to prove the transcendence of many numbers, to derive effective bounds for the solutions of some Diophantine equations, and to solve the class number problem of finding all imaginary quadratic fields with class number 1. History To simplify notation, let \mathbb be the set of logarithms to the base ''e'' of nonzero algebraic numbers, that is \mathbb = \left \, where \Complex denotes the set of complex numbers and \overline denotes the algebraic numbers (the algebraic completion of the rational numbers \Q). Using this notation, several results in transcendental number theory become much easier to state. For example the Hermite–L ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
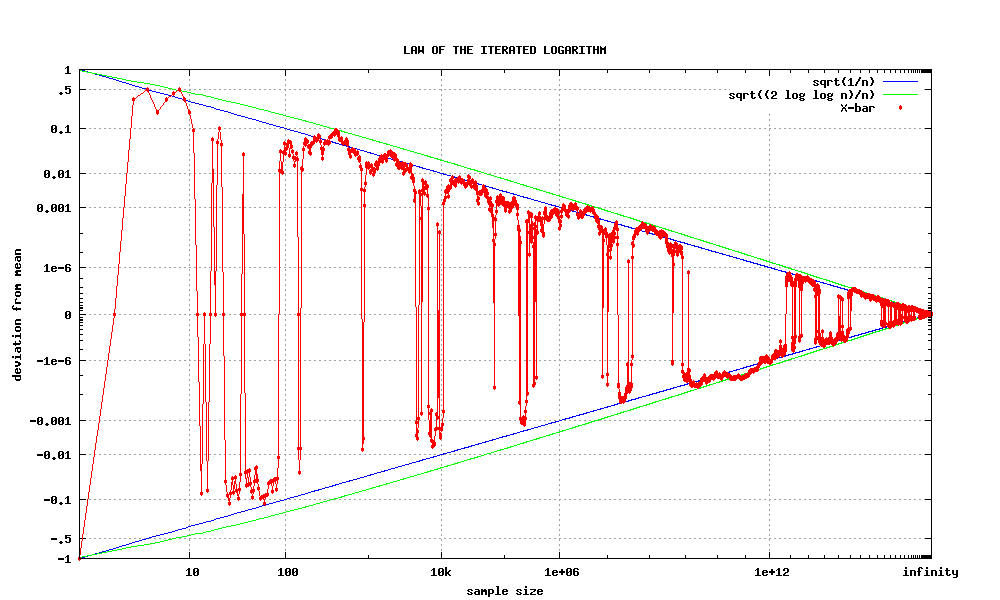
Law Of The Iterated Logarithm
In probability theory, the law of the iterated logarithm describes the magnitude of the fluctuations of a random walk. The original statement of the law of the iterated logarithm is due to A. Ya. Khinchin (1924). Another statement was given by A. N. Kolmogorov in 1929. Statement Let be independent, identically distributed random variables with means zero and unit variances. Let ''S''''n'' = ''Y''1 + ... + ''Y''''n''. Then : \limsup_ \frac = 1 \quad \text, where “log” is the natural logarithm, “lim sup” denotes the limit superior, and “a.s.” stands for “almost surely”. Discussion The law of iterated logarithms operates “in between” the law of large numbers and the central limit theorem. There are two versions of the law of large numbers — the weak and the strong — and they both state that the sums ''S''''n'', scaled by ''n''−1, converge to zero, respectively in probability and almost surely: : \frac \ \xrightarrow\ 0, \qquad \frac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Otis King
Otis Carter Formby King (1876–1944) was an electrical engineer in London who invented and produced a cylindrical slide rule with helical scales, primarily for business uses initially. The product was named Otis King's Patent Calculator, and was manufactured and sold by Carbic Ltd. in London from about 1922 to about 1972. With a log-scale decade length of 66 inches, the Otis King calculator should be about a full digit more accurate than a 6-inch pocket slide rule. But due to inaccuracies in tic-mark placement, some portions of its scales will read off by more than they should. For example, a reading of 4.630 might represent an answer of 4.632, or almost one part in 2000 error, when it should be accurate to one part in 6000 (66"/6000 = 0.011" estimated interpolation accuracy). The Geniac brand cylindrical slide rule sold by Oliver Garfield Company in New York was initially a relabelled Otis King; Garfield later made his own, probably unauthorized version of the Otis King ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Iterated Logarithm
In computer science, the iterated logarithm of n, written n (usually read "log star"), is the number of times the logarithm function must be iteratively applied before the result is less than or equal to 1. The simplest formal definition is the result of this recurrence relation: : \log^* n := \begin 0 & \mbox n \le 1; \\ 1 + \log^*(\log n) & \mbox n > 1 \end On the positive real numbers, the continuous super-logarithm (inverse tetration) is essentially equivalent: :\log^* n = \lceil \mathrm _e(n) \rceil i.e. the base ''b'' iterated logarithm is \log^* n = y if n lies within the interval ^b on the ''x''-axis. In computer science, is often used to indicate the binary iterated logarithm, which iterates the binary logarithm (with base 2) instead of the natural logarithm (with base ''e''). Mathematically, the iterated logarithm is well-defined for any base greater than e^ \approx 1.444667, not only for base 2 and base ''e''. Analysis of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Sector
A hyperbolic sector is a region of the Cartesian plane bounded by a hyperbola and two rays from the origin to it. For example, the two points and on the rectangular hyperbola , or the corresponding region when this hyperbola is re-scaled and its orientation is altered by a rotation leaving the center at the origin, as with the unit hyperbola. A hyperbolic sector in standard position has and . Hyperbolic sectors are the basis for the hyperbolic functions. Area The area of a hyperbolic sector in standard position is natural logarithm of ''b'' . Proof: Integrate under 1/''x'' from 1 to ''b'', add triangle , and subtract triangle . When in standard position, a hyperbolic sector corresponds to a positive hyperbolic angle at the origin, with the measure of the latter being defined as the area of the former. Hyperbolic triangle When in standard position, a hyperbolic sector determines a hyperbolic triangle, the right triangle with one vertex at the origin, base on the diag ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
History Of Logarithms
The history of logarithms is the story of a correspondence (in modern terms, a group isomorphism) between multiplication on the positive real numbers and addition on the real number line that was formalized in seventeenth century Europe and was widely used to simplify calculation until the advent of the digital computer. The Napierian logarithms were published first in 1614. E. W. Hobson called it "one of the very greatest scientific discoveries that the world has seen." Henry Briggs introduced common (base 10) logarithms, which were easier to use. Tables of logarithms were published in many forms over four centuries. The idea of logarithms was also used to construct the slide rule, which became ubiquitous in science and engineering until the 1970s. A breakthrough generating the natural logarithm was the result of a search for an expression of area against a rectangular hyperbola, and required the assimilation of a new function into standard mathematics. Napier's wonderful inve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
