|
Linear Recurrence With Constant Coefficients
In mathematics (including combinatorics, linear algebra, and dynamical systems), a linear recurrence with constant coefficients (also known as a linear recurrence relation or linear difference equation) sets equal to 0 a polynomial that is linear in the various iterates of a variable—that is, in the values of the elements of a sequence. The polynomial's linearity means that each of its terms has degree 0 or 1. A linear recurrence denotes the evolution of some variable over time, with the current time period or discrete moment in time denoted as , one period earlier denoted as , one period later as , etc. The ''solution'' of such an equation is a function of , and not of any iterate values, giving the value of the iterate at any time. To find the solution it is necessary to know the specific values (known as ''initial conditions'') of of the iterates, and normally these are the iterates that are oldest. The equation or its variable is said to be ''stable'' if from any set of ini ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time Series
In mathematics, a time series is a series of data points indexed (or listed or graphed) in time order. Most commonly, a time series is a sequence taken at successive equally spaced points in time. Thus it is a sequence of discrete-time data. Examples of time series are heights of ocean tides, counts of sunspots, and the daily closing value of the Dow Jones Industrial Average. A time series is very frequently plotted via a run chart (which is a temporal line chart). Time series are used in statistics, signal processing, pattern recognition, econometrics, mathematical finance, weather forecasting, earthquake prediction, electroencephalography, control engineering, astronomy, communications engineering, and largely in any domain of applied science and engineering which involves temporal measurements. Time series ''analysis'' comprises methods for analyzing time series data in order to extract meaningful statistics and other characteristics of the data. Time series ''forecasting' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
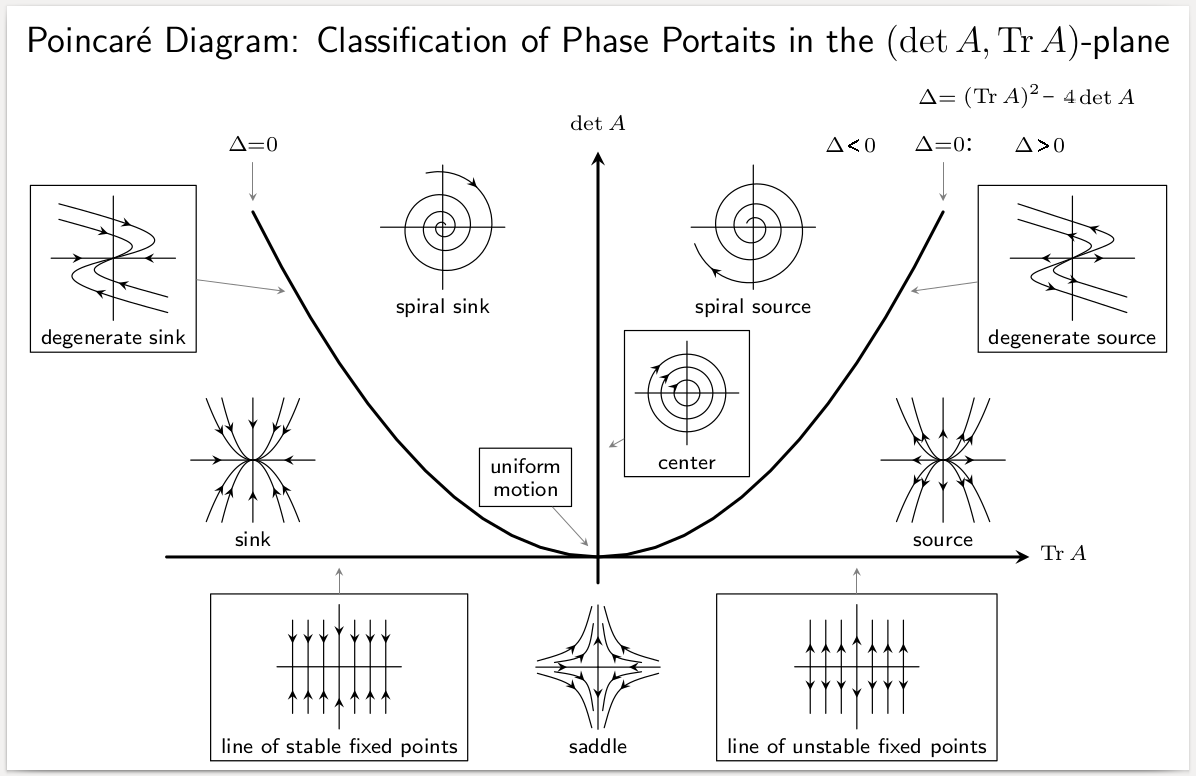
Stability Theory
In mathematics, stability theory addresses the stability of solutions of differential equations and of trajectories of dynamical systems under small perturbations of initial conditions. The heat equation, for example, is a stable partial differential equation because small perturbations of initial data lead to small variations in temperature at a later time as a result of the maximum principle. In partial differential equations one may measure the distances between functions using Lp norms or the sup norm, while in differential geometry one may measure the distance between spaces using the Gromov–Hausdorff distance. In dynamical systems, an orbit is called ''Lyapunov stable'' if the forward orbit of any point is in a small enough neighborhood or it stays in a small (but perhaps, larger) neighborhood. Various criteria have been developed to prove stability or instability of an orbit. Under favorable circumstances, the question may be reduced to a well-studied problem involvi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Characteristic Root
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted by \lambda, is the factor by which the eigenvector is scaled. Geometrically, an eigenvector, corresponding to a real nonzero eigenvalue, points in a direction in which it is stretched by the transformation and the eigenvalue is the factor by which it is stretched. If the eigenvalue is negative, the direction is reversed. Loosely speaking, in a multidimensional vector space, the eigenvector is not rotated. Formal definition If is a linear transformation from a vector space over a field into itself and is a nonzero vector in , then is an eigenvector of if is a scalar multiple of . This can be written as T(\mathbf) = \lambda \mathbf, where is a scalar in , known as the eigenvalue, characteristic value, or characteristic root ass ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ansatz
In physics and mathematics, an ansatz (; , meaning: "initial placement of a tool at a work piece", plural Ansätze ; ) is an educated guess or an additional assumption made to help solve a problem, and which may later be verified to be part of the solution by its results. Use An ansatz is the establishment of the starting equation(s), the theorem(s), or the value(s) describing a mathematical or physical problem or solution. It typically provides an initial estimate or framework to the solution of a mathematical problem, and can also take into consideration the boundary conditions (in fact, an ansatz is sometimes thought of as a "trial answer" and an important technique in solving differential equations). After an ansatz, which constitutes nothing more than an assumption, has been established, the equations are solved more precisely for the general function of interest, which then constitutes a confirmation of the assumption. In essence, an ansatz makes assumptions about the form o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Formal Power Series
In mathematics, a formal series is an infinite sum that is considered independently from any notion of convergence, and can be manipulated with the usual algebraic operations on series (addition, subtraction, multiplication, division, partial sums, etc.). A formal power series is a special kind of formal series, whose terms are of the form a x^n where x^n is the nth power of a variable x (n is a non-negative integer), and a is called the coefficient. Hence, power series can be viewed as a generalization of polynomials, where the number of terms is allowed to be infinite, with no requirements of convergence. Thus, the series may no longer represent a function of its variable, merely a formal sequence of coefficients, in contrast to a power series, which defines a function by taking numerical values for the variable within a radius of convergence. In a formal power series, the x^n are used only as position-holders for the coefficients, so that the coefficient of x^5 is the fifth ter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generating Function
In mathematics, a generating function is a way of encoding an infinite sequence of numbers () by treating them as the coefficients of a formal power series. This series is called the generating function of the sequence. Unlike an ordinary series, the ''formal'' power series is not required to converge: in fact, the generating function is not actually regarded as a function, and the "variable" remains an indeterminate. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general linear recurrence problem. One can generalize to formal power series in more than one indeterminate, to encode information about infinite multi-dimensional arrays of numbers. There are various types of generating functions, including ordinary generating functions, exponential generating functions, Lambert series, Bell series, and Dirichlet series; definitions and examples are given below. Every sequence in principle has a generating function of each type (except ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Characteristic Polynomial
In linear algebra, the characteristic polynomial of a square matrix is a polynomial which is invariant under matrix similarity and has the eigenvalues as roots. It has the determinant and the trace of the matrix among its coefficients. The characteristic polynomial of an endomorphism of a finite-dimensional vector space is the characteristic polynomial of the matrix of that endomorphism over any base (that is, the characteristic polynomial does not depend on the choice of a basis). The characteristic equation, also known as the determinantal equation, is the equation obtained by equating the characteristic polynomial to zero. In spectral graph theory, the characteristic polynomial of a graph is the characteristic polynomial of its adjacency matrix. Motivation In linear algebra, eigenvalues and eigenvectors play a fundamental role, since, given a linear transformation, an eigenvector is a vector whose direction is not changed by the transformation, and the corresponding eigenva ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Characteristic Polynomial
In linear algebra, the characteristic polynomial of a square matrix is a polynomial which is invariant under matrix similarity and has the eigenvalues as roots. It has the determinant and the trace of the matrix among its coefficients. The characteristic polynomial of an endomorphism of a finite-dimensional vector space is the characteristic polynomial of the matrix of that endomorphism over any base (that is, the characteristic polynomial does not depend on the choice of a basis). The characteristic equation, also known as the determinantal equation, is the equation obtained by equating the characteristic polynomial to zero. In spectral graph theory, the characteristic polynomial of a graph is the characteristic polynomial of its adjacency matrix. Motivation In linear algebra, eigenvalues and eigenvectors play a fundamental role, since, given a linear transformation, an eigenvector is a vector whose direction is not changed by the transformation, and the corresponding eigenva ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parameter
A parameter (), generally, is any characteristic that can help in defining or classifying a particular system (meaning an event, project, object, situation, etc.). That is, a parameter is an element of a system that is useful, or critical, when identifying the system, or when evaluating its performance, status, condition, etc. ''Parameter'' has more specific meanings within various disciplines, including mathematics, computer programming, engineering, statistics, logic, linguistics, and electronic musical composition. In addition to its technical uses, there are also extended uses, especially in non-scientific contexts, where it is used to mean defining characteristics or boundaries, as in the phrases 'test parameters' or 'game play parameters'. Modelization When a system is modeled by equations, the values that describe the system are called ''parameters''. For example, in mechanics, the masses, the dimensions and shapes (for solid bodies), the densities and the viscosities ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Autoregressive Moving Average
In statistics, econometrics and signal processing, an autoregressive (AR) model is a representation of a type of random process; as such, it is used to describe certain time-varying processes in nature, economics, etc. The autoregressive model specifies that the output variable depends linearly on its own previous values and on a stochastic term (an imperfectly predictable term); thus the model is in the form of a stochastic difference equation (or recurrence relation which should not be confused with differential equation). Together with the moving-average (MA) model, it is a special case and key component of the more general autoregressive–moving-average (ARMA) and autoregressive integrated moving average (ARIMA) models of time series, which have a more complicated stochastic structure; it is also a special case of the vector autoregressive model (VAR), which consists of a system of more than one interlocking stochastic difference equation in more than one evolving random vari ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector Autoregression
Vector autoregression (VAR) is a statistical model used to capture the relationship between multiple quantities as they change over time. VAR is a type of stochastic process model. VAR models generalize the single-variable (univariate) autoregressive model by allowing for multivariate time series. VAR models are often used in economics and the natural sciences. Like the autoregressive model, each variable has an equation modelling its evolution over time. This equation includes the variable's lagged (past) values, the lagged values of the other variables in the model, and an error term. VAR models do not require as much knowledge about the forces influencing a variable as do structural models with simultaneous equations. The only prior knowledge required is a list of variables which can be hypothesized to affect each other over time. Specification Definition A VAR model describes the evolution of a set of ''k'' variables, called ''endogenous variables'', over time. Each perio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
