|
Line Of Application
In physics, the line of action (also called line of application) of a force ''(F)'' is a geometric representation of how the force is applied. It is the line through the point at which the force is applied in the same direction as the vector .Mungan, Carl E. "Acceleration of a pulled spool." The Physics Teacher 39.8 (2001): 481-485. https://www.usna.edu/Users/physics/mungan/_files/documents/Publications/TPT.pdf The concept is essential, for instance, for understanding the net effect of multiple forces applied to a body. For example, if two forces of equal magnitude act upon a rigid body along the same line of action but in opposite directions, they cancel and have no net effect. But if, instead, their lines of action are not identical, but merely parallel, then their effect is to create a moment on the body, which tends to rotate it. Calculation of torque For the simple geometry associated with the figure, there are three equivalent equations for the magnitude of the torqu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Torque Lever Arm W Point Of Application And Line Of Action
In physics and mechanics, torque is the rotational equivalent of linear force. It is also referred to as the moment of force (also abbreviated to moment). It represents the capability of a force to produce change in the rotational motion of the body. The concept originated with the studies by Archimedes of the usage of levers, which is reflected in his famous quote: "''Give me a lever and a place to stand and I will move the Earth''". Just as a linear force is a push or a pull, a torque can be thought of as a twist to an object around a specific axis. Torque is defined as the product of the magnitude of the perpendicular component of the force and the distance of the line of action of a force from the point around which it is being determined. The law of conservation of energy can also be used to understand torque. The symbol for torque is typically \boldsymbol\tau, the lowercase Greek letter ''tau''. When being referred to as moment of force, it is commonly denoted by . In ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." Physics is one of the most fundamental scientific disciplines, with its main goal being to understand how the universe behaves. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Force
In physics, a force is an influence that can change the motion of an object. A force can cause an object with mass to change its velocity (e.g. moving from a state of rest), i.e., to accelerate. Force can also be described intuitively as a push or a pull. A force has both magnitude and direction, making it a vector quantity. It is measured in the SI unit of newton (N). Force is represented by the symbol (formerly ). The original form of Newton's second law states that the net force acting upon an object is equal to the rate at which its momentum changes with time. If the mass of the object is constant, this law implies that the acceleration of an object is directly proportional to the net force acting on the object, is in the direction of the net force, and is inversely proportional to the mass of the object. Concepts related to force include: thrust, which increases the velocity of an object; drag, which decreases the velocity of an object; and torque, which produce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Line (mathematics)
In geometry, a line is an infinitely long object with no width, depth, or curvature. Thus, lines are one-dimensional objects, though they may exist in two, three, or higher dimension spaces. The word ''line'' may also refer to a line segment in everyday life, which has two points to denote its ends. Lines can be referred by two points that lay on it (e.g., \overleftrightarrow) or by a single letter (e.g., \ell). Euclid described a line as "breadthless length" which "lies evenly with respect to the points on itself"; he introduced several postulates as basic unprovable properties from which he constructed all of geometry, which is now called Euclidean geometry to avoid confusion with other geometries which have been introduced since the end of the 19th century (such as non-Euclidean, projective and affine geometry). In modern mathematics, given the multitude of geometries, the concept of a line is closely tied to the way the geometry is described. For instance, in analytic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector (mathematics And Physics)
In mathematics and physics, vector is a term that refers colloquially to some quantities that cannot be expressed by a single number (a scalar), or to elements of some vector spaces. Historically, vectors were introduced in geometry and physics (typically in mechanics) for quantities that have both a magnitude and a direction, such as displacements, forces and velocity. Such quantities are represented by geometric vectors in the same way as distances, masses and time are represented by real numbers. The term ''vector'' is also used, in some contexts, for tuples, which are finite sequences of numbers of a fixed length. Both geometric vectors and tuples can be added and scaled, and these vector operations led to the concept of a vector space, which is a set equipped with a vector addition and a scalar multiplication that satisfy some axioms generalizing the main properties of operations on the above sorts of vectors. A vector space formed by geometric vectors is called a Euclidean ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Net Force , a young adult novel series
{{disambiguation ...
Net Force may refer to: * Net force, the overall force acting on an object * ''NetForce'' (film), a 1999 American television film * Tom Clancy's Net Force, a novel series * Tom Clancy's Net Force Explorers Tom Clancy's Net Force Explorers or Net Force Explorers is a series of young adult fiction, young adult novels created by Tom Clancy and Steve Pieczenik as a spin-off of the military fiction series Tom Clancy's Net Force. The first novel was pub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physical Object
In common usage and classical mechanics, a physical object or physical body (or simply an object or body) is a collection of matter within a defined contiguous boundary in three-dimensional space. The boundary must be defined and identified by the properties of the material. The boundary may change over time. The boundary is usually the visible or tangible surface of the object. The matter in the object is constrained (to a greater or lesser degree) to move as one object. The boundary may move in space relative to other objects that it is not attached to (through translation and rotation). An object's boundary may also deform and change over time in other ways. Also in common usage, an object is not constrained to consist of the same collection of matter. Atoms or parts of an object may change over time. An object usually meant to be defined by the simplest representation of the boundary consistent with the observations. However the laws of physics only apply directly to objects ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Magnitude (mathematics)
In mathematics, the magnitude or size of a mathematical object is a property which determines whether the object is larger or smaller than other objects of the same kind. More formally, an object's magnitude is the displayed result of an order theory, ordering (or ranking)—of the class (mathematics), class of objects to which it belongs. In physics, magnitude can be defined as quantity or distance. History The Greeks distinguished between several types of magnitude, including: *Positive fractions *Line segments (ordered by length) *Geometric shape, Plane figures (ordered by area) *Solid geometry, Solids (ordered by volume) *Angle, Angles (ordered by angular magnitude) They proved that the first two could not be the same, or even isomorphic systems of magnitude. They did not consider negative number, negative magnitudes to be meaningful, and ''magnitude'' is still primarily used in contexts in which zero is either the smallest size or less than all possible sizes. Numbers Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Structural Rigidity
In discrete geometry and mechanics, structural rigidity is a combinatorial theory for predicting the flexibility of ensembles formed by rigid bodies connected by flexible linkages or hinges. Definitions Rigidity is the property of a structure that it does not bend or flex under an applied force. The opposite of rigidity is flexibility. In structural rigidity theory, structures are formed by collections of objects that are themselves rigid bodies, often assumed to take simple geometric forms such as straight rods (line segments), with pairs of objects connected by flexible hinges. A structure is rigid if it cannot flex; that is, if there is no continuous motion of the structure that preserves the shape of its rigid components and the pattern of their connections at the hinges. There are two essentially different kinds of rigidity. Finite or macroscopic rigidity means that the structure will not flex, fold, or bend by a positive amount. Infinitesimal rigidity means that the st ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallel (geometry)
In geometry, parallel lines are coplanar straight lines that do not intersect at any point. Parallel planes are planes in the same three-dimensional space that never meet. ''Parallel curves'' are curves that do not touch each other or intersect and keep a fixed minimum distance. In three-dimensional Euclidean space, a line and a plane that do not share a point are also said to be parallel. However, two noncoplanar lines are called ''skew lines''. Parallel lines are the subject of Euclid's parallel postulate. Parallelism is primarily a property of affine geometries and Euclidean geometry is a special instance of this type of geometry. In some other geometries, such as hyperbolic geometry, lines can have analogous properties that are referred to as parallelism. Symbol The parallel symbol is \parallel. For example, AB \parallel CD indicates that line ''AB'' is parallel to line ''CD''. In the Unicode character set, the "parallel" and "not parallel" signs have codepoint ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
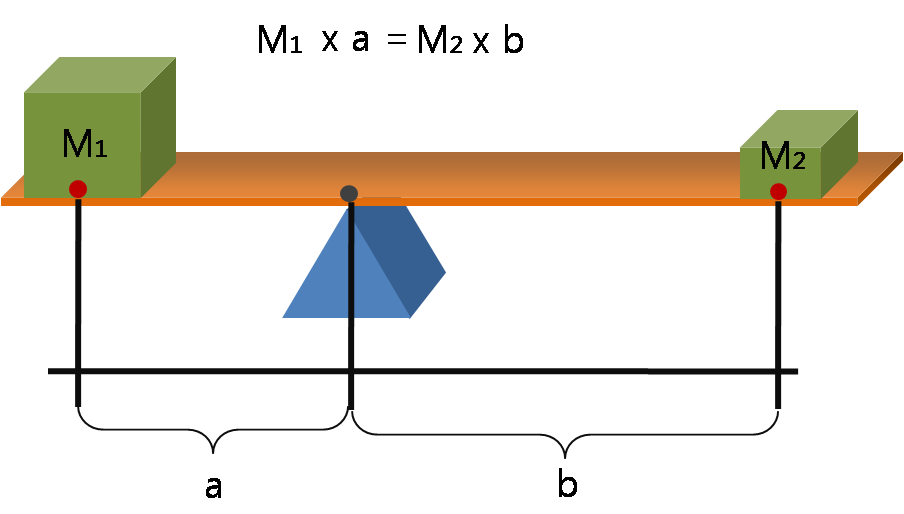
Moment (physics)
In physics, a moment is a mathematical expression involving the product of a distance and physical quantity. Moments are usually defined with respect to a fixed reference point and refer to physical quantities located some distance from the reference point. In this way, the moment accounts for the quantity's location or arrangement. For example, the moment of force, often called torque, is the product of a force on an object and the distance from the reference point to the object. In principle, any physical quantity can be multiplied by a distance to produce a moment. Commonly used quantities include forces, masses, and electric charge distributions. Elaboration In its most basic form, a moment is the product of the distance to a point, raised to a power, and a physical quantity (such as force or electrical charge) at that point: : \mu_n = r^n\,Q, where Q is the physical quantity such as a force applied at a point, or a point charge, or a point mass, etc. If the quantity ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rotation Around A Fixed Axis
Rotation around a fixed axis is a special case of rotational motion. The fixed-axis hypothesis excludes the possibility of an axis changing its orientation and cannot describe such phenomena as wobbling or precession. According to Euler's rotation theorem, simultaneous rotation along a number of stationary axes at the same time is impossible; if two rotations are forced at the same time, a new axis of rotation will appear. This article assumes that the rotation is also stable, such that no torque is required to keep it going. The kinematics and dynamics of rotation around a fixed axis of a rigid body are mathematically much simpler than those for free rotation of a rigid body; they are entirely analogous to those of linear motion along a single fixed direction, which is not true for ''free rotation of a rigid body''. The expressions for the kinetic energy of the object, and for the forces on the parts of the object, are also simpler for rotation around a fixed axis, than for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.png "Click for more on -> Parallel (geometry)")
