|
Levenshtein Distance
In information theory, linguistics, and computer science, the Levenshtein distance is a string metric for measuring the difference between two sequences. The Levenshtein distance between two words is the minimum number of single-character edits (insertions, deletions or substitutions) required to change one word into the other. It is named after Soviet mathematician Vladimir Levenshtein, who defined the metric in 1965. Levenshtein distance may also be referred to as ''edit distance'', although that term may also denote a larger family of distance metrics known collectively as edit distance. It is closely related to pairwise string alignments. Definition The Levenshtein distance between two strings a, b (of length , a, and , b, respectively) is given by \operatorname(a, b) where : \operatorname(a, b) = \begin , a, & \text , b, = 0, \\ , b, & \text , a, = 0, \\ \operatorname\big(\operatorname(a),\operatorname(b)\big) & \text \operatorname(a)= \operatorname(b), \\ 1 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Information Theory
Information theory is the mathematical study of the quantification (science), quantification, Data storage, storage, and telecommunications, communication of information. The field was established and formalized by Claude Shannon in the 1940s, though early contributions were made in the 1920s through the works of Harry Nyquist and Ralph Hartley. It is at the intersection of electronic engineering, mathematics, statistics, computer science, Neuroscience, neurobiology, physics, and electrical engineering. A key measure in information theory is information entropy, entropy. Entropy quantifies the amount of uncertainty involved in the value of a random variable or the outcome of a random process. For example, identifying the outcome of a Fair coin, fair coin flip (which has two equally likely outcomes) provides less information (lower entropy, less uncertainty) than identifying the outcome from a roll of a dice, die (which has six equally likely outcomes). Some other important measu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Record Linkage
Record linkage (also known as data matching, data linkage, entity resolution, and many other terms) is the task of finding records in a data set that refer to the same entity across different data sources (e.g., data files, books, websites, and databases). Record linkage is necessary when joining different data sets based on entities that may or may not share a common identifier (e.g., database key, URI, National identification number), which may be due to differences in record shape, storage location, or curator style or preference. A data set that has undergone RL-oriented reconciliation may be referred to as being ''cross-linked''. Naming conventions "Record linkage" is the term used by statisticians, epidemiologists, and historians, among others, to describe the process of joining records from one data source with another that describe the same entity. However, many other terms are used for this process. Unfortunately, this profusion of terminology has led to few cross- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prefix (computer Science)
In formal language theory and computer science, a substring is a contiguous sequence of characters within a string. For instance, "''the best of''" is a substring of "''It was the best of times''". In contrast, "''Itwastimes''" is a subsequence of "''It was the best of times''", but not a substring. Prefixes and suffixes are special cases of substrings. A prefix of a string S is a substring of S that occurs at the beginning of S; likewise, a suffix of a string S is a substring that occurs at the end of S. The substrings of the string "''apple''" would be: "''a''", "''ap''", "''app''", "''appl''", "''apple''", "''p''", "''pp''", "''ppl''", "''pple''", "''pl''", "''ple''", "''l''", "''le''" "''e''", "" (note the empty string at the end). Substring A string u is a substring (or factor) of a string t if there exists two strings p and s such that t = pus. In particular, the empty string is a substring of every string. Example: The string u=ana is equal to substrings (and sub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix (mathematics)
In mathematics, a matrix (: matrices) is a rectangle, rectangular array or table of numbers, symbol (formal), symbols, or expression (mathematics), expressions, with elements or entries arranged in rows and columns, which is used to represent a mathematical object or property of such an object. For example, \begin1 & 9 & -13 \\20 & 5 & -6 \end is a matrix with two rows and three columns. This is often referred to as a "two-by-three matrix", a " matrix", or a matrix of dimension . Matrices are commonly used in linear algebra, where they represent linear maps. In geometry, matrices are widely used for specifying and representing geometric transformations (for example rotation (mathematics), rotations) and coordinate changes. In numerical analysis, many computational problems are solved by reducing them to a matrix computation, and this often involves computing with matrices of huge dimensions. Matrices are used in most areas of mathematics and scientific fields, either directly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Haskell (programming Language)
Haskell () is a General-purpose programming language, general-purpose, static typing, statically typed, purely functional programming, purely functional programming language with type inference and lazy evaluation. Designed for teaching, research, and industrial applications, Haskell pioneered several programming language #Features, features such as type classes, which enable type safety, type-safe operator overloading, and Monad (functional programming), monadic input/output (IO). It is named after logician Haskell Curry. Haskell's main implementation is the Glasgow Haskell Compiler (GHC). Haskell's Semantics (computer science), semantics are historically based on those of the Miranda (programming language), Miranda programming language, which served to focus the efforts of the initial Haskell working group. The last formal specification of the language was made in July 2010, while the development of GHC continues to expand Haskell via language extensions. Haskell is used in a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
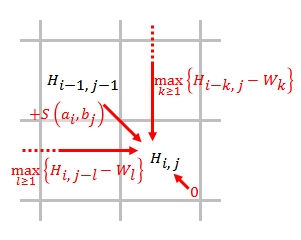
Smith–Waterman Algorithm
The Smith–Waterman algorithm performs local sequence alignment; that is, for determining similar regions between two strings of nucleic acid sequences or protein sequences. Instead of looking at the entire sequence, the Smith–Waterman algorithm compares segments of all possible lengths and optimizes the similarity measure. The algorithm was first proposed by Temple F. Smith and Michael S. Waterman in 1981. Like the Needleman–Wunsch algorithm, of which it is a variation, Smith–Waterman is a dynamic programming algorithm. As such, it has the desirable property that it is guaranteed to find the optimal local alignment with respect to the scoring system being used (which includes the substitution matrix and the gap-scoring scheme). The main difference to the Needleman–Wunsch algorithm is that negative scoring matrix cells are set to zero. Traceback procedure starts at the highest scoring matrix cell and proceeds until a cell with score zero is encountered, yielding the h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sequence Alignment
In bioinformatics, a sequence alignment is a way of arranging the sequences of DNA, RNA, or protein to identify regions of similarity that may be a consequence of functional, structural biology, structural, or evolutionary relationships between the sequences. Aligned sequences of nucleotide or amino acid residues are typically represented as rows within a matrix (mathematics), matrix. Gaps are inserted between the Residue (chemistry), residues so that identical or similar characters are aligned in successive columns. Sequence alignments are also used for non-biological sequences such as calculating the Edit distance, distance cost between strings in a natural language, or to display financial data. Interpretation If two sequences in an alignment share a common ancestor, mismatches can be interpreted as point mutations and gaps as indels (that is, insertion or deletion mutations) introduced in one or both lineages in the time since they diverged from one another. In sequence ali ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Edit Distance
In computational linguistics and computer science, edit distance is a string metric, i.e. a way of quantifying how dissimilar two String (computing), strings (e.g., words) are to one another, that is measured by counting the minimum number of operations required to transform one string into the other. Edit distances find applications in natural language processing, where automatic Spell checker, spelling correction can determine candidate corrections for a misspelled word by selecting words from a dictionary that have a low distance to the word in question. In bioinformatics, it can be used to quantify the similarity of DNA sequences, which can be viewed as strings of the letters A, C, G and T. Different definitions of an edit distance use different sets of like operations. Levenshtein distance operations are the removal, insertion, or substitution of a character in the string. Being the most common metric, the term ''Levenshtein distance'' is often used interchangeably with ''edit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jaro Distance
{{disambig, geo ...
Jaro may refer to: *Jaro, Iloilo City, a district of Iloilo City, Philippines *Jaro, Indonesia, a subdistrict in Tabalong Regency, South Kalimantan *Jaro, Leyte, a municipality in the province of Leyte, Philippines *Jaro Medien (Jaro Media), a German music company *JARO Records, an American subsidiary of Rank Records Ltd (UK) *Jaro–Winkler distance *FF Jaro, a Finnish football club * Jaro, a character in the book ''The Letter for the King'' *Killamanjaro, nicknamed Jaro, a Reggae sound system See also Other places with a similar pronunciation or spelling: * Haro * Jarrow Jarrow ( or ) is a town in South Tyneside in the county of Tyne and Wear, England. Historically in County Durham, it is on the south bank of the River Tyne, about from the east coast. The 2011 census area classed Hebburn and the Boldons as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Longest Common Subsequence Problem
A longest common subsequence (LCS) is the longest subsequence common to all sequences in a set of sequences (often just two sequences). It differs from the longest common substring: unlike substrings, subsequences are not required to occupy consecutive positions within the original sequences. The problem of computing longest common subsequences is a classic computer science problem, the basis of data comparison programs such as the diff utility, and has applications in computational linguistics and bioinformatics. It is also widely used by revision control systems such as Git for reconciling multiple changes made to a revision-controlled collection of files. For example, consider the sequences (ABCD) and (ACBAD). They have five length-2 common subsequences: (AB), (AC), (AD), (BD), and (CD); two length-3 common subsequences: (ABD) and (ACD); and no longer common subsequences. So (ABD) and (ACD) are their longest common subsequences. Complexity For the general case of an ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transposition (mathematics)
In mathematics, and in particular in group theory, a cyclic permutation is a permutation consisting of a single cycle. In some cases, cyclic permutations are referred to as cycles; if a cyclic permutation has ''k'' elements, it may be called a ''k''-cycle. Some authors widen this definition to include permutations with fixed points in addition to at most one non-trivial cycle. In Permutation#Cycle notation, cycle notation, cyclic permutations are denoted by the list of their elements enclosed with parentheses, in the order to which they are permuted. For example, the permutation (1 3 2 4) that sends 1 to 3, 3 to 2, 2 to 4 and 4 to 1 is a 4-cycle, and the permutation (1 3 2)(4) that sends 1 to 3, 3 to 2, 2 to 1 and 4 to 4 is considered a 3-cycle by some authors. On the other hand, the permutation (1 3)(2 4) that sends 1 to 3, 3 to 1, 2 to 4 and 4 to 2 is not a cyclic permutation because it separately permutes the pairs and . For the wider definition of a cyclic permutation, allowi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |