|
Leonardo Number
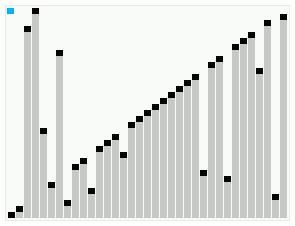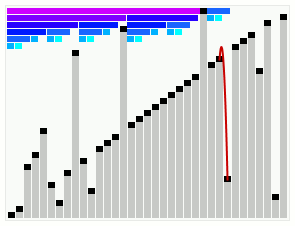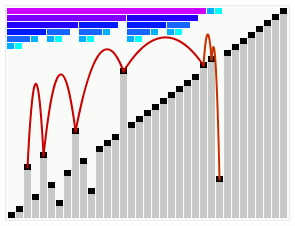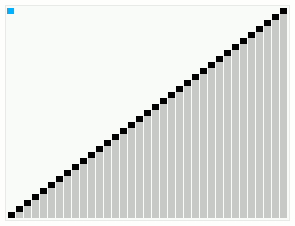
The Leonardo numbers are a sequence of numbers given by the recurrence: : L(n) = \begin 1 & \mbox n = 0 \\ 1 & \mbox n = 1 \\ L(n - 1) + L(n - 2) + 1 & \mbox n > 1 \\ \end Edsger W. Dijkstra used them as an integral part of his smoothsort algorithm, and also analyzed them in some detail. A Leonardo prime is a Leonardo number that's also prime. Values The first few Leonardo numbers are :1, 1, 3, 5, 9, 15, 25, 41, 67, 109, 177, 287, 465, 753, 1219, 1973, 3193, 5167, 8361, ... The first few Leonardo primes are : 3, 5, 41, 67, 109, 1973, 5167, 2692537, 11405773, 126491971, 331160281, 535828591, 279167724889, 145446920496281, 28944668049352441, 5760134388741632239, 63880869269980199809, 167242286979696845953, 597222253637954133837103, ... Modulo cycles The Leonardo numbers form a cycle in any modulo n≥2. An easy way to see it is: * If a pair of numbers modulo n appears twice in the sequence, then there's a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Smoothsort
In computer science, smoothsort is a comparison-based sorting algorithm. A variant of heapsort, it was invented and published by Edsger Dijkstra in 1981. Like heapsort, smoothsort is an in-place algorithm with an upper bound of , but it is not a stable sort. The advantage of smoothsort is that it comes closer to time if the input is already sorted to some degree, whereas heapsort averages regardless of the initial sorted state. Overview Like heapsort, smoothsort organizes the input into a priority queue and then repeatedly extracts the maximum. Also like heapsort, the priority queue is an implicit heap data structure (a heap-ordered implicit binary tree), which occupies a prefix of the array. Each extraction shrinks the prefix and adds the extracted element to a growing sorted suffix. When the prefix has shrunk to nothing, the array is completely sorted. Heapsort maps the binary tree to the array using a top-down breadth-first traversal of the tree; the array begins with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algorithm
In mathematics and computer science, an algorithm () is a finite sequence of rigorous instructions, typically used to solve a class of specific Computational problem, problems or to perform a computation. Algorithms are used as specifications for performing calculations and data processing. More advanced algorithms can perform automated deductions (referred to as automated reasoning) and use mathematical and logical tests to divert the code execution through various routes (referred to as automated decision-making). Using human characteristics as descriptors of machines in metaphorical ways was already practiced by Alan Turing with terms such as "memory", "search" and "stimulus". In contrast, a Heuristic (computer science), heuristic is an approach to problem solving that may not be fully specified or may not guarantee correct or optimal results, especially in problem domains where there is no well-defined correct or optimal result. As an effective method, an algorithm ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime Number
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, or , involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorized as a product of primes that is unique up to their order. The property of being prime is called primality. A simple but slow method of checking the primality of a given number n, called trial division, tests whether n is a multiple of any integer between 2 and \sqrt. Faster algorithms include the Miller–Rabin primality test, which is fast but has a small chance of error, and the AKS primality test, which always pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
41 (number)
41 (forty-one, XLI) is the natural number following 40 and preceding 42. In mathematics * the 13th smallest prime number. The next is 43, making both twin primes. * the sum of the first six prime numbers (2 + 3 + 5 + 7 + 11 + 13). * the 12th supersingular prime * a Newman–Shanks–Williams prime. * the smallest Sophie Germain prime to start a Cunningham chain of the first kind of three terms, . * an Eisenstein prime, with no imaginary part and real part of the form 3''n'' − 1. * a Proth prime as it is 5 × 23 + 1. * the largest lucky number of Euler: the polynomial yields primes for all the integers ''k'' with . * the sum of two squares, 42 + 52. * the sum of the sum of the divisors of the first 7 positive integers. * the smallest integer whose reciprocal has a 5-digit repetend. That is a consequence of the fact that 41 is a factor of 99999. * the smallest integer whose s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
67 (number)
67 (sixty-seven) is the natural number following 66 (number), 66 and preceding 68 (number), 68. It is an Parity (mathematics), odd number. In mathematics 67 is: *the 19th prime number (the next is 71 (number), 71). * a Chen prime. *an irregular prime. *a lucky prime. *the sum of five consecutive primes (7 + 11 + 13 + 17 + 19). *a Heegner number. *a Pillai prime since 18! + 1 is divisible by 67, but 67 is not one more than a multiple of 18. *palindromic in quinary (2325) and senary (1516). *a super-prime. (19 is prime) *an isolated prime. (65 and 69 aren't prime) In science *The atomic number of holmium, a lanthanide. Astronomy *Messier object Messier 67, M67, a visual magnitude, magnitude 7.5 open cluster in the constellation Cancer (constellation), Cancer. *The New General Catalogue object NGC 67, an elliptical galaxy in the constellation Andromeda (constellation), Andromeda. In music * "Car 67", a song by the band Driver 67 * Chicago (band), Chicago's song "Questions 67 and 6 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
109 (number)
109 (one hundred ndnine) is the natural number following 108 and preceding 110. In mathematics 109 is the 29th prime number. As 29 is itself prime, 109 is a super-prime. The previous prime is 107, making them both twin primes. 109 is a centered triangular number. The decimal expansion of 1/109 can be computed using the alternating series, with F(n) the n^ Fibonacci number: ::\frac=\sum_^\infty\times (-1)^=0.00917431\dots The decimal expansion of 1/109 has 108 digits, making 109 a full reptend prime in decimal. The last six digits of the 108-digit cycle are 853211, the first six Fibonacci numbers in descending order. There are exactly 109 different families of subsets of a three-element set whose union includes all three elements, 109 different loops (invertible but not necessarily associative binary operations with an identity) on six elements, and 109 squares on an infinite chessboard that can be reached by a knight within three moves. See also *109 (other) 109 ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fibonacci Number
In mathematics, the Fibonacci numbers, commonly denoted , form a sequence, the Fibonacci sequence, in which each number is the sum of the two preceding ones. The sequence commonly starts from 0 and 1, although some authors start the sequence from 1 and 1 or sometimes (as did Fibonacci) from 1 and 2. Starting from 0 and 1, the first few values in the sequence are: :0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144. The Fibonacci numbers were first described in Indian mathematics, as early as 200 BC in work by Pingala on enumerating possible patterns of Sanskrit poetry formed from syllables of two lengths. They are named after the Italian mathematician Leonardo of Pisa, later known as Fibonacci, who introduced the sequence to Western European mathematics in his 1202 book ''Liber Abaci''. Fibonacci numbers appear unexpectedly often in mathematics, so much so that there is an entire journal dedicated to their study, the ''Fibonacci Quarterly''. Applications of Fibonacci numbers include co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Closed-form Expression
In mathematics, a closed-form expression is a mathematical expression that uses a finite number of standard operations. It may contain constants, variables, certain well-known operations (e.g., + − × ÷), and functions (e.g., ''n''th root, exponent, logarithm, trigonometric functions, and inverse hyperbolic functions), but usually no limit, differentiation, or integration. The set of operations and functions may vary with author and context. Example: roots of polynomials The solutions of any quadratic equation with complex coefficients can be expressed in closed form in terms of addition, subtraction, multiplication, division, and square root extraction, each of which is an elementary function. For example, the quadratic equation :ax^2+bx+c=0, is tractable since its solutions can be expressed as a closed-form expression, i.e. in terms of elementary functions: :x=\frac. Similarly, solutions of cubic and quartic (third and fourth degree) equations can be expresse ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Golden Ratio
In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. Expressed algebraically, for quantities a and b with a > b > 0, where the Greek letter phi ( or \phi) denotes the golden ratio. The constant \varphi satisfies the quadratic equation \varphi^2 = \varphi + 1 and is an irrational number with a value of The golden ratio was called the extreme and mean ratio by Euclid, and the divine proportion by Luca Pacioli, and also goes by several other names. Mathematicians have studied the golden ratio's properties since antiquity. It is the ratio of a regular pentagon's diagonal to its side and thus appears in the construction of the dodecahedron and icosahedron. A golden rectangle—that is, a rectangle with an aspect ratio of \varphi—may be cut into a square and a smaller rectangle with the same aspect ratio. The golden ratio has been used to analyze the proportions of natural object ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadratic Polynomial
In mathematics, a quadratic polynomial is a polynomial of degree two in one or more variables. A quadratic function is the polynomial function defined by a quadratic polynomial. Before 20th century, the distinction was unclear between a polynomial and its associated polynomial function; so "quadratic polynomial" and "quadratic function" were almost synonymous. This is still the case in many elementary courses, where both terms are often abbreviated as "quadratic". For example, a univariate (single-variable) quadratic function has the form :f(x)=ax^2+bx+c,\quad a \ne 0, where is its variable. The graph of a univariate quadratic function is a parabola, a curve that has an axis of symmetry parallel to the -axis. If a quadratic function is equated with zero, then the result is a quadratic equation. The solutions of a quadratic equation are the zeros of the corresponding quadratic function. The bivariate case in terms of variables and has the form : f(x,y) = a x^2 + bx y+ c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer Sequences
In mathematics, an integer sequence is a sequence (i.e., an ordered list) of integers. An integer sequence may be specified ''explicitly'' by giving a formula for its ''n''th term, or ''implicitly'' by giving a relationship between its terms. For example, the sequence 0, 1, 1, 2, 3, 5, 8, 13, ... (the Fibonacci sequence) is formed by starting with 0 and 1 and then adding any two consecutive terms to obtain the next one: an implicit description. The sequence 0, 3, 8, 15, ... is formed according to the formula ''n''2 − 1 for the ''n''th term: an explicit definition. Alternatively, an integer sequence may be defined by a property which members of the sequence possess and other integers do not possess. For example, we can determine whether a given integer is a perfect number, even though we do not have a formula for the ''n''th perfect number. Examples Integer sequences that have their own name include: *Abundant numbers *Baum–Sweet sequence *Bell numbe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |