|
Lehmer Matrix
In mathematics, particularly matrix theory, the ''n×n'' Lehmer matrix (named after Derrick Henry Lehmer) is the constant symmetric matrix defined by :A_ = \begin i/j, & j\ge i \\ j/i, & j''n''. The values of elements diminish toward zero away from the diagonal, where all elements have value 1. The inverse of a Lehmer matrix is a tridiagonal matrix, where the superdiagonal and subdiagonal have strictly negative entries. Consider again the ''n×n'' ''A'' and ''m×m'' ''B'' Lehmer matrices, where ''m''>''n''. A rather peculiar property of their inverses is that ''A−1'' is ''nearly'' a submatrix of ''B−1'', except for the ''A−1n,n'' element, which is not equal to ''B−1n,n''. A Lehmer matrix of order ''n'' has trace ''n''. Examples The 2×2, 3×3 and 4×4 Lehmer matrices and their inverses are shown below. : \begin A_2=\begin 1 & 1/2 \\ 1/2 & 1 \end; & A_2^=\begin 4/3 & -2/3 \\ -2/3 & \end; \\ \\ A_3=\begin 1 & 1/2 & 1/3 \\ 1/2 & 1 & 2/3 \\ 1/3 & 2/ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
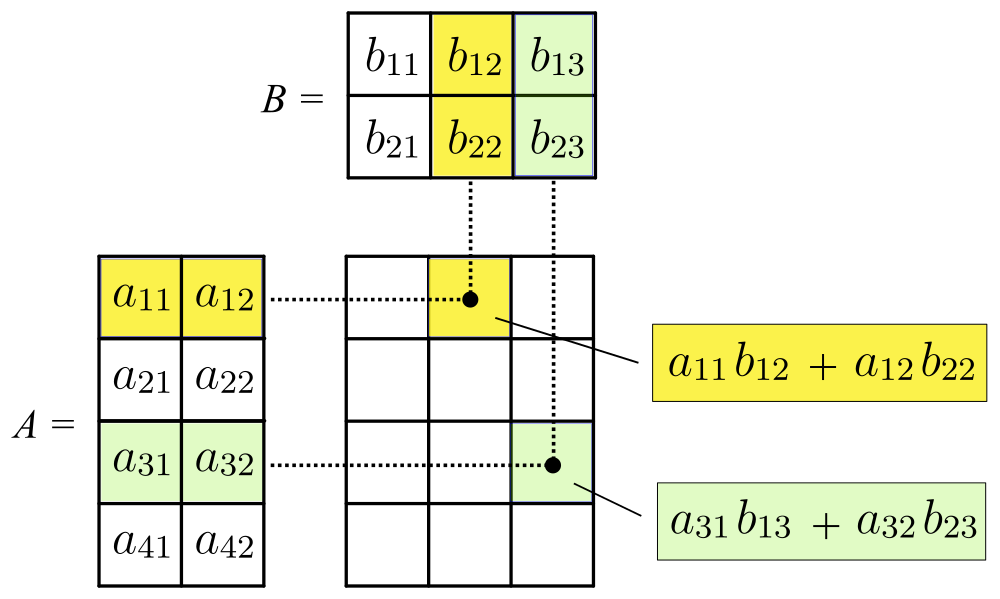
Matrix (mathematics)
In mathematics, a matrix (plural matrices) is a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns, which is used to represent a mathematical object or a property of such an object. For example, \begin1 & 9 & -13 \\20 & 5 & -6 \end is a matrix with two rows and three columns. This is often referred to as a "two by three matrix", a "-matrix", or a matrix of dimension . Without further specifications, matrices represent linear maps, and allow explicit computations in linear algebra. Therefore, the study of matrices is a large part of linear algebra, and most properties and operations of abstract linear algebra can be expressed in terms of matrices. For example, matrix multiplication represents composition of linear maps. Not all matrices are related to linear algebra. This is, in particular, the case in graph theory, of incidence matrices, and adjacency matrices. ''This article focuses on matrices related to linear algebra, and, unle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derrick Henry Lehmer
Derrick Henry "Dick" Lehmer (February 23, 1905 – May 22, 1991), almost always cited as D.H. Lehmer, was an American mathematician significant to the development of computational number theory. Lehmer refined Édouard Lucas' work in the 1930s and devised the Lucas–Lehmer primality test, Lucas–Lehmer test for Mersenne primes. His peripatetic career as a Number theory, number theorist, with him and his wife taking numerous types of work in the United States and abroad to support themselves during the Great Depression, fortuitously brought him into the center of research into early electronic computing. Early life Lehmer was born in Berkeley, California, to Derrick Norman Lehmer, a professor of mathematics at the University of California, Berkeley, and Clara Eunice Mitchell. He studied physics and earned a Bachelor degree from UC Berkeley, and continued with graduate studies at the University of Chicago. He and his father worked together on Lehmer sieves. Marriage During his s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetric Matrix
In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose. Formally, Because equal matrices have equal dimensions, only square matrices can be symmetric. The entries of a symmetric matrix are symmetric with respect to the main diagonal. So if a_ denotes the entry in the ith row and jth column then for all indices i and j. Every square diagonal matrix is symmetric, since all off-diagonal elements are zero. Similarly in characteristic different from 2, each diagonal element of a skew-symmetric matrix must be zero, since each is its own negative. In linear algebra, a real symmetric matrix represents a self-adjoint operator represented in an orthonormal basis over a real inner product space. The corresponding object for a complex inner product space is a Hermitian matrix with complex-valued entries, which is equal to its conjugate transpose. Therefore, in linear algebra over the complex numbers, it is often assumed that a symmetric matrix refe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Submatrix
In mathematics, a matrix (plural matrices) is a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns, which is used to represent a mathematical object or a property of such an object. For example, \begin1 & 9 & -13 \\20 & 5 & -6 \end is a matrix with two rows and three columns. This is often referred to as a "two by three matrix", a "-matrix", or a matrix of dimension . Without further specifications, matrices represent linear maps, and allow explicit computations in linear algebra. Therefore, the study of matrices is a large part of linear algebra, and most properties and operations of abstract linear algebra can be expressed in terms of matrices. For example, matrix multiplication represents composition of linear maps. Not all matrices are related to linear algebra. This is, in particular, the case in graph theory, of incidence matrices, and adjacency matrices. ''This article focuses on matrices related to linear algebra, and, unles ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix Inverse
In linear algebra, an -by- square matrix is called invertible (also nonsingular or nondegenerate), if there exists an -by- square matrix such that :\mathbf = \mathbf = \mathbf_n \ where denotes the -by- identity matrix and the multiplication used is ordinary matrix multiplication. If this is the case, then the matrix is uniquely determined by , and is called the (multiplicative) ''inverse'' of , denoted by . Matrix inversion is the process of finding the matrix that satisfies the prior equation for a given invertible matrix . A square matrix that is ''not'' invertible is called singular or degenerate. A square matrix is singular if and only if its determinant is zero. Singular matrices are rare in the sense that if a square matrix's entries are randomly selected from any finite region on the number line or complex plane, the probability that the matrix is singular is 0, that is, it will "almost never" be singular. Non-square matrices (-by- matrices for which ) do not hav ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tridiagonal Matrix
In linear algebra, a tridiagonal matrix is a band matrix that has nonzero elements only on the main diagonal, the subdiagonal/lower diagonal (the first diagonal below this), and the supradiagonal/upper diagonal (the first diagonal above the main diagonal). For example, the following matrix is tridiagonal: :\begin 1 & 4 & 0 & 0 \\ 3 & 4 & 1 & 0 \\ 0 & 2 & 3 & 4 \\ 0 & 0 & 1 & 3 \\ \end. The determinant of a tridiagonal matrix is given by the ''continuant'' of its elements. An orthogonal transformation of a symmetric (or Hermitian) matrix to tridiagonal form can be done with the Lanczos algorithm. Properties A tridiagonal matrix is a matrix that is both upper and lower Hessenberg matrix. In particular, a tridiagonal matrix is a direct sum of ''p'' 1-by-1 and ''q'' 2-by-2 matrices such that — the dimension of the tridiagonal. Although a general tridiagonal matrix is not necessarily symmetric or Hermitian, many of those that arise when solving linear algebra problems have one of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Superdiagonal
In geometry, a diagonal is a line segment joining two vertices of a polygon or polyhedron, when those vertices are not on the same edge. Informally, any sloping line is called diagonal. The word ''diagonal'' derives from the ancient Greek διαγώνιος ''diagonios'', "from angle to angle" (from διά- ''dia-'', "through", "across" and γωνία ''gonia'', "angle", related to ''gony'' "knee"); it was used by both Strabo and Euclid to refer to a line connecting two vertices of a rhombus or cuboid, and later adopted into Latin as ''diagonus'' ("slanting line"). In matrix algebra, the diagonal of a square matrix consists of the entries on the line from the top left corner to the bottom right corner. There are also other, non-mathematical uses. Non-mathematical uses In engineering, a diagonal brace is a beam used to brace a rectangular structure (such as scaffolding) to withstand strong forces pushing into it; although called a diagonal, due to practical considerations d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Subdiagonal
In geometry, a diagonal is a line segment joining two vertices of a polygon or polyhedron, when those vertices are not on the same edge. Informally, any sloping line is called diagonal. The word ''diagonal'' derives from the ancient Greek διαγώνιος ''diagonios'', "from angle to angle" (from διά- ''dia-'', "through", "across" and γωνία ''gonia'', "angle", related to ''gony'' "knee"); it was used by both Strabo and Euclid to refer to a line connecting two vertices of a rhombus or cuboid, and later adopted into Latin as ''diagonus'' ("slanting line"). In matrix algebra, the diagonal of a square matrix consists of the entries on the line from the top left corner to the bottom right corner. There are also other, non-mathematical uses. Non-mathematical uses In engineering, a diagonal brace is a beam used to brace a rectangular structure (such as scaffolding) to withstand strong forces pushing into it; although called a diagonal, due to practical considerations d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trace Of A Matrix
In linear algebra, the trace of a square matrix , denoted , is defined to be the sum of elements on the main diagonal (from the upper left to the lower right) of . The trace is only defined for a square matrix (). It can be proved that the trace of a matrix is the sum of its (complex) eigenvalues (counted with multiplicities). It can also be proved that for any two matrices and . This implies that similar matrices have the same trace. As a consequence one can define the trace of a linear operator mapping a finite-dimensional vector space into itself, since all matrices describing such an operator with respect to a basis are similar. The trace is related to the derivative of the determinant (see Jacobi's formula). Definition The trace of an square matrix is defined as \operatorname(\mathbf) = \sum_^n a_ = a_ + a_ + \dots + a_ where denotes the entry on the th row and th column of . The entries of can be real numbers or (more generally) complex numbers. The trace is not ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hilbert Matrix
In linear algebra, a Hilbert matrix, introduced by , is a square matrix with entries being the unit fractions : H_ = \frac. For example, this is the 5 × 5 Hilbert matrix: : H = \begin 1 & \frac & \frac & \frac & \frac \\ \frac & \frac & \frac & \frac & \frac \\ \frac & \frac & \frac & \frac & \frac \\ \frac & \frac & \frac & \frac & \frac \\ \frac & \frac & \frac & \frac & \frac \end. The Hilbert matrix can be regarded as derived from the integral : H_ = \int_0^1 x^ \, dx, that is, as a Gramian matrix for powers of ''x''. It arises in the least squares approximation of arbitrary functions by polynomials. The Hilbert matrices are canonical examples of ill-conditioned matrices, being notoriously difficult to use in numerical computation. For example, the 2-norm condition number of the matrix above is about 4.8. Historical note introduced the Hilbert matrix to study the following question in approximation theory: "Assume that , is a real interval. Is it then po ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |