|
Langer Correction
The Langer correction, named after the mathematician Rudolf Ernest Langer, is a correction to the WKB approximation for problems with radial symmetry. Description In 3D systems When applying WKB approximation method to the radial Schrödinger equation, : -\frac \frac + -V_\textrm(r)R(r) = 0 , where the effective potential is given by :V_\textrm(r)=V(r)-\frac ( \ell the azimuthal quantum number related to the angular momentum operator), the eigenenergies and the wave function behaviour obtained are different from the real solution. In 1937, Rudolf E. Langer suggested a correction :\ell(\ell+1) \rightarrow \left(\ell+\frac\right)^2 which is known as Langer correction or Langer replacement. This manipulation is equivalent to inserting a 1/4 constant factor whenever \ell(\ell+1) appears. Heuristically, it is said that this factor arises because the range of the radial Schrödinger equation is restricted from 0 to infinity, as opposed to the entire real line. By such a changi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rudolf Ernest Langer
Rudolf Ernest Langer (8 March 1894 – 11 March 1968) was an American mathematician, known for the Langer correction and as a president of the Mathematical Association of America. Career Langer, the elder brother of William L. Langer, earned his PhD in 1922 from Harvard University under G. D. Birkhoff. He taught mathematics at Dartmouth College from 1922 to 1925. From 1927 to 1964 he was a mathematics professor at the University of Wisconsin-Madison and, from 1942 to 1952, the chair of the mathematics department. From 1956 to 1963 he was the director of the Army Mathematics Research Center; he was succeeded as director by J. Barkley Rosser. Langer's doctoral students include Homer Newell, Jr. and Henry Scheffé Henry Scheffé (April 11, 1907 – July 5, 1977) was an American statistician. He is known for the Lehmann–Scheffé theorem and Scheffé's method. Education and career Scheffé was born in New York City on April 11, 1907, the child of Germa .... Works * * * * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
WKB Approximation
In mathematical physics, the WKB approximation or WKB method is a method for finding approximate solutions to linear differential equations with spatially varying coefficients. It is typically used for a semiclassical calculation in quantum mechanics in which the wavefunction is recast as an exponential function, semiclassically expanded, and then either the amplitude or the phase is taken to be changing slowly. The name is an initialism for Wentzel–Kramers–Brillouin. It is also known as the LG or Liouville–Green method. Other often-used letter combinations include JWKB and WKBJ, where the "J" stands for Jeffreys. Brief history This method is named after physicists Gregor Wentzel, Hendrik Anthony Kramers, and Léon Brillouin, who all developed it in 1926. In 1923, mathematician Harold Jeffreys had developed a general method of approximating solutions to linear, second-order differential equations, a class that includes the Schrödinger equation. The Schrödinger equat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schrödinger Equation
The Schrödinger equation is a linear partial differential equation that governs the wave function of a quantum-mechanical system. It is a key result in quantum mechanics, and its discovery was a significant landmark in the development of the subject. The equation is named after Erwin Schrödinger, who postulated the equation in 1925, and published it in 1926, forming the basis for the work that resulted in his Nobel Prize in Physics in 1933. Conceptually, the Schrödinger equation is the quantum counterpart of Newton's second law in classical mechanics. Given a set of known initial conditions, Newton's second law makes a mathematical prediction as to what path a given physical system will take over time. The Schrödinger equation gives the evolution over time of a wave function, the quantum-mechanical characterization of an isolated physical system. The equation can be derived from the fact that the time-evolution operator must be unitary, and must therefore be generated ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
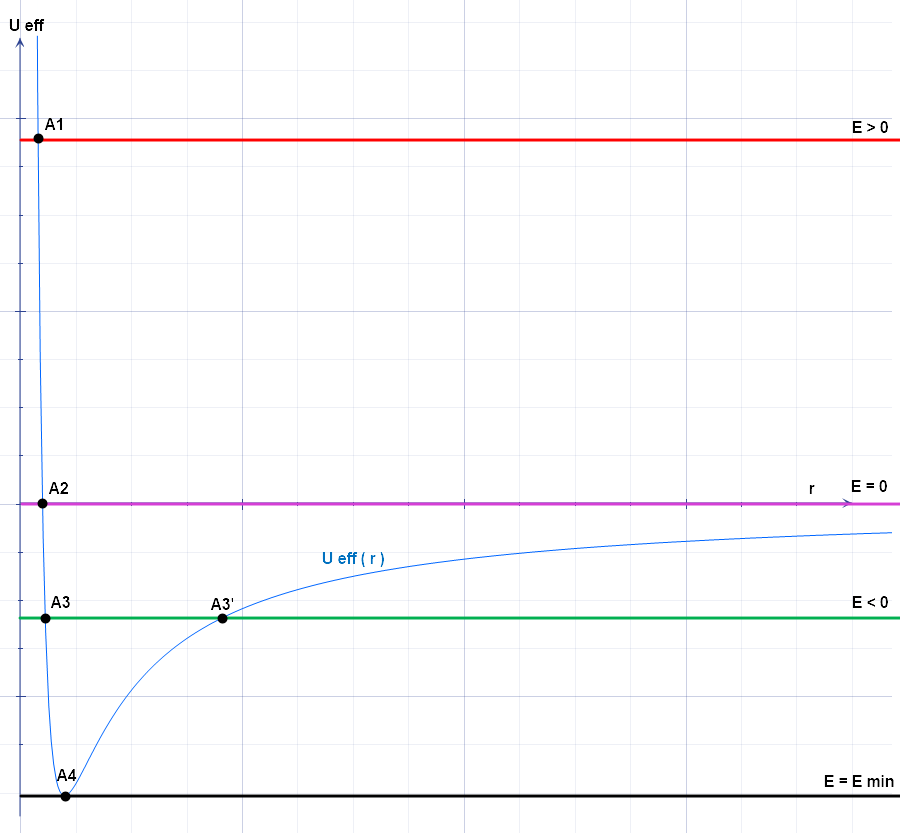
Effective Potential
The effective potential (also known as effective potential energy) combines multiple, perhaps opposing, effects into a single potential. In its basic form, it is the sum of the 'opposing' centrifugal potential energy with the potential energy of a dynamical system. It may be used to determine the orbits of planets (both Newtonian and relativistic) and to perform semi-classical atomic calculations, and often allows problems to be reduced to fewer dimensions. Definition The basic form of potential U_\text is defined as: U_\text(\mathbf) = \frac + U(\mathbf), where *''L'' is the angular momentum *''r'' is the distance between the two masses *''μ'' is the reduced mass of the two bodies (approximately equal to the mass of the orbiting body if one mass is much larger than the other); and *''U''(''r'') is the general form of the potential. The effective force, then, is the negative gradient of the effective potential: \begin \mathbf_\text &= -\nabla U_\text(\mathbf) \\ &= \frac \ha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Azimuthal Quantum Number
The azimuthal quantum number is a quantum number for an atomic orbital that determines its angular momentum operator, orbital angular momentum and describes the shape of the orbital. The wikt:azimuthal, azimuthal quantum number is the second of a set of quantum numbers that describe the unique quantum state of an electron (the others being the principal quantum number, the magnetic quantum number, and the spin quantum number). It is also known as the orbital angular momentum quantum number, orbital quantum number or second quantum number, and is symbolized as ℓ (pronounced ''ell''). Derivation Connected with the energy states of the atom's electrons are four quantum numbers: ''n'', ''ℓ'', ''m''''ℓ'', and ''m''''s''. These specify the complete, unique quantum state of a single electron in an atom, and make up its wavefunction or ''orbital''. When solving to obtain the wave function, the Schrödinger equation reduces to three equations that lead to the first three quantum ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Momentum Operator
In quantum mechanics, the angular momentum operator is one of several related operators analogous to classical angular momentum. The angular momentum operator plays a central role in the theory of atomic and molecular physics and other quantum problems involving rotational symmetry. Such an operator is applied to a mathematical representation of the physical state of a system and yields an angular momentum value if the state has a definite value for it. In both classical and quantum mechanical systems, angular momentum (together with linear momentum and energy) is one of the three fundamental properties of motion.Introductory Quantum Mechanics, Richard L. Liboff, 2nd Edition, There are several angular momentum operators: total angular momentum (usually denoted J), orbital angular momentum (usually denoted L), and spin angular momentum (spin for short, usually denoted S). The term ''angular momentum operator'' can (confusingly) refer to either the total or the orbital angular mom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regge Trajectories
Regge may refer to * Tullio Regge (1931-2014), Italian physicist, developer of Regge calculus and Regge theory * Regge calculus, formalism for producing simplicial approximations of spacetimes * Regge theory, study of the analytic properties of scattering * 3778 Regge, main-belt asteroid * Regge (river) The Regge rɛɣəis a river in the Netherlands. It is a tributary to the Vecht of Overijssel. The source of the Regge is near the town Goor. It flows north through Rijssen, Nijverdal, and Hellendoorn. The Regge joins the Vecht near Ommen Omm ..., river in Overijssel, the Netherlands {{disambig, surname Surnames of Italian origin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Yukawa Potential
In particle, atomic and condensed matter physics, a Yukawa potential (also called a screened Coulomb potential) is a potential named after the Japanese physicist Hideki Yukawa. The potential is of the form: :V_\text(r)= -g^2\frac, where is a magnitude scaling constant, i.e. is the amplitude of potential, is the mass of the particle, is the radial distance to the particle, and is another scaling constant, so that r \approx \tfrac is the approximate range. The potential is monotonically increasing in and it is negative, implying the force is attractive. In the SI system, the unit of the Yukawa potential is (1/meters). The Coulomb potential of electromagnetism is an example of a Yukawa potential with the e^ factor equal to 1, everywhere. This can be interpreted as saying that the photon mass is equal to 0. The photon is the force-carrier between interacting, charged particles. In interactions between a meson field and a fermion field, the constant is equal to the gauge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harald J
Harald or Haraldr is the Old Norse form of the given name Harold. It may refer to: Medieval Kings of Denmark * Harald Bluetooth (935–985/986) Kings of Norway * Harald Fairhair (c. 850–c. 933) * Harald Greycloak (died 970) * Harald Hardrada (1015–1066) * Harald Gille (reigned 1130–1136) Grand Dukes of Kiev * Mstislav the Great (1076–1132), known as Harald in Norse sagas King of Mann and the Isles * Haraldr Óláfsson (died 1248) Earls of Orkney * Harald Haakonsson (died 1131) * Harald Maddadsson (–1206) * Harald Eiriksson Others * Hagrold (fl. 944–954), also known as Harald, Scandinavian chieftain in Normandy * Harald Grenske (10th century), petty king in Vestfold in Norway * Harald Klak (–), king in Jutland * Harald Wartooth, legendary king of Sweden, Denmark and Norway * Harald the Younger, 9th-century Viking leader Modern name Royalty * Harald V of Norway (born 1937), present King of Norway * Prince Harald of Denmark (1876–1949) Arts and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Einstein–Brillouin–Keller Method
The Einstein–Brillouin–Keller method (EBK) is a semiclassical method (named after Albert Einstein, Léon Brillouin, and Joseph B. Keller) used to compute eigenvalues in quantum-mechanical systems. EBK quantization is an improvement from Bohr-Sommerfeld quantization which did not consider the caustic phase jumps at classical turning points. This procedure is able to reproduce exactly the spectrum of the 3D harmonic oscillator, particle in a box, and even the relativistic fine structure of the hydrogen atom. In 1976–1977, Michael Berry and M. Tabor derived an extension to Gutzwiller trace formula for the density of states of an integrable system starting from EBK quantization. There have been a number of recent results on computational issues related to this topic, for example, the work of Eric J. Heller and Emmanuel David Tannenbaum using a partial differential equation gradient descent approach. Procedure Given a separable classical system defined by coordinat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.png)