|
Kunita–Watanabe Inequality
In stochastic calculus, the Kunita–Watanabe inequality is a generalization of the Cauchy–Schwarz inequality to integrals of stochastic processes. It was first obtained by Hiroshi Kunita and Shinzo Watanabe Shinzō Watanabe (渡辺 信三 Watanabe Shinzō, 23 December 1935) is a Japanese mathematician, who has made fundamental contributions to probability theory, stochastic processes and stochastic differential equations. He is regarded and revere ... and plays a fundamental role in their extension of Ito's stochastic integral to square-integrable martingales. Statement of the theorem Let ''M'', ''N'' be continuous local martingales and ''H'', ''K'' measurable processes. Then : \int_0^t \left, H_s \ \left, K_s \ \left, \mathrm \langle M,N \rangle_s \ \leq \sqrt \sqrt where the angled brackets indicates the quadratic variation and quadratic covariation operators. The integrals are understood in the Lebesgue–Stieltjes sense. References * {{DEFAULTSORT:Kunit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stochastic Calculus
Stochastic calculus is a branch of mathematics that operates on stochastic processes. It allows a consistent theory of integration to be defined for integrals of stochastic processes with respect to stochastic processes. This field was created and started by the Japanese mathematician Kiyoshi Itô during World War II. The best-known stochastic process to which stochastic calculus is applied is the Wiener process (named in honor of Norbert Wiener), which is used for modeling Brownian motion as described by Louis Bachelier in 1900 and by Albert Einstein in 1905 and other physical diffusion processes in space of particles subject to random forces. Since the 1970s, the Wiener process has been widely applied in financial mathematics and economics to model the evolution in time of stock prices and bond interest rates. The main flavours of stochastic calculus are the Itô calculus and its variational relative the Malliavin calculus. For technical reasons the Itô integral is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
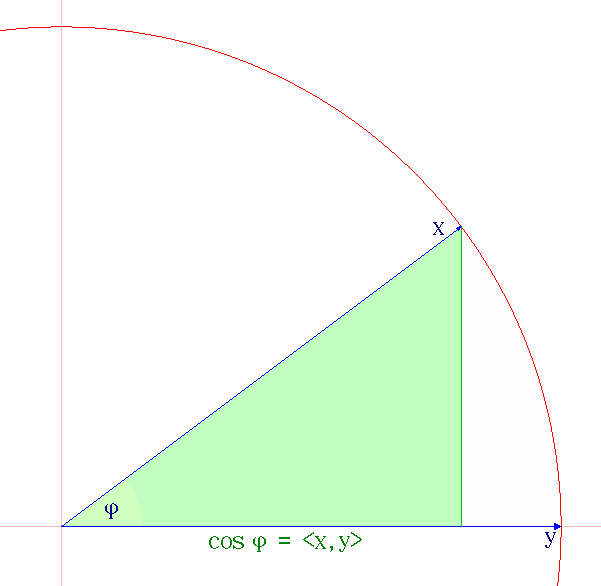
Cauchy–Schwarz Inequality
The Cauchy–Schwarz inequality (also called Cauchy–Bunyakovsky–Schwarz inequality) is considered one of the most important and widely used inequalities in mathematics. The inequality for sums was published by . The corresponding inequality for integrals was published by and . Schwarz gave the modern proof of the integral version. Statement of the inequality The Cauchy–Schwarz inequality states that for all vectors \mathbf and \mathbf of an inner product space it is true that where \langle \cdot, \cdot \rangle is the inner product. Examples of inner products include the real and complex dot product; see the examples in inner product. Every inner product gives rise to a norm, called the or , where the norm of a vector \mathbf is denoted and defined by: \, \mathbf\, := \sqrt so that this norm and the inner product are related by the defining condition \, \mathbf\, ^2 = \langle \mathbf, \mathbf \rangle, where \langle \mathbf, \mathbf \rangle is always a non-nega ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stochastic Processes
In probability theory and related fields, a stochastic () or random process is a mathematical object usually defined as a family of random variables. Stochastic processes are widely used as mathematical models of systems and phenomena that appear to vary in a random manner. Examples include the growth of a bacterial population, an electrical current fluctuating due to thermal noise, or the movement of a gas molecule. Stochastic processes have applications in many disciplines such as biology, chemistry, ecology, neuroscience, physics, image processing, signal processing, control theory, information theory, computer science, cryptography and telecommunications. Furthermore, seemingly random changes in financial markets have motivated the extensive use of stochastic processes in finance. Applications and the study of phenomena have in turn inspired the proposal of new stochastic processes. Examples of such stochastic processes include the Wiener process or Browni ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shinzo Watanabe
Shinzō Watanabe (渡辺 信三 Watanabe Shinzō, 23 December 1935) is a Japanese mathematician, who has made fundamental contributions to probability theory, stochastic processes and stochastic differential equations. He is regarded and revered as one of the fundamental contributors to the modern probability theory and Stochastic calculus. The pioneering book “Stochastic Differential Equations and Diffusion Processes” he wrote with Nobuyuki Ikeda has attracted a lot of researchers into the area and is known as the “Ikeda-Watanabe” for researchers in the field of stochastic analysis. He had been served as the editor of Springer Mathematics. Biography Watanabe received his bachelor's degree from Kyoto University in 1958 and completed his Ph.D. under Kiyosi Itô in 1963. Watanabe subsequently became a professor at Kyoto University. He was also a visiting professor at Stanford University and participated in the organizing committees of international Japanese/Soviet ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stochastic Integral
Stochastic calculus is a branch of mathematics that operates on stochastic processes. It allows a consistent theory of integration to be defined for integrals of stochastic processes with respect to stochastic processes. This field was created and started by the Japanese mathematician Kiyoshi Itô during World War II. The best-known stochastic process to which stochastic calculus is applied is the Wiener process (named in honor of Norbert Wiener), which is used for modeling Brownian motion as described by Louis Bachelier in 1900 and by Albert Einstein in 1905 and other physical diffusion processes in space of particles subject to random forces. Since the 1970s, the Wiener process has been widely applied in financial mathematics and economics to model the evolution in time of stock prices and bond interest rates. The main flavours of stochastic calculus are the Itô calculus and its variational relative the Malliavin calculus. For technical reasons the Itô integral is the mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Local Martingale
In mathematics, a local martingale is a type of stochastic process, satisfying the localized version of the martingale property. Every martingale is a local martingale; every bounded local martingale is a martingale; in particular, every local martingale that is bounded from below is a supermartingale, and every local martingale that is bounded from above is a submartingale; however, in general a local martingale is not a martingale, because its expectation can be distorted by large values of small probability. In particular, a driftless diffusion process is a local martingale, but not necessarily a martingale. Local martingales are essential in stochastic analysis (see Itō calculus, semimartingale, and Girsanov theorem). Definition Let (\Omega,F,P) be a probability space; let F_*=\ be a filtration of F; let X: stopping rule">stopping times \tau_k : \Omega \to [0,\infty) such that * the \tau_k are almost surely increasing: P\left\=1; * the \tau_k diverge almost surely: P \lef ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Measurable
In mathematics, the concept of a measure is a generalization and formalization of geometrical measures (length, area, volume) and other common notions, such as mass and probability of events. These seemingly distinct concepts have many similarities and can often be treated together in a single mathematical context. Measures are foundational in probability theory, integration theory, and can be generalized to assume negative values, as with electrical charge. Far-reaching generalizations (such as spectral measures and projection-valued measures) of measure are widely used in quantum physics and physics in general. The intuition behind this concept dates back to ancient Greece, when Archimedes tried to calculate the area of a circle. But it was not until the late 19th and early 20th centuries that measure theory became a branch of mathematics. The foundations of modern measure theory were laid in the works of Émile Borel, Henri Lebesgue, Nikolai Luzin, Johann Radon, Cons ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadratic Variation
In mathematics, quadratic variation is used in the analysis of stochastic processes such as Brownian motion and other martingales. Quadratic variation is just one kind of variation of a process. Definition Suppose that X_t is a real-valued stochastic process defined on a probability space (\Omega,\mathcal,\mathbb) and with time index t ranging over the non-negative real numbers. Its quadratic variation is the process, written as t, defined as : t=\lim_\sum_^n(X_-X_)^2 where P ranges over partitions of the interval ,t/math> and the norm of the partition P is the mesh. This limit, if it exists, is defined using convergence in probability. Note that a process may be of finite quadratic variation in the sense of the definition given here and its paths be nonetheless almost surely of infinite 1-variation for every t>0 in the classical sense of taking the supremum of the sum over all partitions; this is in particular the case for Brownian motion. More generally, the covariation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lebesgue–Stieltjes Integration
In measure-theoretic analysis and related branches of mathematics, Lebesgue–Stieltjes integration generalizes both Riemann–Stieltjes and Lebesgue integration, preserving the many advantages of the former in a more general measure-theoretic framework. The Lebesgue–Stieltjes integral is the ordinary Lebesgue integral with respect to a measure known as the Lebesgue–Stieltjes measure, which may be associated to any function of bounded variation on the real line. The Lebesgue–Stieltjes measure is a regular Borel measure, and conversely every regular Borel measure on the real line is of this kind. Lebesgue–Stieltjes integrals, named for Henri Leon Lebesgue and Thomas Joannes Stieltjes, are also known as Lebesgue–Radon integrals or just Radon integrals, after Johann Radon, to whom much of the theory is due. They find common application in probability and stochastic processes, and in certain branches of analysis including potential theory. Definition The Lebesgue– ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Theorems
Probability is the branch of mathematics concerning numerical descriptions of how likely an event is to occur, or how likely it is that a proposition is true. The probability of an event is a number between 0 and 1, where, roughly speaking, 0 indicates impossibility of the event and 1 indicates certainty."Kendall's Advanced Theory of Statistics, Volume 1: Distribution Theory", Alan Stuart and Keith Ord, 6th Ed, (2009), .William Feller, ''An Introduction to Probability Theory and Its Applications'', (Vol 1), 3rd Ed, (1968), Wiley, . The higher the probability of an event, the more likely it is that the event will occur. A simple example is the tossing of a fair (unbiased) coin. Since the coin is fair, the two outcomes ("heads" and "tails") are both equally probable; the probability of "heads" equals the probability of "tails"; and since no other outcomes are possible, the probability of either "heads" or "tails" is 1/2 (which could also be written as 0.5 or 50%). These con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |