|
K-SVD
In applied mathematics, K-SVD is a dictionary learning algorithm for creating a dictionary for sparse representations, via a singular value decomposition approach. K-SVD is a generalization of the k-means clustering method, and it works by iteratively alternating between sparse coding the input data based on the current dictionary, and updating the atoms in the dictionary to better fit the data. It is structurally related to the expectation maximization (EM) algorithm. K-SVD can be found widely in use in applications such as image processing, audio processing, biology, and document analysis. K-SVD algorithm K-SVD is a kind of generalization of K-means, as follows. The k-means clustering can be also regarded as a method of sparse representation. That is, finding the best possible codebook to represent the data samples \^M_ by Nearest neighbor search, nearest neighbor, by solving : \quad \min \limits _ \ \qquad \text \forall i, x_i = e_k \text k. which is equivalent to : ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dictionary Learning
Sparse coding is a representation learning method which aims at finding a sparse representation of the input data (also known as sparse coding) in the form of a linear combination of basic elements as well as those basic elements themselves. These elements are called ''atoms'' and they compose a ''dictionary''. Atoms in the dictionary are not required to be orthogonal, and they may be an over-complete spanning set. This problem setup also allows the dimensionality of the signals being represented to be higher than the one of the signals being observed. The above two properties lead to having seemingly redundant atoms that allow multiple representations of the same signal but also provide an improvement in sparsity and flexibility of the representation. One of the most important applications of sparse dictionary learning is in the field of compressed sensing or signal recovery. In compressed sensing, a high-dimensional signal can be recovered with only a few linear measurements pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sparse Representation
Sparse approximation (also known as sparse representation) theory deals with sparse solutions for systems of linear equations. Techniques for finding these solutions and exploiting them in applications have found wide use in image processing, signal processing, machine learning, medical imaging, and more. Sparse decomposition Noiseless observations Consider a linear system of equations x = D\alpha, where D is an underdetermined m\times p matrix (m < p) and . The matrix (typically assumed to be full-rank) is referred to as the dictionary, and is a signal of interest. The core sparse representation problem is defined as the quest for the sparsest possible representation satisfying . Due to the underdetermined nature of , this linear system admits in general infinitely many possible solutions, and among these we seek the one with the fewe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Singular Value Decomposition
In linear algebra, the singular value decomposition (SVD) is a factorization of a real or complex matrix. It generalizes the eigendecomposition of a square normal matrix with an orthonormal eigenbasis to any \ m \times n\ matrix. It is related to the polar decomposition. Specifically, the singular value decomposition of an \ m \times n\ complex matrix is a factorization of the form \ \mathbf = \mathbf\ , where is an \ m \times m\ complex unitary matrix, \ \mathbf\ is an \ m \times n\ rectangular diagonal matrix with non-negative real numbers on the diagonal, is an n \times n complex unitary matrix, and \ \mathbf\ is the conjugate transpose of . Such decomposition always exists for any complex matrix. If is real, then and can be guaranteed to be real orthogonal matrices; in such contexts, the SVD is often denoted \ \mathbf^\mathsf\ . The diagonal entries \ \sigma_i = \Sigma_\ of \ \mathbf\ are uniquely determined by and are known as the singular values of . The n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
K-means Clustering
''k''-means clustering is a method of vector quantization, originally from signal processing, that aims to partition ''n'' observations into ''k'' clusters in which each observation belongs to the cluster with the nearest mean (cluster centers or cluster centroid), serving as a prototype of the cluster. This results in a partitioning of the data space into Voronoi cells. ''k''-means clustering minimizes within-cluster variances (squared Euclidean distances), but not regular Euclidean distances, which would be the more difficult Weber problem: the mean optimizes squared errors, whereas only the geometric median minimizes Euclidean distances. For instance, better Euclidean solutions can be found using k-medians and k-medoids. The problem is computationally difficult (NP-hard); however, efficient heuristic algorithms converge quickly to a local optimum. These are usually similar to the expectation-maximization algorithm for mixtures of Gaussian distributions via an iterative refine ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
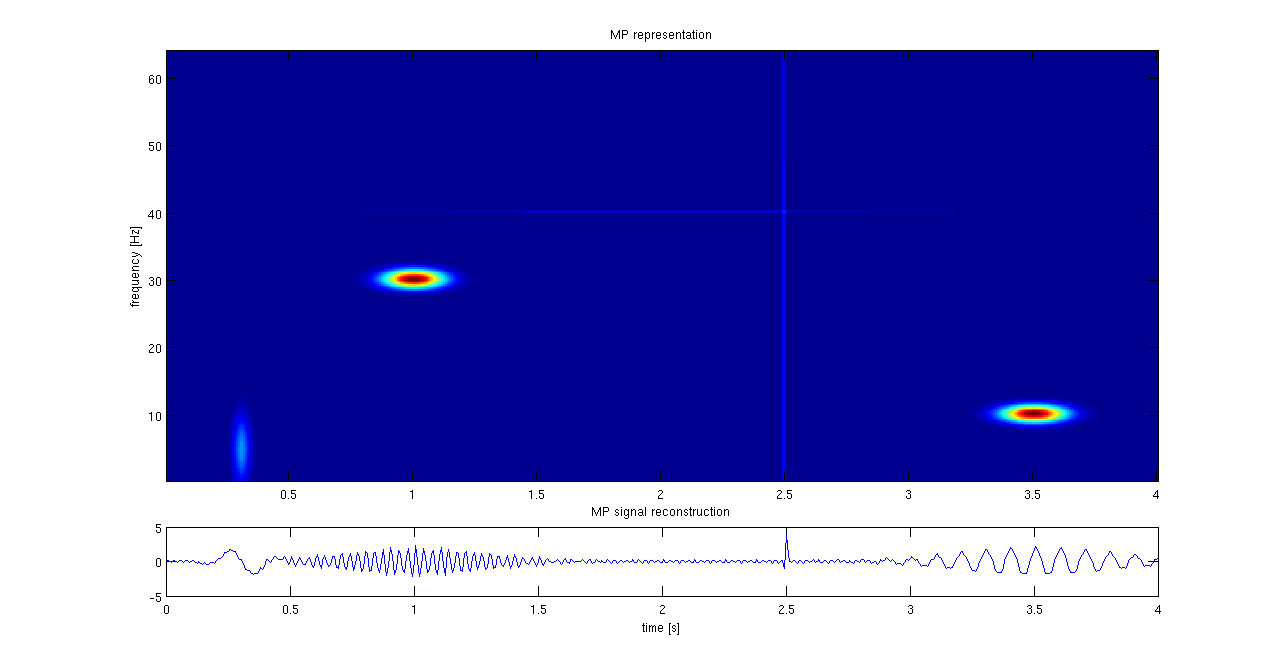
Matching Pursuit
Matching pursuit (MP) is a sparse approximation algorithm which finds the "best matching" projections of multidimensional data onto the span of an over-complete (i.e., redundant) dictionary D. The basic idea is to approximately represent a signal f from Hilbert space H as a weighted sum of finitely many functions g_ (called atoms) taken from D. An approximation with N atoms has the form : f(t) \approx \hat f_N(t) := \sum_^ a_n g_(t) where g_ is the \gamma_nth column of the matrix D and a_n is the scalar weighting factor (amplitude) for the atom g_. Normally, not every atom in D will be used in this sum. Instead, matching pursuit chooses the atoms one at a time in order to maximally (greedily) reduce the approximation error. This is achieved by finding the atom that has the highest inner product with the signal (assuming the atoms are normalized), subtracting from the signal an approximation that uses only that one atom, and repeating the process until the signal is satisfactorily d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sparse Approximation
Sparse approximation (also known as sparse representation) theory deals with sparse solutions for systems of linear equations. Techniques for finding these solutions and exploiting them in applications have found wide use in image processing, signal processing, machine learning, medical imaging, and more. Sparse decomposition Noiseless observations Consider a linear system of equations x = D\alpha, where D is an underdetermined m\times p matrix (m < p) and . The matrix (typically assumed to be full-rank) is referred to as the dictionary, and is a signal of interest. The core sparse representation problem is defined as the quest for the sparsest possible representation satisfying . Due to the underdetermined nature of , this linear system admits in general infinitely many possible solutions, and among these we seek the one with the fewe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Singular Value Decomposition
In linear algebra, the singular value decomposition (SVD) is a factorization of a real or complex matrix. It generalizes the eigendecomposition of a square normal matrix with an orthonormal eigenbasis to any \ m \times n\ matrix. It is related to the polar decomposition. Specifically, the singular value decomposition of an \ m \times n\ complex matrix is a factorization of the form \ \mathbf = \mathbf\ , where is an \ m \times m\ complex unitary matrix, \ \mathbf\ is an \ m \times n\ rectangular diagonal matrix with non-negative real numbers on the diagonal, is an n \times n complex unitary matrix, and \ \mathbf\ is the conjugate transpose of . Such decomposition always exists for any complex matrix. If is real, then and can be guaranteed to be real orthogonal matrices; in such contexts, the SVD is often denoted \ \mathbf^\mathsf\ . The diagonal entries \ \sigma_i = \Sigma_\ of \ \mathbf\ are uniquely determined by and are known as the singular values of . The n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Applied Mathematics
Applied mathematics is the application of mathematical methods by different fields such as physics, engineering, medicine, biology, finance, business, computer science, and industry. Thus, applied mathematics is a combination of mathematical science and specialized knowledge. The term "applied mathematics" also describes the professional specialty in which mathematicians work on practical problems by formulating and studying mathematical models. In the past, practical applications have motivated the development of mathematical theories, which then became the subject of study in pure mathematics where abstract concepts are studied for their own sake. The activity of applied mathematics is thus intimately connected with research in pure mathematics. History Historically, applied mathematics consisted principally of applied analysis, most notably differential equations; approximation theory (broadly construed, to include representations, asymptotic methods, variational ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expectation Maximization
Expectation or Expectations may refer to: Science * Expectation (epistemic) * Expected value, in mathematical probability theory * Expectation value (quantum mechanics) * Expectation–maximization algorithm, in statistics Music * ''Expectation'' (album), a 2013 album by Girl's Day * ''Expectation'', a 2006 album by Matt Harding * ''Expectations'' (Keith Jarrett album), 1971 * ''Expectations'' (Dance Exponents album), 1985 * ''Expectations'' (Hayley Kiyoko album), 2018 **"Expectations/Overture", a song from the album * ''Expectations'' (Bebe Rexha album), 2018 * ''Expectations'' (Katie Pruitt album), 2020 **"Expectations", a song from the album * "Expectation" (waltz), a 1980 waltz composed by Ilya Herold Lavrentievich Kittler * "Expectation" (song), a 2010 song by Tame Impala * "Expectations" (song), a 2018 song by Lauren Jauregui * "Expectations", a song by Three Days Grace from ''Transit of Venus'', 2012 See also *''Great Expectations'', a novel by Charles Dickens *''X ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nearest Neighbor Search
Nearest neighbor search (NNS), as a form of proximity search, is the optimization problem of finding the point in a given set that is closest (or most similar) to a given point. Closeness is typically expressed in terms of a dissimilarity function: the less similar the objects, the larger the function values. Formally, the nearest-neighbor (NN) search problem is defined as follows: given a set ''S'' of points in a space ''M'' and a query point ''q'' ∈ ''M'', find the closest point in ''S'' to ''q''. Donald Knuth in vol. 3 of ''The Art of Computer Programming'' (1973) called it the post-office problem, referring to an application of assigning to a residence the nearest post office. A direct generalization of this problem is a ''k''-NN search, where we need to find the ''k'' closest points. Most commonly ''M'' is a metric space and dissimilarity is expressed as a distance metric, which is symmetric and satisfies the triangle inequality. Even more common, ''M'' is taken ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frobenius Norm
In mathematics, a matrix norm is a vector norm in a vector space whose elements (vectors) are matrices (of given dimensions). Preliminaries Given a field K of either real or complex numbers, let K^ be the -vector space of matrices with m rows and n columns and entries in the field K. A matrix norm is a norm on K^. This article will always write such norms with double vertical bars (like so: \, A\, ). Thus, the matrix norm is a function \, \cdot\, : K^ \to \R that must satisfy the following properties: For all scalars \alpha \in K and matrices A, B \in K^, *\, A\, \ge 0 (''positive-valued'') *\, A\, = 0 \iff A=0_ (''definite'') *\left\, \alpha A\right\, =\left, \alpha\ \left\, A\right\, (''absolutely homogeneous'') *\, A+B\, \le \, A\, +\, B\, (''sub-additive'' or satisfying the ''triangle inequality'') The only feature distinguishing matrices from rearranged vectors is multiplication. Matrix norms are particularly useful if they are also sub-multiplicative: *\left\, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix Norm
In mathematics, a matrix norm is a vector norm in a vector space whose elements (vectors) are matrices (of given dimensions). Preliminaries Given a field K of either real or complex numbers, let K^ be the -vector space of matrices with m rows and n columns and entries in the field K. A matrix norm is a norm on K^. This article will always write such norms with double vertical bars (like so: \, A\, ). Thus, the matrix norm is a function \, \cdot\, : K^ \to \R that must satisfy the following properties: For all scalars \alpha \in K and matrices A, B \in K^, *\, A\, \ge 0 (''positive-valued'') *\, A\, = 0 \iff A=0_ (''definite'') *\left\, \alpha A\right\, =\left, \alpha\ \left\, A\right\, (''absolutely homogeneous'') *\, A+B\, \le \, A\, +\, B\, (''sub-additive'' or satisfying the ''triangle inequality'') The only feature distinguishing matrices from rearranged vectors is multiplication. Matrix norms are particularly useful if they are also sub-multiplicative: *\left\, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |