|
Jeans Instability
The Jeans instability is a concept in astrophysics that describes an instability that leads to the gravitational collapse of a cloud of gas or dust. It causes the collapse of interstellar gas clouds and subsequent star formation. It occurs when the internal gas pressure is not strong enough to prevent the gravitational collapse of a region filled with matter. It is named after James Jeans. For stability, the cloud must be in hydrostatic equilibrium, which in case of a spherical cloud translates to \frac=-\frac, where M_\text(r) is the enclosed mass, ''p'' is the pressure, \rho(r) is the density of the gas (at radius ''r''), ''G'' is the gravitational constant, and ''r'' is the radius. The equilibrium is stable if small perturbations are damped and unstable if they are amplified. In general, the cloud is unstable if it is either very massive at a given temperature or very cool at a given mass; under these circumstances, the gas pressure gradient cannot overcome gravitational fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Astrophysics
Astrophysics is a science that employs the methods and principles of physics and chemistry in the study of astronomical objects and phenomena. As one of the founders of the discipline, James Keeler, said, astrophysics "seeks to ascertain the nature of the heavenly bodies, rather than their positions or motions in space—''what'' they are, rather than ''where'' they are", which is studied in celestial mechanics. Among the subjects studied are the Sun ( solar physics), other stars, galaxies, extrasolar planets, the interstellar medium, and the cosmic microwave background. Emissions from these objects are examined across all parts of the electromagnetic spectrum, and the properties examined include luminosity, density, temperature, and chemical composition. Because astrophysics is a very broad subject, ''astrophysicists'' apply concepts and methods from many disciplines of physics, including classical mechanics, electromagnetism, statistical mechanics, thermodynamics, quantum ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Temperature
Temperature is a physical quantity that quantitatively expresses the attribute of hotness or coldness. Temperature is measurement, measured with a thermometer. It reflects the average kinetic energy of the vibrating and colliding atoms making up a substance. Thermometers are calibrated in various temperature scales that historically have relied on various reference points and thermometric substances for definition. The most common scales are the Celsius scale with the unit symbol °C (formerly called ''centigrade''), the Fahrenheit scale (°F), and the Kelvin scale (K), with the third being used predominantly for scientific purposes. The kelvin is one of the seven base units in the International System of Units (SI). Absolute zero, i.e., zero kelvin or −273.15 °C, is the lowest point in the thermodynamic temperature scale. Experimentally, it can be approached very closely but not actually reached, as recognized in the third law of thermodynamics. It would be impossible ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bonnor–Ebert Mass
In astrophysics, the Bonnor–Ebert mass is the largest mass that an isothermal gas sphere embedded in a pressurized medium can have while still remaining in hydrostatic equilibrium. Clouds of gas with masses greater than the Bonnor–Ebert mass must inevitably undergo gravitational collapse to form much smaller and denser objects. As the gravitational collapse of an interstellar gas cloud is the first stage in the formation of a protostar, the Bonnor–Ebert mass is an important quantity in the study of star formation. For a gas cloud embedded in a medium with a gas pressure p_, the Bonnor–Ebert mass is given by M_ (p_0)= where G is the gravitational constant and c_s \equiv \sqrt is the isothermal sound speed (\gamma = 1) with \mu as the molecular mass. a is a dimensionless constant which varies based on the density distribution of the cloud. For a uniform mass density a=1 and for a centrally peaked density a\approx 1.67. See also * Jeans mass The Jeans instability is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adiabatic Index
In thermal physics and thermodynamics, the heat capacity ratio, also known as the adiabatic index, the ratio of specific heats, or Laplace's coefficient, is the ratio of the heat capacity at constant pressure () to heat capacity at constant volume (). It is sometimes also known as the ''isentropic expansion factor'' and is denoted by (gamma) for an ideal gasγ first appeared in an article by the French mathematician, engineer, and physicist Siméon Denis Poisson: * On p. 332, Poisson defines γ merely as a small deviation from equilibrium which causes small variations of the equilibrium value of the density ρ. In Poisson's article of 1823 – * γ was expressed as a function of density D (p. 8) or of pressure P (p. 9). Meanwhile, in 1816 the French mathematician and physicist Pierre-Simon Laplace had found that the speed of sound depends on the ratio of the specific heats. * However, he didn't denote the ratio as γ. In 1825, Laplace stated that the speed of sound is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equation Of State
In physics and chemistry, an equation of state is a thermodynamic equation relating state variables, which describe the state of matter under a given set of physical conditions, such as pressure, volume, temperature, or internal energy. Most modern equations of state are formulated in the Helmholtz free energy. Equations of state are useful in describing the properties of pure substances and mixtures in liquids, gases, and solid states as well as the state of matter in the interior of stars. Though there are many equations of state, none accurately predicts properties of substances under all conditions. The quest for a universal equation of state has spanned three centuries. Overview At present, there is no single equation of state that accurately predicts the properties of all substances under all conditions. An example of an equation of state correlates densities of gases and liquids to temperatures and pressures, known as the ideal gas law, which is roughly accurate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
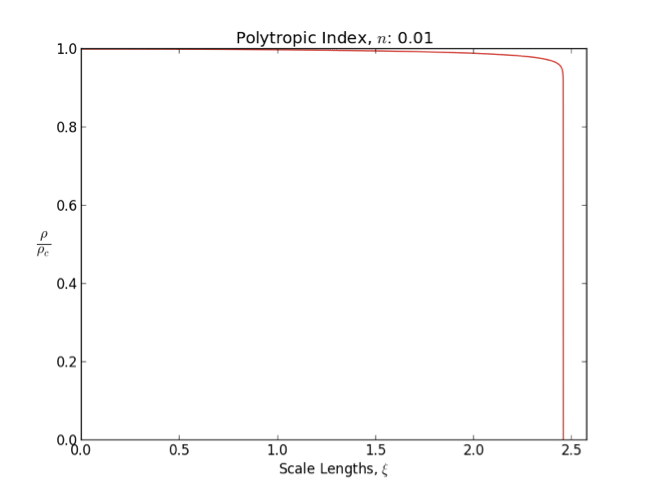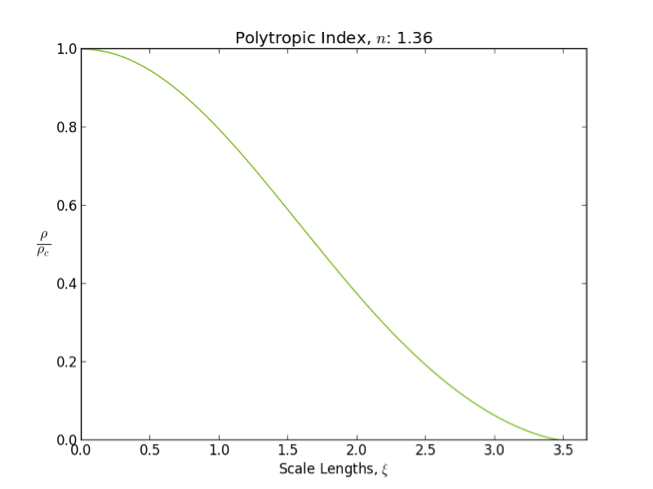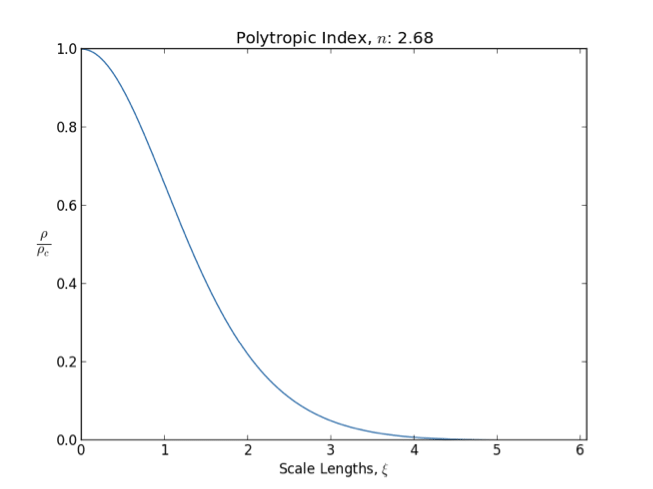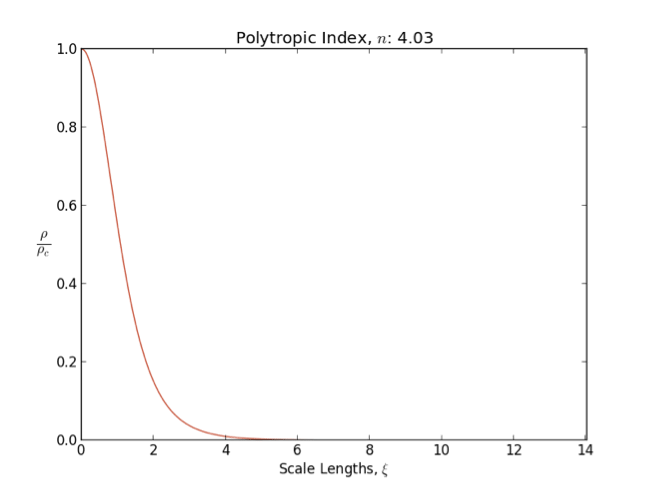
Polytrope
In astrophysics, a polytrope refers to a solution of the Lane–Emden equation in which the pressure depends upon the density in the form P = K \rho^ = K \rho^, where is pressure, is density and is a Constant (mathematics), constant of Proportionality (mathematics), proportionality. The constant is known as the polytropic index; note however that the polytropic index has an alternative definition as with ''n'' as the exponent. This relation need not be interpreted as an equation of state, which states ''P'' as a function of both ρ and ''T'' (the temperature); however in the particular case described by the polytrope equation there are other additional relations between these three quantities, which together determine the equation. Thus, this is simply a relation that expresses an assumption about the change of pressure with radius in terms of the change of density with radius, yielding a solution to the Lane–Emden equation. Sometimes the word ''polytrope'' may refer t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ideal Gas
An ideal gas is a theoretical gas composed of many randomly moving point particles that are not subject to interparticle interactions. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics. The requirement of zero interaction can often be relaxed if, for example, the interaction is perfectly elastic or regarded as point-like collisions. Under various conditions of temperature and pressure, many real gases behave qualitatively like an ideal gas where the gas molecules (or atoms for monatomic gas) play the role of the ideal particles. Many gases such as nitrogen, oxygen, hydrogen, noble gases, some heavier gases like carbon dioxide and mixtures such as air, can be treated as ideal gases within reasonable tolerances over a considerable parameter range around standard temperature and pressure. Generally, a gas behaves more like an ideal gas at higher temperature and lower ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adiabatic Process
An adiabatic process (''adiabatic'' ) is a type of thermodynamic process that occurs without transferring heat between the thermodynamic system and its Environment (systems), environment. Unlike an isothermal process, an adiabatic process transfers energy to the surroundings only as Work (thermodynamics), work and/or mass flow.. A translation may be founhere. Also a mostly reliabltranslation is to be foundin As a key concept in thermodynamics, the adiabatic process supports the theory that explains the first law of thermodynamics. The opposite term to "adiabatic" is ''diabatic''. Some chemical and physical processes occur too rapidly for energy to enter or leave the system as heat, allowing a convenient "adiabatic approximation".Bailyn, M. (1994), pp. 52–53. For example, the adiabatic flame temperature uses this approximation to calculate the upper limit of fire, flame temperature by assuming combustion loses no heat to its surroundings. In meteorology, adiabatic expansion an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sound Wave
In physics, sound is a vibration that propagates as an acoustic wave through a transmission medium such as a gas, liquid or solid. In human physiology and psychology, sound is the ''reception'' of such waves and their ''perception'' by the brain. Only acoustic waves that have frequencies lying between about 20 Hz and 20 kHz, the audio frequency range, elicit an auditory percept in humans. In air at atmospheric pressure, these represent sound waves with wavelengths of to . Sound waves above 20 kHz are known as ultrasound and are not audible to humans. Sound waves below 20 Hz are known as infrasound. Different animal species have varying hearing ranges, allowing some to even hear ultrasounds. Definition Sound is defined as "(a) Oscillation in pressure, stress, particle displacement, particle velocity, etc., propagated in a medium with internal forces (e.g., elastic or viscous), or the superposition of such propagated oscillation. (b) Auditory sens ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sir James Jeans
Sir James Hopwood Jeans (11 September 1877 – 16 September 1946) was an English physicist, mathematician and an astronomer. He served as a secretary of the Royal Society from 1919 to 1929, and was the president of the Royal Astronomical Society from 1925 to 1927, and won its Gold Medal. Early life Born in Ormskirk, Lancashire, the son of William Tulloch Jeans, a parliamentary correspondent and author. Jeans was educated at Merchant Taylors' School, Wilson's Grammar School, Camberwell and Trinity College, Cambridge. As a gifted student, Jeans was counselled to take an aggressive approach to the Cambridge Mathematical Tripos competition: Career Jeans was elected Fellow of Trinity College in October 1901, and taught at Cambridge, but went to Princeton University in 1904 as a professor of applied mathematics. He returned to Cambridge in 1910. From 1923 to 1944 he was associated with Caltech's Mount Wilson Observatory. He made important contributions in many areas of physics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boltzmann Constant
The Boltzmann constant ( or ) is the proportionality factor that relates the average relative thermal energy of particles in a ideal gas, gas with the thermodynamic temperature of the gas. It occurs in the definitions of the kelvin (K) and the molar gas constant, in Planck's law of black-body radiation and Boltzmann's entropy formula, and is used in calculating Johnson–Nyquist noise, thermal noise in resistors. The Boltzmann constant has Dimensional analysis, dimensions of energy divided by temperature, the same as entropy and heat capacity. It is named after the Austrian scientist Ludwig Boltzmann. As part of the 2019 revision of the SI, the Boltzmann constant is one of the seven "Physical constant, defining constants" that have been defined so as to have exact finite decimal values in SI units. They are used in various combinations to define the seven SI base units. The Boltzmann constant is defined to be exactly joules per kelvin, with the effect of defining the SI unit ke ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gravitational Energy
Gravitational energy or gravitational potential energy is the potential energy an object with mass has due to the gravitational potential of its position in a gravitational field. Mathematically, it is the minimum mechanical work that has to be done against the gravitational force to bring a mass from a chosen reference point (often an "infinite distance" from the mass generating the field) to some other point in the field, which is equal to the change in the kinetic energies of the objects as they fall towards each other. Gravitational potential energy increases when two objects are brought further apart and is converted to kinetic energy as they are allowed to fall towards each other. Formulation For two pairwise interacting point particles, the gravitational potential energy U is the work that an outside agent must do in order to quasi-statically bring the masses together (which is therefore, exactly opposite the work done by the gravitational field on the masses): U = -W_g = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |