|
Polytrope
In astrophysics, a polytrope refers to a solution of the Lane–Emden equation in which the pressure depends upon the density in the form :P = K \rho^, where is pressure, is density and is a constant of proportionality. The constant is known as the polytropic index; note however that the polytropic index has an alternative definition as with ''n'' as the exponent. This relation need not be interpreted as an equation of state, which states ''P'' as a function of both ρ and ''T'' (the temperature); however in the particular case described by the polytrope equation there are other additional relations between these three quantities, which together determine the equation. Thus, this is simply a relation that expresses an assumption about the change of pressure with radius in terms of the change of density with radius, yielding a solution to the Lane–Emden equation. Sometimes the word ''polytrope'' may refer to an equation of state that looks similar to the thermody ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
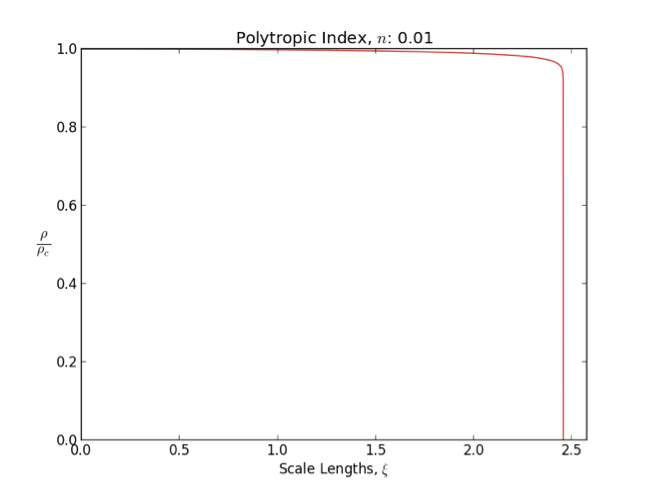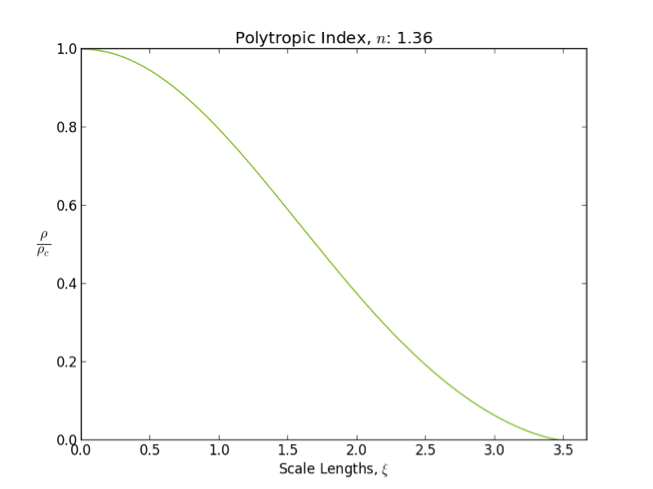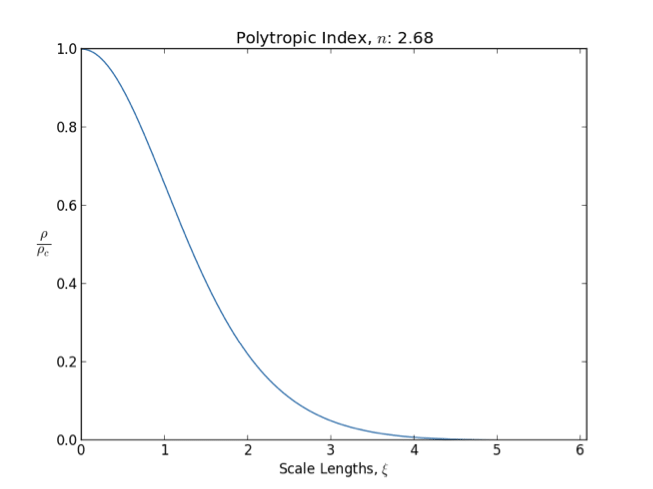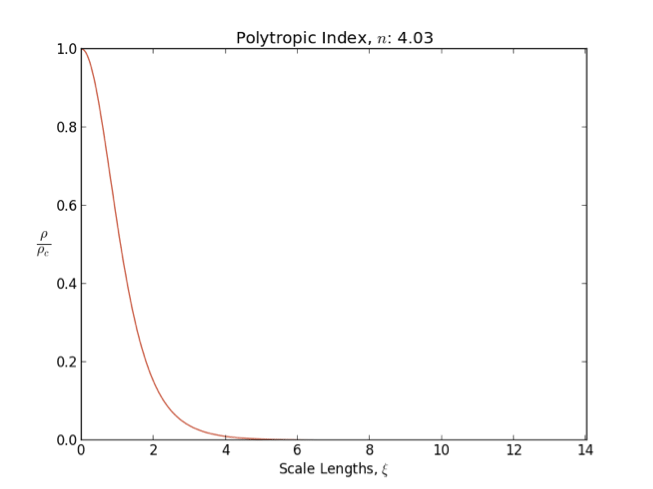
Lane–Emden Equation
In astrophysics, the Lane–Emden equation is a dimensionless form of Poisson's equation for the gravitational potential of a Newtonian self-gravitating, spherically symmetric, polytropic fluid. It is named after astrophysicists Jonathan Homer Lane and Robert Emden. The equation reads : \frac \frac \left(\right) + \theta^n = 0, where \xi is a dimensionless radius and \theta is related to the density, and thus the pressure, by \rho=\rho_c\theta^n for central density \rho_c. The index n is the polytropic index that appears in the polytropic equation of state, : P = K \rho^\, where P and \rho are the pressure and density, respectively, and K is a constant of proportionality. The standard boundary conditions are \theta(0)=1 and \theta'(0)=0. Solutions thus describe the run of pressure and density with radius and are known as ''polytropes'' of index n. If an isothermal fluid (polytropic index tends to infinity) is used instead of a polytropic fluid, one obtains the Emden–Chand ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polytropic Process
A polytropic process is a thermodynamic process that obeys the relation: p V^ = C where ''p'' is the pressure, ''V'' is volume, ''n'' is the polytropic index, and ''C'' is a constant. The polytropic process equation describes expansion and compression processes which include heat transfer. Particular cases Some specific values of ''n'' correspond to particular cases: * n=0 for an isobaric process, * n=+\infty for an isochoric process. In addition, when the ideal gas law applies: * n=1 for an isothermal process, * n=\gamma for an isentropic process. Where \gamma is the ratio of the heat capacity at constant pressure (C_P) to heat capacity at constant volume (C_V). Equivalence between the polytropic coefficient and the ratio of energy transfers For an ideal gas in a closed system undergoing a slow process with negligible changes in kinetic and potential energy the process is polytropic, such that p v^ = C where ''C'' is a constant, K = \frac, \gamma = \frac, and with the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polytropic Index
A polytropic process is a thermodynamic process that obeys the relation: p V^ = C where ''p'' is the pressure, ''V'' is volume, ''n'' is the polytropic index, and ''C'' is a constant. The polytropic process equation describes expansion and compression processes which include heat transfer. Particular cases Some specific values of ''n'' correspond to particular cases: * n=0 for an isobaric process, * n=+\infty for an isochoric process. In addition, when the ideal gas law applies: * n=1 for an isothermal process, * n=\gamma for an isentropic process. Where \gamma is the ratio of the heat capacity at constant pressure (C_P) to heat capacity at constant volume (C_V). Equivalence between the polytropic coefficient and the ratio of energy transfers For an ideal gas in a closed system undergoing a slow process with negligible changes in kinetic and potential energy the process is polytropic, such that p v^ = C where ''C'' is a constant, K = \frac, \gamma = \frac, and with the poly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Murnaghan Equation Of State
The Murnaghan equation of state is a relationship between the volume of a body and the pressure to which it is subjected. This is one of many state equations that have been used in earth sciences and shock physics to model the behavior of matter under conditions of high pressure. It owes its name to Francis D. Murnaghan who proposed it in 1944 to reflect material behavior under a pressure range as wide as possible to reflect an experimentally established fact: the more a solid is compressed, the more difficult it is to compress further. The Murnaghan equation is derived, under certain assumptions, from the equations of continuum mechanics. It involves two adjustable parameters: the modulus of incompressibility ''K''0 and its first derivative with respect to the pressure, ''K''′0, both measured at ambient pressure. In general, these coefficients are determined by a regression on experimentally obtained values of volume ''V'' as a function of the pressure ''P''. These exper ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stellar Core
A stellar core is the extremely hot, dense region at the center of a star. For an ordinary main sequence star, the core region is the volume where the temperature and pressure conditions allow for energy production through thermonuclear fusion of hydrogen into helium. This energy in turn counterbalances the mass of the star pressing inward; a process that self-maintains the conditions in thermal and hydrostatic equilibrium. The minimum temperature required for stellar hydrogen fusion exceeds 107 K (), while the density at the core of the Sun is over . The core is surrounded by the stellar envelope, which transports energy from the core to the stellar atmosphere where it is radiated away into space. Main sequence Main sequence stars are distinguished by the primary energy-generating mechanism in their central region, which joins four hydrogen nuclei to form a single helium atom through thermonuclear fusion. The Sun is an example of this class of stars. Once stars with the mass ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Terrestrial Planet
A terrestrial planet, telluric planet, or rocky planet, is a planet that is composed primarily of silicate rocks or metals. Within the Solar System, the terrestrial planets accepted by the IAU are the inner planets closest to the Sun: Mercury, Venus, Earth and Mars. Among astronomers who use the geophysical definition of a planet, two or three planetary-mass satellites – Earth's Moon, Io, and sometimes Europa – may also be considered terrestrial planets; and so may be the rocky protoplanet-asteroids Pallas and Vesta.Emily Lakdawalla et al.What Is A Planet?The Planetary Society, 21 April 2020 The terms "terrestrial planet" and "telluric planet" are derived from Latin words for Earth (''Terra'' and ''Tellus''), as these planets are, in terms of structure, ''Earth-like''. Terrestrial planets are generally studied by geologists, astronomers, and geophysicists. Terrestrial planets have a solid planetary surface, making them substantially different from the larger gaseous ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neutron Star
A neutron star is the collapsed core of a massive supergiant star, which had a total mass of between 10 and 25 solar masses, possibly more if the star was especially metal-rich. Except for black holes and some hypothetical objects (e.g. white holes, quark stars, and strange stars), neutron stars are the smallest and densest currently known class of stellar objects. Neutron stars have a radius on the order of and a mass of about 1.4 solar masses. They result from the supernova explosion of a massive star, combined with gravitational collapse, that compresses the core past white dwarf star density to that of atomic nuclei. Once formed, they no longer actively generate heat, and cool over time; however, they may still evolve further through collision or accretion. Most of the basic models for these objects imply that neutron stars are composed almost entirely of neutrons (subatomic particles with no net electrical charge and with slightly larger mass than protons); ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Model (abstract)
A conceptual model is a representation of a system. It consists of concepts used to help people know, understand, or simulate a subject the model represents. In contrast, physical models are physical object such as a toy model that may be assembled and made to work like the object it represents. The term may refer to models that are formed after a conceptualization or generalization process. Conceptual models are often abstractions of things in the real world, whether physical or social. Semantic studies are relevant to various stages of concept formation. Semantics is basically about concepts, the meaning that thinking beings give to various elements of their experience. Overview Models of concepts and models that are conceptual The term ''conceptual model'' is normal. It could mean "a model of concept" or it could mean "a model that is conceptual." A distinction can be made between ''what models are'' and ''what models are made of''. With the exception of iconic m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Red Giant
A red giant is a luminous giant star of low or intermediate mass (roughly 0.3–8 solar masses ()) in a late phase of stellar evolution. The outer atmosphere is inflated and tenuous, making the radius large and the surface temperature around or lower. The appearance of the red giant is from yellow-white to reddish-orange, including the spectral types K and M, sometimes G, but also class S stars and most carbon stars. Red giants vary in the way by which they generate energy: * most common red giants are stars on the red-giant branch (RGB) that are still fusing hydrogen into helium in a shell surrounding an inert helium core * red-clump stars in the cool half of the horizontal branch, fusing helium into carbon in their cores via the triple-alpha process * asymptotic-giant-branch (AGB) stars with a helium burning shell outside a degenerate carbon–oxygen core, and a hydrogen-burning shell just beyond that. Many of the well-known bright stars are red giants because they ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Subrahmanyan Chandrasekhar
Subrahmanyan Chandrasekhar (; ) (19 October 1910 – 21 August 1995) was an Indian-American theoretical physicist who spent his professional life in the United States. He shared the 1983 Nobel Prize for Physics with William A. Fowler for "...theoretical studies of the physical processes of importance to the structure and evolution of the stars". His mathematical treatment of stellar evolution yielded many of the current theoretical models of the later evolutionary stages of massive stars and black holes. Many concepts, institutions, and inventions, including the Chandrasekhar limit and the Chandra X-Ray Observatory, are named after him. Chandrasekhar worked on a wide variety of problems in physics during his lifetime, contributing to the contemporary understanding of stellar structure, white dwarfs, stellar dynamics, stochastic process, radiative transfer, the quantum theory of the hydrogen anion, hydrodynamic and hydromagnetic stability, turbulence, equilibrium and the st ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Virginia Louise Trimble
Virginia Louise Trimble (born 1943) is an American astronomer specializing in the structure and evolution of stars and galaxies, and the history of astronomy. She has published more than 600 works in Astrophysics, and dozens of other works in the history of other sciences. She is famous for an annual review of astronomy and astrophysics research that was published in the Publications of the Astronomical Society of the Pacific, and often gives summary reviews at astrophysical conferences. In 2018, she was elected a Patron of the American Astronomical Society, for her many years of intellectual, organizational, and financial contributions to the society. Life Trimble "grew up the only child of a chemist father and a mother with a flair for language, within easy driving distance of both UCLA and Caltech." While attending UCLA in 1962, she was the subject of a ''Life'' article titled "Behind a Lovely Face, a 180 I.Q." The following year, she was selected to promote ''The Twilig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |





.jpg)