|
Invariant Manifold
In dynamical systems, a branch of mathematics, an invariant manifold is a topological manifold that is invariant under the action of the dynamical system. Examples include the slow manifold, center manifold, stable manifold, stable manifold, unstable manifold, subcenter manifold and inertial manifold. Typically, although by no means always, invariant manifolds are constructed as a 'perturbation' of an invariant subspace about an equilibrium. In dissipative systems, an invariant manifold based upon the gravest, longest lasting modes forms an effective low-dimensional, reduced, model of the dynamics. Definition Consider the differential equation dx/dt = f(x),\ x \in \mathbb R^n, with flow x(t)=\phi_t(x_0) being the solution of the differential equation with x(0)=x_0. A set S \subset \mathbb R^n is called an ''invariant set'' for the differential equation if, for each x_0 \in S, the solution t \mapsto \phi_t(x_0), defined on its maximal interval of existence, has its image in S. Alt ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
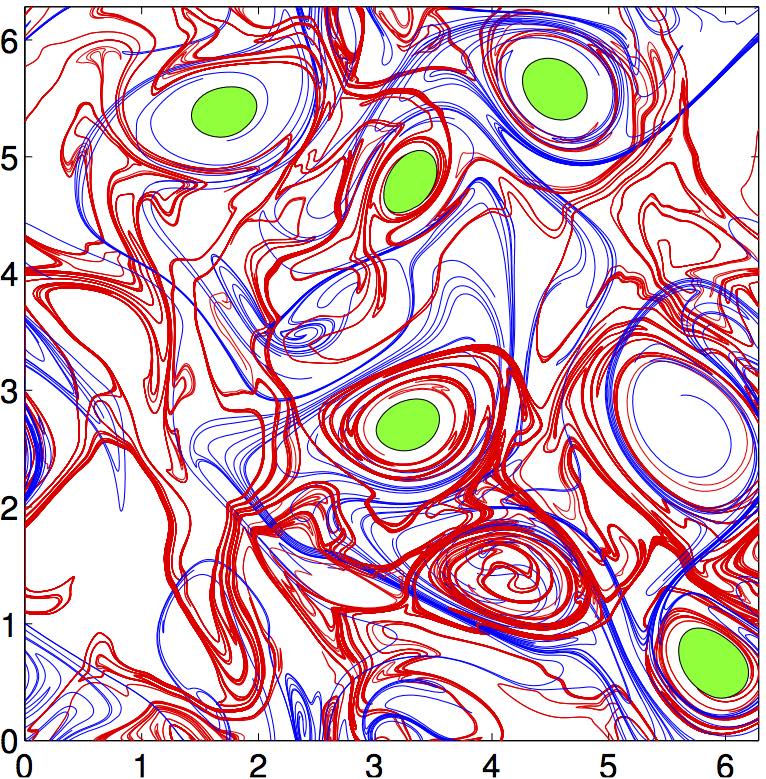
Lagrangian Coherent Structure
Lagrangian coherent structures (LCSs) are distinguished surfaces of trajectories in a dynamical system that exert a major influence on nearby trajectories over a time interval of interest. The type of this influence may vary, but it invariably creates a coherent trajectory pattern for which the underlying LCS serves as a theoretical centerpiece. In observations of tracer patterns in nature, one readily identifies coherent features, but it is often the underlying structure creating these features that is of interest. As illustrated on the right, individual tracer trajectories forming coherent patterns are generally sensitive with respect to changes in their initial conditions and the system parameters. In contrast, the LCSs creating these trajectory patterns turn out to be robust and provide a simplified skeleton of the overall dynamics of the system. The robustness of this skeleton makes LCSs ideal tools for model validation, model comparison and benchmarking. LCSs can also be use ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lagrangian Coherent Structure
Lagrangian coherent structures (LCSs) are distinguished surfaces of trajectories in a dynamical system that exert a major influence on nearby trajectories over a time interval of interest. The type of this influence may vary, but it invariably creates a coherent trajectory pattern for which the underlying LCS serves as a theoretical centerpiece. In observations of tracer patterns in nature, one readily identifies coherent features, but it is often the underlying structure creating these features that is of interest. As illustrated on the right, individual tracer trajectories forming coherent patterns are generally sensitive with respect to changes in their initial conditions and the system parameters. In contrast, the LCSs creating these trajectory patterns turn out to be robust and provide a simplified skeleton of the overall dynamics of the system. The robustness of this skeleton makes LCSs ideal tools for model validation, model comparison and benchmarking. LCSs can also be used ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamical Systems
In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, the random motion of particles in the air, and the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a set, without the need of a smooth space-time structure defined on it. At any given time, a dynamical system has a state representing a point in an appropriate state space. This state is often given by a tuple of real numbers or by a vector in a geometrical manif ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topological Manifold
In topology, a branch of mathematics, a topological manifold is a topological space that locally resembles real ''n''-dimensional Euclidean space. Topological manifolds are an important class of topological spaces, with applications throughout mathematics. All manifolds are topological manifolds by definition. Other types of manifolds are formed by adding structure to a topological manifold (e.g. differentiable manifolds are topological manifolds equipped with a differential structure). Every manifold has an "underlying" topological manifold, obtained by simply "forgetting" the added structure. However, not every topological manifold can be endowed with a particular additional structure. For example, the E8 manifold is a topological manifold which cannot be endowed with a differentiable structure. Formal definition A topological space ''X'' is called locally Euclidean if there is a non-negative integer ''n'' such that every point in ''X'' has a neighborhood which is homeomorphi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Slow Manifold
In mathematics, the slow manifold of an equilibrium point of a dynamical system occurs as the most common example of a center manifold. One of the main methods of simplifying dynamical systems, is to reduce the dimension of the system to that of the slow manifold— center manifold theory rigorously justifies the modelling. For example, some global and regional models of the atmosphere or oceans resolve the so-called quasi-geostrophic flow dynamics on the slow manifold of the atmosphere/oceanic dynamics, and is thus crucial to forecasting with a climate model. In some cases, a slow manifold is defined to be the invariant manifold on which the dynamics are slow compared to the dynamics off the manifold. The slow manifold in a particular problem would be a sub-manifold of either the stable, unstable, or center manifold, exclusively, that has the same dimension of, and is tangent to, the eigenspace with an associated eigenvalue (or eigenvalue pair) that has the smallest real pa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Center Manifold
In the mathematics of evolving systems, the concept of a center manifold was originally developed to determine stability of degenerate equilibria. Subsequently, the concept of center manifolds was realised to be fundamental to mathematical modelling. Center manifolds play an important role in bifurcation theory because interesting behavior takes place on the center manifold and in multiscale mathematics because the long time dynamics of the micro-scale often are attracted to a relatively simple center manifold involving the coarse scale variables. Informal example Saturn's rings provide a rough example of the center manifold of the tidal forces acting on particles within the rings. Tidal forces have a characteristic "compress and stretch" action on bodies, with the compressing direction defining the stable manifold, the stretching direction defining the unstable manifold, and the neutral direction being the center manifold. In the case of Saturn, a particle in orbit above or bel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stable Manifold
In mathematics, and in particular the study of dynamical systems, the idea of ''stable and unstable sets'' or stable and unstable manifolds give a formal mathematical definition to the general notions embodied in the idea of an attractor or repellor. In the case of hyperbolic dynamics, the corresponding notion is that of the hyperbolic set. Physical example The gravitational tidal forces acting on the rings of Saturn provide an easy-to-visualize physical example. The tidal forces flatten the ring into the equatorial plane, even as they stretch it out in the radial direction. Imagining the rings to be sand or gravel particles ("dust") in orbit around Saturn, the tidal forces are such that any perturbations that push particles above or below the equatorial plane results in that particle feeling a restoring force, pushing it back into the plane. Particles effectively oscillate in a harmonic well, damped by collisions. The stable direction is perpendicular to the ring. The unstable di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inertial Manifold
In mathematics, inertial manifolds are concerned with the long term behavior of the solutions of dissipative dynamical systems. Inertial manifolds are finite-dimensional, smooth, invariant manifolds that contain the global attractor and attract all solutions exponential growth, exponentially quickly. Since an inertial manifold is Dimension (vector space), finite-dimensional even if the original system is infinite-dimensional, and because most of the dynamics for the system takes place on the inertial manifold, studying the dynamics on an inertial manifold produces a considerable simplification in the study of the dynamics of the original system.R. Temam. Inertial manifolds. ''Mathematical Intelligencer'', 12:68–74, 1990 In many physical applications, inertial manifolds express an interaction law between the small and large wavelength structures. Some say that the small wavelengths are enslaved by the large (e.g. Synergetics (Haken), synergetics). Inertial manifolds may also ap ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Invariant Subspace
In mathematics, an invariant subspace of a linear mapping ''T'' : ''V'' → ''V '' i.e. from some vector space ''V'' to itself, is a subspace ''W'' of ''V'' that is preserved by ''T''; that is, ''T''(''W'') ⊆ ''W''. General description Consider a linear mapping T :T: W \to W. An invariant subspace W of T has the property that all vectors \mathbf \in W are transformed by T into vectors also contained in W. This can be stated as :\mathbf \in W \implies T(\mathbf) \in W. Trivial examples of invariant subspaces * \mathbb^n: Since T maps every vector in \mathbb^n into \mathbb^n. * \: Since a linear map has to map 0 \mapsto 0. 1-dimensional invariant subspace ''U'' A basis of a 1-dimensional space is simply a non-zero vector \mathbf. Consequently, any vector \mathbf \in U can be represented as \lambda \mathbf where \lambda is a scalar. If we represent T by a matrix A then, for U to be an invariant subspace it must satisfy : \forall \mathbf \in U \; \exists \alpha \in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Equation
In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, and the differential equation defines a relationship between the two. Such relations are common; therefore, differential equations play a prominent role in many disciplines including engineering, physics, economics, and biology. Mainly the study of differential equations consists of the study of their solutions (the set of functions that satisfy each equation), and of the properties of their solutions. Only the simplest differential equations are solvable by explicit formulas; however, many properties of solutions of a given differential equation may be determined without computing them exactly. Often when a closed-form expression for the solutions is not available, solutions may be approximated numerically using computers. The theory of d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |