|
Interpreting Statistical Data
Statistical inference is the process of using data analysis to infer properties of an underlying distribution of probability.Upton, G., Cook, I. (2008) ''Oxford Dictionary of Statistics'', OUP. . Inferential statistical analysis infers properties of a population, for example by testing hypotheses and deriving estimates. It is assumed that the observed data set is sampled from a larger population. Inferential statistics can be contrasted with descriptive statistics. Descriptive statistics is solely concerned with properties of the observed data, and it does not rest on the assumption that the data come from a larger population. In machine learning, the term ''inference'' is sometimes used instead to mean "make a prediction, by evaluating an already trained model"; in this context inferring properties of the model is referred to as ''training'' or ''learning'' (rather than ''inference''), and using a model for prediction is referred to as ''inference'' (instead of ''prediction''); ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Data Analysis
Data analysis is a process of inspecting, cleansing, transforming, and modeling data with the goal of discovering useful information, informing conclusions, and supporting decision-making. Data analysis has multiple facets and approaches, encompassing diverse techniques under a variety of names, and is used in different business, science, and social science domains. In today's business world, data analysis plays a role in making decisions more scientific and helping businesses operate more effectively. Data mining is a particular data analysis technique that focuses on statistical modeling and knowledge discovery for predictive rather than purely descriptive purposes, while business intelligence covers data analysis that relies heavily on aggregation, focusing mainly on business information. In statistical applications, data analysis can be divided into descriptive statistics, exploratory data analysis (EDA), and confirmatory data analysis (CDA). EDA focuses on discoverin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Credible Intervals
In Bayesian statistics, a credible interval is an interval within which an unobserved parameter value falls with a particular probability. It is an interval in the domain of a posterior probability distribution or a predictive distribution. The generalisation to multivariate problems is the credible region. Credible intervals are analogous to confidence intervals and confidence regions in frequentist statistics, although they differ on a philosophical basis: Bayesian intervals treat their bounds as fixed and the estimated parameter as a random variable, whereas frequentist confidence intervals treat their bounds as random variables and the parameter as a fixed value. Also, Bayesian credible intervals use (and indeed, require) knowledge of the situation-specific prior distribution, while the frequentist confidence intervals do not. For example, in an experiment that determines the distribution of possible values of the parameter \mu, if the subjective probability that \mu lies ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
David A
David (; , "beloved one") (traditional spelling), , ''Dāwūd''; grc-koi, Δαυΐδ, Dauíd; la, Davidus, David; gez , ዳዊት, ''Dawit''; xcl, Դաւիթ, ''Dawitʿ''; cu, Давíдъ, ''Davidŭ''; possibly meaning "beloved one". was, according to the Hebrew Bible, the third king of the United Kingdom of Israel. In the Books of Samuel, he is described as a young shepherd and harpist who gains fame by slaying Goliath, a champion of the Philistines, in southern Canaan. David becomes a favourite of Saul, the first king of Israel; he also forges a notably close friendship with Jonathan, a son of Saul. However, under the paranoia that David is seeking to usurp the throne, Saul attempts to kill David, forcing the latter to go into hiding and effectively operate as a fugitive for several years. After Saul and Jonathan are both killed in battle against the Philistines, a 30-year-old David is anointed king over all of Israel and Judah. Following his rise to power, Dav ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normality Histogram
Normality may refer to: Mathematics, probability, and statistics * Asymptotic normality, in mathematics and statistics * Complete normality or normal space, * Log-normality, in probability theory * Normality (category theory) * Normality (statistics) or normal distribution, in probability theory * Normality tests, used to determine if a data set is well-modeled by a normal distribution Science * Normality (behavior), the property of conforming to a norm * Normality (chemistry), the equivalent concentration of a solution * Principle of normality, in solid mechanics Other uses * ''Normality'' (video game), a 1996 adventure video game by Gremlin Interactive * Normality bias, a belief people hold when considering the possibility of a disaster See also * Normal (other) Normal(s) or The Normal(s) may refer to: Film and television * ''Normal'' (2003 film), starring Jessica Lange and Tom Wilkinson * ''Normal'' (2007 film), starring Carrie-Anne Moss, Kevin Zegers, Callum ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cox Model
Proportional hazards models are a class of survival models in statistics. Survival models relate the time that passes, before some event occurs, to one or more covariates that may be associated with that quantity of time. In a proportional hazards model, the unique effect of a unit increase in a covariate is multiplicative with respect to the hazard rate. For example, taking a drug may halve one's hazard rate for a stroke occurring, or, changing the material from which a manufactured component is constructed may double its hazard rate for failure. Other types of survival models such as accelerated failure time models do not exhibit proportional hazards. The accelerated failure time model describes a situation where the biological or mechanical life history of an event is accelerated (or decelerated). Background Survival models can be viewed as consisting of two parts: the underlying baseline hazard function, often denoted \lambda_0(t), describing how the risk of event per ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
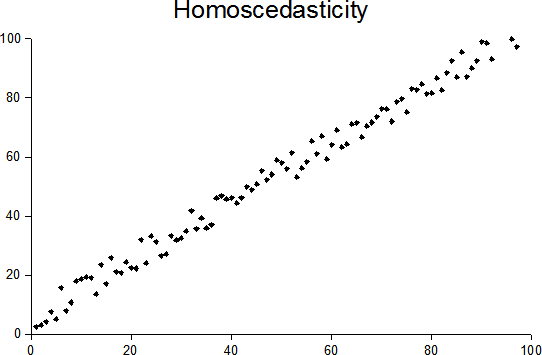
Heteroscedasticity
In statistics, a sequence (or a vector) of random variables is homoscedastic () if all its random variables have the same finite variance. This is also known as homogeneity of variance. The complementary notion is called heteroscedasticity. The spellings ''homoskedasticity'' and ''heteroskedasticity'' are also frequently used. Assuming a variable is homoscedastic when in reality it is heteroscedastic () results in unbiased but inefficient point estimates and in biased estimates of standard errors, and may result in overestimating the goodness of fit as measured by the Pearson coefficient. The existence of heteroscedasticity is a major concern in regression analysis and the analysis of variance, as it invalidates statistical tests of significance that assume that the modelling errors all have the same variance. While the ordinary least squares estimator is still unbiased in the presence of heteroscedasticity, it is inefficient and generalized least squares should be used i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semiparametric Model
In statistics, a semiparametric model is a statistical model that has parametric and nonparametric components. A statistical model is a parameterized family of distributions: \ indexed by a parameter \theta. * A parametric model is a model in which the indexing parameter \theta is a vector in k-dimensional Euclidean space, for some nonnegative integer k.. Thus, \theta is finite-dimensional, and \Theta \subseteq \mathbb^k. * With a nonparametric model, the set of possible values of the parameter \theta is a subset of some space V, which is not necessarily finite-dimensional. For example, we might consider the set of all distributions with mean 0. Such spaces are vector spaces with topological structure, but may not be finite-dimensional as vector spaces. Thus, \Theta \subseteq V for some possibly infinite-dimensional space V. * With a semiparametric model, the parameter has both a finite-dimensional component and an infinite-dimensional component (often a real-valued functio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hodges–Lehmann Estimator
In statistics, the Hodges–Lehmann estimator is a robust and nonparametric estimator of a population's location parameter. For populations that are symmetric about one median, such as the (Gaussian) normal distribution or the Student ''t''-distribution, the Hodges–Lehmann estimator is a consistent and median-unbiased estimate of the population median. For non-symmetric populations, the Hodges–Lehmann estimator estimates the "pseudo–median", which is closely related to the population median. The Hodges–Lehmann estimator was proposed originally for estimating the location parameter of one-dimensional populations, but it has been used for many more purposes. It has been used to estimate the differences between the members of two populations. It has been generalized from univariate populations to multivariate populations, which produce samples of vectors. It is based on the Wilcoxon signed-rank statistic. In statistical theory, it was an early example of a rank-based ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonparametric Statistics
Nonparametric statistics is the branch of statistics that is not based solely on parametrized families of probability distributions (common examples of parameters are the mean and variance). Nonparametric statistics is based on either being distribution-free or having a specified distribution but with the distribution's parameters unspecified. Nonparametric statistics includes both descriptive statistics and statistical inference. Nonparametric tests are often used when the assumptions of parametric tests are violated. Definitions The term "nonparametric statistics" has been imprecisely defined in the following two ways, among others: Applications and purpose Non-parametric methods are widely used for studying populations that take on a ranked order (such as movie reviews receiving one to four stars). The use of non-parametric methods may be necessary when data have a ranking but no clear numerical interpretation, such as when assessing preferences. In terms of levels of me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalized Linear Model
In statistics, a generalized linear model (GLM) is a flexible generalization of ordinary linear regression. The GLM generalizes linear regression by allowing the linear model to be related to the response variable via a ''link function'' and by allowing the magnitude of the variance of each measurement to be a function of its predicted value. Generalized linear models were formulated by John Nelder and Robert Wedderburn as a way of unifying various other statistical models, including linear regression, logistic regression and Poisson regression. They proposed an iteratively reweighted least squares method for maximum likelihood estimation (MLE) of the model parameters. MLE remains popular and is the default method on many statistical computing packages. Other approaches, including Bayesian regression and least squares fitting to variance stabilized responses, have been developed. Intuition Ordinary linear regression predicts the expected value of a given unknown quantity ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simple Random Sample
In statistics, a simple random sample (or SRS) is a subset of individuals (a sample) chosen from a larger set (a population) in which a subset of individuals are chosen randomly, all with the same probability. It is a process of selecting a sample in a random way. In SRS, each subset of ''k'' individuals has the same probability of being chosen for the sample as any other subset of ''k'' individuals. A simple random sample is an unbiased sampling technique. Simple random sampling is a basic type of sampling and can be a component of other more complex sampling methods. Introduction The principle of simple random sampling is that every set of items has the same probability of being chosen. For example, suppose ''N'' college students want to get a ticket for a basketball game, but there are only ''X'' < ''N'' tickets for them, so they decide to have a fair way to see who gets to go. Then, everybody is given a number in the range from 0 to ''N''-1, and random numbers are generate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parametric Model
In statistics, a parametric model or parametric family or finite-dimensional model is a particular class of statistical models. Specifically, a parametric model is a family of probability distributions that has a finite number of parameters. Definition A statistical model is a collection of probability distributions on some sample space. We assume that the collection, , is indexed by some set . The set is called the parameter set or, more commonly, the parameter space. For each , let denote the corresponding member of the collection; so is a cumulative distribution function. Then a statistical model can be written as : \mathcal = \big\. The model is a parametric model if for some positive integer . When the model consists of absolutely continuous distributions, it is often specified in terms of corresponding probability density functions: : \mathcal = \big\. Examples * The Poisson family of distributions is parametrized by a single number : : \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |