|
Internal Pressure
Internal pressure is a measure of how the internal energy of a system changes when it expands or contracts at constant temperature. It has the same dimensions as pressure, the SI unit of which is the pascal. Internal pressure is usually given the symbol \pi_T. It is defined as a partial derivative of internal energy with respect to volume at constant temperature: \pi _T = \left ( \frac \right )_T Thermodynamic equation of state Internal pressure can be expressed in terms of temperature, pressure and their mutual dependence: \pi_T = T \left ( \frac \right )_V - p This equation is one of the simplest thermodynamic equations. More precisely, it is a thermodynamic property relation, since it holds true for any system and connects the equation of state to one or more thermodynamic energy properties. Here we refer to it as a "thermodynamic equation of state." : Perfect gas In a perfect gas, there are no potential energy interactions between the particles, so any change in the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Internal Energy
The internal energy of a thermodynamic system is the total energy contained within it. It is the energy necessary to create or prepare the system in its given internal state, and includes the contributions of potential energy and internal kinetic energy. It keeps account of the gains and losses of energy of the system that are due to changes in its internal state. It does not include the kinetic energy of motion of the system as a whole, or any external energies from surrounding force fields. The internal energy of an isolated system is constant, which is expressed as the law of conservation of energy, a foundation of the first law of thermodynamics. The internal energy is an extensive property. The internal energy cannot be measured directly and knowledge of all its components is rarely interesting, such as the static rest mass energy of its constituent matter. Thermodynamics is chiefly concerned only with ''changes'' in the internal energy, not with its absolute value. Instea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kinetic Energy
In physics, the kinetic energy of an object is the energy that it possesses due to its motion. It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes. The same amount of work is done by the body when decelerating from its current speed to a state of rest. Formally, a kinetic energy is any term in a system's Lagrangian which includes a derivative with respect to time. In classical mechanics, the kinetic energy of a non-rotating object of mass ''m'' traveling at a speed ''v'' is \fracmv^2. In relativistic mechanics, this is a good approximation only when ''v'' is much less than the speed of light. The standard unit of kinetic energy is the joule, while the English unit of kinetic energy is the foot-pound. History and etymology The adjective ''kinetic'' has its roots in the Greek word κίνησις ''kinesis'', m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Water
Water (chemical formula ) is an inorganic, transparent, tasteless, odorless, and nearly colorless chemical substance, which is the main constituent of Earth's hydrosphere and the fluids of all known living organisms (in which it acts as a solvent). It is vital for all known forms of life, despite not providing food, energy or organic micronutrients. Its chemical formula, H2O, indicates that each of its molecules contains one oxygen and two hydrogen atoms, connected by covalent bonds. The hydrogen atoms are attached to the oxygen atom at an angle of 104.45°. "Water" is also the name of the liquid state of H2O at standard temperature and pressure. A number of natural states of water exist. It forms precipitation in the form of rain and aerosols in the form of fog. Clouds consist of suspended droplets of water and ice, its solid state. When finely divided, crystalline ice may precipitate in the form of snow. The gaseous state of water is steam or water vapor. Water co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Specific Heat Capacity
In thermodynamics, the specific heat capacity (symbol ) of a substance is the heat capacity of a sample of the substance divided by the mass of the sample, also sometimes referred to as massic heat capacity. Informally, it is the amount of heat that must be added to one unit of mass of the substance in order to cause an increase of one unit in temperature. The SI unit of specific heat capacity is joule per kelvin per kilogram, J⋅kg−1⋅K−1. For example, the heat required to raise the temperature of of water by is , so the specific heat capacity of water is . Specific heat capacity often varies with temperature, and is different for each state of matter. Liquid water has one of the highest specific heat capacities among common substances, about at 20 °C; but that of ice, just below 0 °C, is only . The specific heat capacities of iron, granite, and hydrogen gas are about 449 J⋅kg−1⋅K−1, 790 J⋅kg−1⋅K−1, and 14300 J⋅kg−1⋅K−1 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
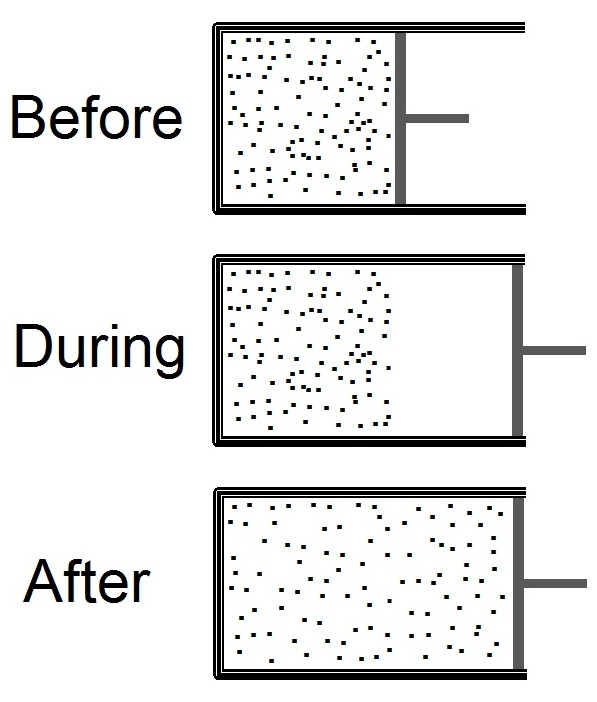
Joule Expansion
The Joule expansion (also called free expansion) is an irreversible process in thermodynamics in which a volume of gas is kept in one side of a thermally isolated container (via a small partition), with the other side of the container being evacuated. The partition between the two parts of the container is then opened, and the gas fills the whole container. The Joule expansion, treated as a thought experiment involving ideal gases, is a useful exercise in classical thermodynamics. It provides a convenient example for calculating changes in thermodynamic quantities, including the resulting increase in entropy of the universe (entropy production) that results from this inherently irreversible process. An actual Joule expansion experiment necessarily involves real gases; the temperature change in such a process provides a measure of intermolecular forces. This type of expansion is named after James Prescott Joule who used this expansion, in 1845, in his study for the mechanical equ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
James Joule
James Prescott Joule (; 24 December 1818 11 October 1889) was an English physicist, mathematician and brewer, born in Salford, Lancashire. Joule studied the nature of heat, and discovered its relationship to mechanical work (see energy). This led to the law of conservation of energy, which in turn led to the development of the first law of thermodynamics. The SI derived unit of energy, the joule, is named after him. He worked with Lord Kelvin to develop an absolute thermodynamic temperature scale, which came to be called the Kelvin scale. Joule also made observations of magnetostriction, and he found the relationship between the current through a resistor and the heat dissipated, which is also called Joule's first law. His experiments about energy transformations were first published in 1843. Early years James Joule was born in 1818, the son of Benjamin Joule (1784–1858), a wealthy brewer, and his wife, Alice Prescott, on New Bailey Street in Salford. Joule was tu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compression Factor
In thermodynamics, the compressibility factor (Z), also known as the compression factor or the gas deviation factor, describes the deviation of a real gas from ideal gas behaviour. It is simply defined as the ratio of the molar volume of a gas to the molar volume of an ideal gas at the same temperature and pressure. It is a useful thermodynamic property for modifying the ideal gas law to account for the real gas behaviour.Properties of Natural Gases . Includes a chart of compressibility factors versus reduced pressure and reduced temperature (on last page of the PDF document) In general, deviation from ideal behaviour becomes more significant the closer a gas is to a |
Van Der Waals Equation
In chemistry and thermodynamics, the Van der Waals equation (or Van der Waals equation of state) is an equation of state which extends the ideal gas law to include the effects of interaction between molecules of a gas, as well as accounting for the finite size of the molecules. The ideal gas law treats gas molecules as point particles that interact with their containers but not each other, meaning they neither take up space nor change kinetic energy during collisions (i.e. all collisions are perfectly elastic). The ideal gas law states that the volume ''V'' occupied by ''n'' moles of any gas has a pressure ''P'' at temperature ''T'' given by the following relationship, where ''R'' is the gas constant: :PV=nRT To account for the volume occupied by real gas molecules, the Van der Waals equation replaces V/n in the ideal gas law with (V_m-b), where ''Vm'' is the molar volume of the gas and ''b'' is the volume occupied by the molecules of one mole: :P(V_m - b)=R T The second m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Internal Pressure Gases
{{disambig ...
Internal may refer to: *Internality as a concept in behavioural economics *Neijia, internal styles of Chinese martial arts *Neigong or "internal skills", a type of exercise in meditation associated with Daoism *''Internal (album)'' by Safia, 2016 See also * *Internals (other) *External (other) External may refer to: * External (mathematics), a concept in abstract algebra * Externality In economics, an externality or external cost is an indirect cost or benefit to an uninvolved third party that arises as an effect of another party' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ideal Gas Law
The ideal gas law, also called the general gas equation, is the equation of state of a hypothetical ideal gas. It is a good approximation of the behavior of many gases under many conditions, although it has several limitations. It was first stated by Benoît Paul Émile Clapeyron in 1834 as a combination of the empirical Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law. The ideal gas law is often written in an empirical form: pV = nRT where p, V and T are the pressure, volume and temperature; n is the amount of substance; and R is the ideal gas constant. It can also be derived from the microscopic kinetic theory, as was achieved (apparently independently) by August Krönig in 1856 and Rudolf Clausius in 1857. Equation The state of an amount of gas is determined by its pressure, volume, and temperature. The modern form of the equation relates these simply in two main forms. The temperature used in the equation of state is an absolute temperature: the appropria ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Potential Energy
In physics, potential energy is the energy held by an object because of its position relative to other objects, stresses within itself, its electric charge, or other factors. Common types of potential energy include the gravitational potential energy of an object, the elastic potential energy of an extended spring, and the electric potential energy of an electric charge in an electric field. The unit for energy in the International System of Units (SI) is the joule, which has the symbol J. The term ''potential energy'' was introduced by the 19th-century Scottish engineer and physicist William Rankine, although it has links to Greek philosopher Aristotle's concept of potentiality. Potential energy is associated with forces that act on a body in a way that the total work done by these forces on the body depends only on the initial and final positions of the body in space. These forces, that are called ''conservative forces'', can be represented at every point in space by vec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |