|
Infinitesimal Generator (stochastic Processes)
In mathematics — specifically, in stochastic analysis — the infinitesimal generator of a Feller process (i.e. a continuous-time Markov process satisfying certain regularity conditions) is a Fourier multiplier operator that encodes a great deal of information about the process. The generator is used in evolution equations such as the Kolmogorov backward equation (which describes the evolution of statistics of the process); its ''L''2 Hermitian adjoint is used in evolution equations such as the Fokker–Planck equation (which describes the evolution of the probability density functions of the process). Definition General case For a Feller process (X_t)_ with Feller semigroup T=(T_t)_ and state space E we define the generator (A,D(A)) by :D(A)=\left\, :A f=\lim_ \frac, for any f\in D(A). Here C_(E) denotes the Banach space of continuous functions on E vanishing at infinity, equipped with the supremum norm, and T_t f(x)= \mathbb^x f(X_t)=\mathbb(f(X_t), X_0=x). In ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Stochastic Processes
In probability theory and related fields, a stochastic () or random process is a mathematical object usually defined as a family of random variables. Stochastic processes are widely used as mathematical models of systems and phenomena that appear to vary in a random manner. Examples include the growth of a bacterial population, an electrical current fluctuating due to thermal noise, or the movement of a gas molecule. Stochastic processes have applications in many disciplines such as biology, chemistry, ecology, neuroscience, physics, image processing, signal processing, control theory, information theory, computer science, cryptography and telecommunications. Furthermore, seemingly random changes in financial markets have motivated the extensive use of stochastic processes in finance. Applications and the study of phenomena have in turn inspired the proposal of new stochastic processes. Examples of such stochastic processes include the Wiener process or Browni ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Feller Process
In probability theory relating to stochastic processes, a Feller process is a particular kind of Markov process. Definitions Let ''X'' be a locally compact Hausdorff space with a countable base. Let ''C''0(''X'') denote the space of all real-valued continuous functions on ''X'' that vanish at infinity, equipped with the sup-norm , , ''f'' , , . From analysis, we know that ''C''0(''X'') with the sup norm is a Banach space. A Feller semigroup on ''C''0(''X'') is a collection ''t'' ≥ 0 of positive linear maps from ''C''0(''X'') to itself such that * , , ''T''''t''''f'' , , ≤ , , ''f'' , , for all ''t'' ≥ 0 and ''f'' in ''C''0(''X''), i.e., it is a contraction (in the weak sense); * the semigroup property: ''T''''t'' + ''s'' = ''T''''t'' o''T''''s'' for all ''s'', ''t'' ≥ 0; * lim''t'' → 0, , ''T''''t''''f'' − ''f'' , , = 0 for every ''f'' in ''C''0(''X''). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Multiplier (Fourier Analysis)
In Fourier analysis, a multiplier operator is a type of linear operator, or transformation of functions. These operators act on a function by altering its Fourier transform. Specifically they multiply the Fourier transform of a function by a specified function known as the multiplier or symbol. Occasionally, the term ''multiplier operator'' itself is shortened simply to ''multiplier''. In simple terms, the multiplier reshapes the frequencies involved in any function. This class of operators turns out to be broad: general theory shows that a translation-invariant operator on a group which obeys some (very mild) regularity conditions can be expressed as a multiplier operator, and conversely. Many familiar operators, such as translations and differentiation, are multiplier operators, although there are many more complicated examples such as the Hilbert transform. In signal processing, a multiplier operator is called a "filter", and the multiplier is the filter's frequency response ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Kolmogorov Backward Equation
In probability theory, Kolmogorov equations, including Kolmogorov forward equations and Kolmogorov backward equations, characterize continuous-time Markov processes. In particular, they describe how the probability that a continuous-time Markov process is in a certain state changes over time. Diffusion processes vs. jump processes Writing in 1931, Andrei Kolmogorov started from the theory of discrete time Markov processes, which are described by the Chapman–Kolmogorov equation, and sought to derive a theory of continuous time Markov processes by extending this equation. He found that there are two kinds of continuous time Markov processes, depending on the assumed behavior over small intervals of time: If you assume that "in a small time interval there is an overwhelming probability that the state will remain unchanged; however, if it changes, the change may be radical", then you are led to what are called jump processes. The other case leads to processes such as those "repre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Lp Space
In mathematics, the spaces are function spaces defined using a natural generalization of the -norm for finite-dimensional vector spaces. They are sometimes called Lebesgue spaces, named after Henri Lebesgue , although according to the Bourbaki group they were first introduced by Frigyes Riesz . spaces form an important class of Banach spaces in functional analysis, and of topological vector spaces. Because of their key role in the mathematical analysis of measure and probability spaces, Lebesgue spaces are used also in the theoretical discussion of problems in physics, statistics, economics, finance, engineering, and other disciplines. Applications Statistics In statistics, measures of central tendency and statistical dispersion, such as the mean, median, and standard deviation, are defined in terms of metrics, and measures of central tendency can be characterized as solutions to variational problems. In penalized regression, "L1 penalty" and "L2 penalty" refer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Hermitian Adjoint
In mathematics, specifically in operator theory, each linear operator A on a Euclidean vector space defines a Hermitian adjoint (or adjoint) operator A^* on that space according to the rule :\langle Ax,y \rangle = \langle x,A^*y \rangle, where \langle \cdot,\cdot \rangle is the inner product on the vector space. The adjoint may also be called the Hermitian conjugate or simply the Hermitian after Charles Hermite. It is often denoted by in fields like physics, especially when used in conjunction with bra–ket notation in quantum mechanics. In finite dimensions where operators are represented by matrices, the Hermitian adjoint is given by the conjugate transpose (also known as the Hermitian transpose). The above definition of an adjoint operator extends verbatim to bounded linear operators on Hilbert spaces H. The definition has been further extended to include unbounded ''densely defined'' operators whose domain is topologically dense in—but not necessarily equal to� ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
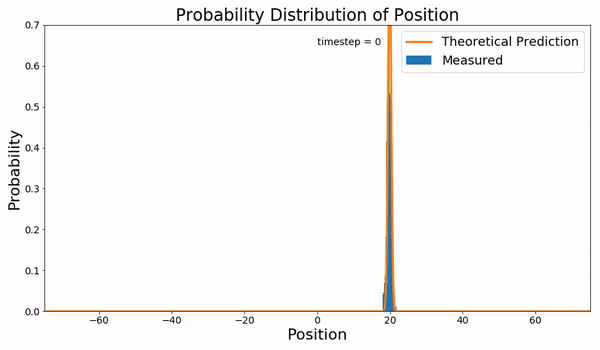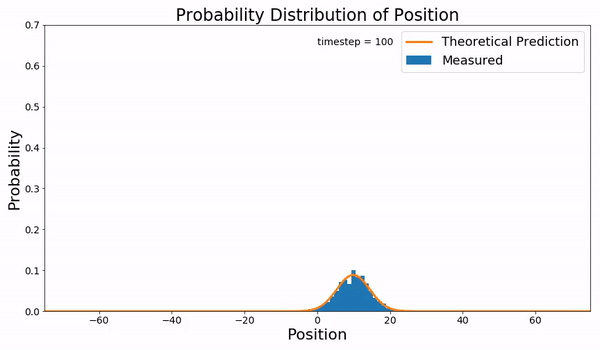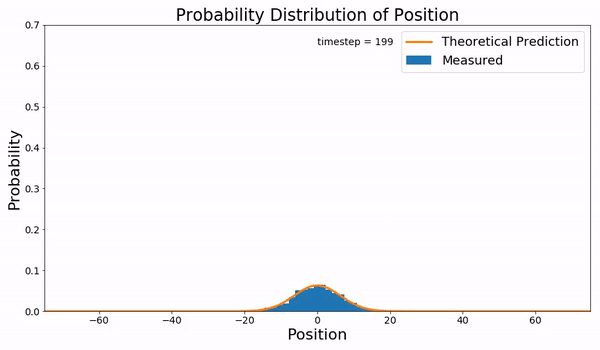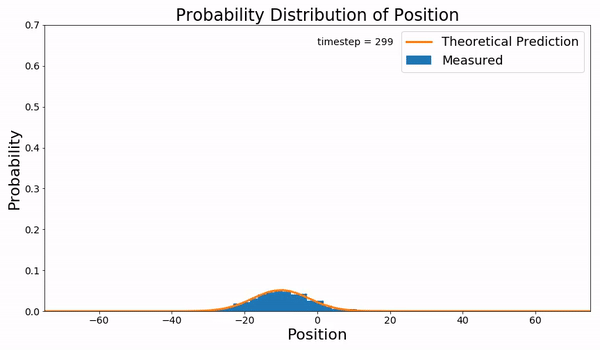 |
Fokker–Planck Equation
In statistical mechanics, the Fokker–Planck equation is a partial differential equation that describes the time evolution of the probability density function of the velocity of a particle under the influence of drag forces and random forces, as in Brownian motion. The equation can be generalized to other observables as well. It is named after Adriaan Fokker and Max Planck, who described it in 1914 and 1917. It is also known as the Kolmogorov forward equation, after Andrey Kolmogorov, who independently discovered it in 1931. When applied to particle position distributions, it is better known as the Smoluchowski equation (after Marian Smoluchowski), and in this context it is equivalent to the convection–diffusion equation. The case with zero diffusion is the continuity equation. The Fokker–Planck equation is obtained from the master equation through Kramers–Moyal expansion. The first consistent microscopic derivation of the Fokker–Planck equation in the single ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Probability Density Function
In probability theory, a probability density function (PDF), or density of a continuous random variable, is a function whose value at any given sample (or point) in the sample space (the set of possible values taken by the random variable) can be interpreted as providing a ''relative likelihood'' that the value of the random variable would be close to that sample. Probability density is the probability per unit length, in other words, while the ''absolute likelihood'' for a continuous random variable to take on any particular value is 0 (since there is an infinite set of possible values to begin with), the value of the PDF at two different samples can be used to infer, in any particular draw of the random variable, how much more likely it is that the random variable would be close to one sample compared to the other sample. In a more precise sense, the PDF is used to specify the probability of the random variable falling ''within a particular range of values'', as opposed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Test Functions
Distributions, also known as Schwartz distributions or generalized functions, are objects that generalize the classical notion of functions in mathematical analysis. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative. Distributions are widely used in the theory of partial differential equations, where it may be easier to establish the existence of distributional solutions than classical solutions, or where appropriate classical solutions may not exist. Distributions are also important in physics and engineering where many problems naturally lead to differential equations whose solutions or initial conditions are singular, such as the Dirac delta function. A function f is normally thought of as on the in the function domain by "sending" a point x in its domain to the point f(x). Instead of acting on points, distribution theory reinterpr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Lévy Process
In probability theory, a Lévy process, named after the French mathematician Paul Lévy, is a stochastic process with independent, stationary increments: it represents the motion of a point whose successive displacements are random, in which displacements in pairwise disjoint time intervals are independent, and displacements in different time intervals of the same length have identical probability distributions. A Lévy process may thus be viewed as the continuous-time analog of a random walk. The most well known examples of Lévy processes are the Wiener process, often called the Brownian motion process, and the Poisson process. Further important examples include the Gamma process, the Pascal process, and the Meixner process. Aside from Brownian motion with drift, all other proper (that is, not deterministic) Lévy processes have discontinuous paths. All Lévy processes are additive processes. Mathematical definition A stochastic process X=\ is said to be a Lévy process ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Transition Rate Matrix
Transition or transitional may refer to: Mathematics, science, and technology Biology * Transition (genetics), a point mutation that changes a purine nucleotide to another purine (A ↔ G) or a pyrimidine nucleotide to another pyrimidine (C ↔ T) * Transitional fossil, any fossilized remains of a lifeform that exhibits the characteristics of two distinct taxonomic groups * A phase during childbirth contractions during which the cervix completes its dilation Gender and sex * Gender transitioning, the process of changing one's gender presentation to accord with one's internal sense of one's gender – the idea of what it means to be a man or woman * Sex reassignment therapy, the physical aspect of a gender transition Physics * Phase transition, a transformation of the state of matter; for example, the change between a solid and a liquid, between liquid and gas or between gas and plasma * Quantum phase transition, a phase transformation between different quantum phases * Quantum ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |