|
Index Notation
In mathematics and computer programming, index notation is used to specify the elements of an array of numbers. The formalism of how indices are used varies according to the subject. In particular, there are different methods for referring to the elements of a list, a vector, or a matrix, depending on whether one is writing a formal mathematical paper for publication, or when one is writing a computer program. In mathematics It is frequently helpful in mathematics to refer to the elements of an array using subscripts. The subscripts can be integers or variables. The array takes the form of tensors in general, since these can be treated as multi-dimensional arrays. Special (and more familiar) cases are vectors (1d arrays) and matrices (2d arrays). The following is only an introduction to the concept: index notation is used in more detail in mathematics (particularly in the representation and manipulation of tensor operations). See the main article for further details. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vectors In Mathematics And Physics
In mathematics and physics, vector is a term that refers to quantities that cannot be expressed by a single number (a scalar), or to elements of some vector spaces. Historically, vectors were introduced in geometry and physics (typically in mechanics) for quantities that have both a magnitude and a direction, such as displacements, forces and velocity. Such quantities are represented by geometric vectors in the same way as distances, masses and time are represented by real numbers. The term ''vector'' is also used, in some contexts, for tuples, which are finite sequences (of numbers or other objects) of a fixed length. Both geometric vectors and tuples can be added and scaled, and these vector operations led to the concept of a vector space, which is a set equipped with a vector addition and a scalar multiplication that satisfy some axioms generalizing the main properties of operations on the above sorts of vectors. A vector space formed by geometric vectors is called a Euc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
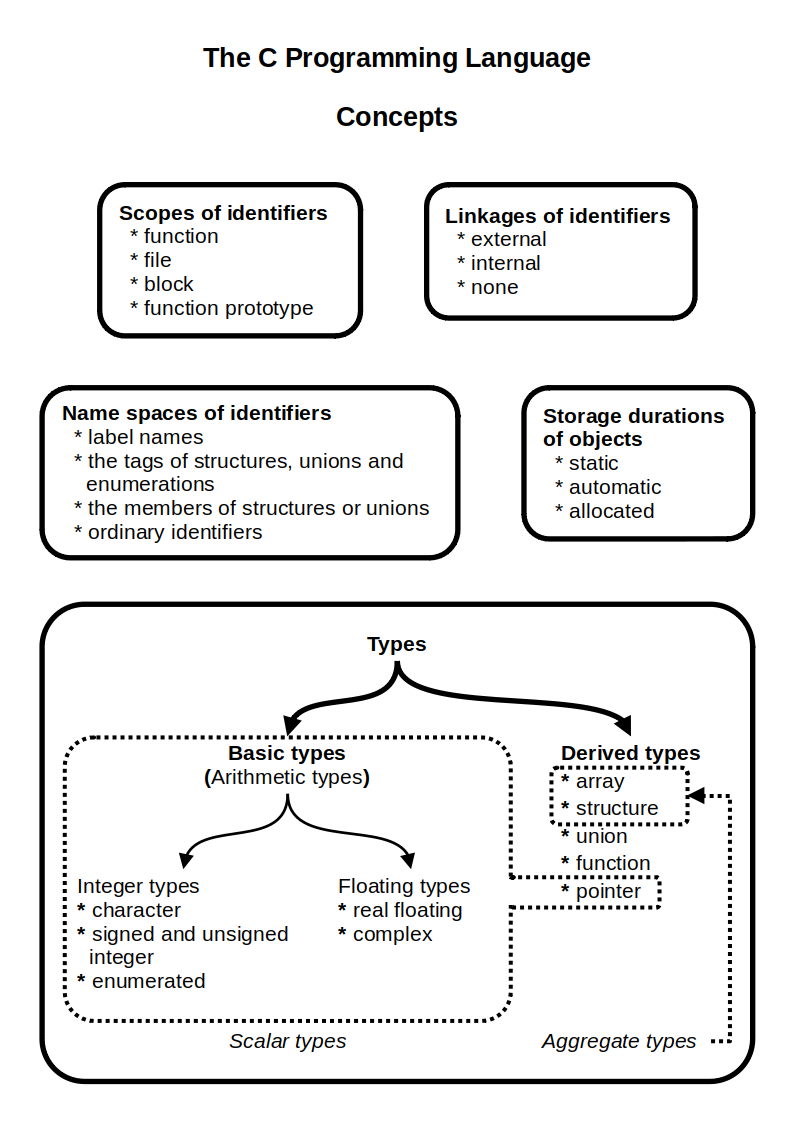
C (programming Language)
C (''pronounced'' '' – like the letter c'') is a general-purpose programming language. It was created in the 1970s by Dennis Ritchie and remains very widely used and influential. By design, C's features cleanly reflect the capabilities of the targeted Central processing unit, CPUs. It has found lasting use in operating systems code (especially in Kernel (operating system), kernels), device drivers, and protocol stacks, but its use in application software has been decreasing. C is commonly used on computer architectures that range from the largest supercomputers to the smallest microcontrollers and embedded systems. A successor to the programming language B (programming language), B, C was originally developed at Bell Labs by Ritchie between 1972 and 1973 to construct utilities running on Unix. It was applied to re-implementing the kernel of the Unix operating system. During the 1980s, C gradually gained popularity. It has become one of the most widely used programming langu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zero-based Numbering
Zero-based numbering is a way of numbering in which the initial element of a sequence is assigned the index 0, rather than the index 1 as is typical in everyday non-mathematical or non-programming circumstances. Under zero-based numbering, the initial element is sometimes termed the '' zeroth'' element, rather than the ''first'' element; ''zeroth'' is a coined word for the ordinal number zero. In some cases, an object or value that does not (originally) belong to a given sequence, but which could be naturally placed before its initial element, may be termed the zeroth element. There is no wide agreement regarding the correctness of using zero as an ordinal (nor regarding the use of the term ''zeroth''), as it creates ambiguity for all subsequent elements of the sequence when lacking context. Numbering sequences starting at 0 is quite common in mathematics notation, in particular in combinatorics, though programming languages for mathematics usually index from 1. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Base Address
In computing, a base address is an address serving as a reference point ("base") for other addresses. Related addresses can be accessed using an ''addressing scheme''. Under the ''relative addressing'' scheme, to obtain an absolute address, the relevant base address is taken and an offset (aka displacement) is added to it. Under this type of scheme, the base address is the lowest numbered address within a prescribed range, to facilitate adding related positive-valued offsets. In IBM System/360 architecture, the base address is a 24-bit value in a general register (extended in steps to 64 bits in z/Architecture), and the offset is a 12 bit value in the instruction (extended to 20 bits in z/Architecture). See also * Index register An index register in a computer's central processing unit, CPU is a processor register (or an assigned memory location) used for pointing to operand addresses during the run of a program. It is useful for stepping through String (computer scienc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Assembly Language
In computing, assembly language (alternatively assembler language or symbolic machine code), often referred to simply as assembly and commonly abbreviated as ASM or asm, is any low-level programming language with a very strong correspondence between the instructions in the language and the architecture's machine code instructions. Assembly language usually has one statement per machine instruction (1:1), but constants, comments, assembler directives, symbolic labels of, e.g., memory locations, registers, and macros are generally also supported. The first assembly code in which a language is used to represent machine code instructions is found in Kathleen and Andrew Donald Booth's 1947 work, ''Coding for A.R.C.''. Assembly code is converted into executable machine code by a utility program referred to as an '' assembler''. The term "assembler" is generally attributed to Wilkes, Wheeler and Gill in their 1951 book '' The Preparation of Programs for an Electronic Dig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Raising And Lowering Indices
The asterisk ( ), from Late Latin , from Ancient Greek , , "little star", is a typographical symbol. It is so called because it resembles a conventional image of a heraldic star. Computer scientists and mathematicians often vocalize it as star (as, for example, in ''the A* search algorithm'' or ''C*-algebra''). An asterisk is usually five- or six-pointed in print and six- or eight-pointed when handwritten, though more complex forms exist. Its most common use is to call out a footnote. It is also often used to censor offensive words. In computer science, the asterisk is commonly used as a wildcard character, or to denote pointers, repetition, or multiplication. History The asterisk was already in use as a symbol in ice age cave paintings. There is also a two-thousand-year-old character used by Aristarchus of Samothrace called the , , which he used when proofreading Homeric poetry to mark lines that were duplicated. Origen is known to have also used the asteriskos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Covariance And Contravariance Of Vectors
In physics, especially in multilinear algebra and tensor analysis, covariance and contravariance describe how the quantitative description of certain geometric or physical entities changes with a change of basis. Briefly, a contravariant vector is a list of numbers that transforms oppositely to a change of basis, and a covariant vector is a list of numbers that transforms in the same way. Contravariant vectors are often just called ''vectors'' and covariant vectors are called ''covectors'' or ''dual vectors''. The terms ''covariant'' and ''contravariant'' were introduced by James Joseph Sylvester in 1851. Curvilinear coordinate systems, such as cylindrical coordinates, cylindrical or spherical coordinates, are often used in physical and geometric problems. Associated with any coordinate system is a natural choice of coordinate basis for vectors based at each point of the space, and covariance and contravariance are particularly important for understanding how the coordinate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix Equation
In mathematics, a matrix (: matrices) is a rectangle, rectangular array or table of numbers, symbol (formal), symbols, or expression (mathematics), expressions, with elements or entries arranged in rows and columns, which is used to represent a mathematical object or property of such an object. For example, \begin1 & 9 & -13 \\20 & 5 & -6 \end is a matrix with two rows and three columns. This is often referred to as a "two-by-three matrix", a " matrix", or a matrix of dimension . Matrices are commonly used in linear algebra, where they represent linear maps. In geometry, matrices are widely used for specifying and representing geometric transformations (for example rotation (mathematics), rotations) and coordinate changes. In numerical analysis, many computational problems are solved by reducing them to a matrix computation, and this often involves computing with matrices of huge dimensions. Matrices are used in most areas of mathematics and scientific fields, either directly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multiplication
Multiplication is one of the four elementary mathematical operations of arithmetic, with the other ones being addition, subtraction, and division (mathematics), division. The result of a multiplication operation is called a ''Product (mathematics), product''. Multiplication is often denoted by the cross symbol, , by the mid-line dot operator, , by juxtaposition, or, in programming languages, by an asterisk, . The multiplication of whole numbers may be thought of as repeated addition; that is, the multiplication of two numbers is equivalent to adding as many copies of one of them, the ''multiplicand'', as the quantity of the other one, the ''multiplier''; both numbers can be referred to as ''factors''. This is to be distinguished from term (arithmetic), ''terms'', which are added. :a\times b = \underbrace_ . Whether the first factor is the multiplier or the multiplicand may be ambiguous or depend upon context. For example, the expression 3 \times 4 , can be phrased as "3 ti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix
Matrix (: matrices or matrixes) or MATRIX may refer to: Science and mathematics * Matrix (mathematics), a rectangular array of numbers, symbols or expressions * Matrix (logic), part of a formula in prenex normal form * Matrix (biology), the material in between a eukaryotic organism's cells * Matrix (chemical analysis), the non-analyte components of a sample * Matrix (geology), the fine-grained material in which larger objects are embedded * Matrix (composite), the constituent of a composite material * Hair matrix, produces hair * Nail matrix, part of the nail in anatomy Technology * Matrix (mass spectrometry), a compound that promotes the formation of ions * Matrix (numismatics), a tool used in coin manufacturing * Matrix (printing), a mould for casting letters * Matrix (protocol), an open standard for real-time communication * Matrix (record production), or master, a disc used in the production of phonograph records ** Matrix number, of a gramophone record * Diode matrix, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector Equation
Vector most often refers to: * Euclidean vector, a quantity with a magnitude and a direction * Disease vector, an agent that carries and transmits an infectious pathogen into another living organism Vector may also refer to: Mathematics and physics * Vector (mathematics and physics) ** Row and column vectors, single row or column matrices ** Vector quantity ** Vector space ** Vector field, a vector for each point Molecular biology * Vector (molecular biology), a DNA molecule used as a vehicle to artificially carry foreign genetic material into another cell ** Cloning vector, a small piece of DNA into which a foreign DNA fragment can be inserted for cloning purposes ** Shuttle vector, a plasmid constructed so that it can propagate in two different host species ** Viral vector, a tool commonly used by molecular biologists to deliver genetic materials into cells Computer science * Vector, a one-dimensional array data structure ** Distance-vector routing protocol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |