|
Indefinite Product
In mathematics, the indefinite product operator is the inverse operator of Q(f(x)) = \frac. It is a discrete version of the geometric integral of geometric calculus, one of the non-Newtonian calculi. Some authors use term discrete multiplicative integration. Thus :Q\left( \prod_x f(x) \right) = f(x) \, . More explicitly, if \prod_x f(x) = F(x) , then :\frac = f(x) \, . If ''F''(''x'') is a solution of this functional equation for a given ''f''(''x''), then so is ''CF''(''x'') for any constant ''C''. Therefore, each indefinite product actually represents a family of functions, differing by a multiplicative constant. Period rule If T is a period of function f(x) then :\prod _x f(Tx)=C f(Tx)^ Connection to indefinite sum Indefinite product can be expressed in terms of indefinite sum: :\prod _x f(x)= \exp \left(\sum _x \ln f(x)\right) Alternative usage Some authors use the phrase "indefinite product" in a slightly different but related way to describe a product in which th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Indefinite Sum
In discrete calculus the indefinite sum operator (also known as the antidifference operator), denoted by \sum _x or \Delta^ , is the linear operator, inverse of the forward difference operator \Delta . It relates to the forward difference operator as the indefinite integral relates to the derivative. Thus :\Delta \sum_x f(x) = f(x) \, . More explicitly, if \sum_x f(x) = F(x) , then :F(x+1) - F(x) = f(x) \, . If ''F''(''x'') is a solution of this functional equation for a given ''f''(''x''), then so is ''F''(''x'')+''C''(''x'') for any periodic function ''C''(''x'') with period 1. Therefore, each indefinite sum actually represents a family of functions. However, due to the Carlson's theorem, the solution equal to its Newton series expansion is unique up to an additive constant ''C''. This unique solution can be represented by formal power series form of the antidifference operator: \Delta^=\frac1. Fundamental theorem of discrete calculus Indefinite sums can be used to calculate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
K-function
In mathematics, the -function, typically denoted ''K''(''z''), is a generalization of the hyperfactorial to complex numbers, similar to the generalization of the factorial to the gamma function. Definition Formally, the -function is defined as :K(z)=(2\pi)^ \exp\left binom+\int_0^ \ln \Gamma(t + 1)\,dt\right It can also be given in closed form as :K(z)=\exp\bigl zeta'(-1,z)-\zeta'(-1)\bigr/math> where denotes the derivative of the Riemann zeta function, denotes the Hurwitz zeta function and :\zeta'(a,z)\ \stackrel\ \left.\frac\_. Another expression using the polygamma function is :K(z)=\exp\left psi^(z)+\frac-\frac \ln 2\pi \right/math> Or using the balanced generalization of the polygamma function: :K(z)=A \exp\left psi(-2,z)+\frac\right/math> where is the Glaisher constant. Similar to the Bohr-Mollerup Theorem for the Gamma function, the log K-function is the unique (up to an additive constant) eventually 2-convex solution to the equation \Delta f(x)=x\ln(x ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Barnes G-function
In mathematics, the Barnes G-function ''G''(''z'') is a function that is an extension of superfactorials to the complex numbers. It is related to the gamma function, the K-function and the Glaisher–Kinkelin constant, and was named after mathematician Ernest William Barnes. It can be written in terms of the double gamma function. Formally, the Barnes ''G''-function is defined in the following Weierstrass product form: : G(1+z)=(2\pi)^ \exp\left(- \frac \right) \, \prod_^\infty \left\ where \, \gamma is the Euler–Mascheroni constant, exp(''x'') = ''e''''x'' is the exponential function, and Π denotes multiplication (capital pi notation). As an entire function, ''G'' is of order two, and of infinite type. This can be deduced from the asymptotic expansion given below. Functional equation and integer arguments The Barnes ''G''-function satisfies the functional equation : G(z+1)=\Gamma(z)\, G(z) with normalisation ''G''(1) = 1. Note the similarity between the functi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Super-exponential Function
In mathematics, tetration (or hyper-4) is an operation based on iterated, or repeated, exponentiation. There is no standard notation for tetration, though \uparrow \uparrow and the left-exponent ''xb'' are common. Under the definition as repeated exponentiation, means , where ' copies of ' are iterated via exponentiation, right-to-left, i.e. the application of exponentiation n-1 times. ' is called the "height" of the function, while ' is called the "base," analogous to exponentiation. It would be read as "the th tetration of ". It is the next hyperoperation after exponentiation, but before pentation. The word was coined by Reuben Louis Goodstein from tetra- (four) and iteration. Tetration is also defined recursively as : := \begin 1 &\textn=0, \\ a^ &\textn>0, \end allowing for attempts to extend tetration to non-natural numbers such as real and complex numbers. The two inverses of tetration are called super-root and super-logarithm, analogous to the nth root and the log ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Indefinite Sum
In discrete calculus the indefinite sum operator (also known as the antidifference operator), denoted by \sum _x or \Delta^ , is the linear operator, inverse of the forward difference operator \Delta . It relates to the forward difference operator as the indefinite integral relates to the derivative. Thus :\Delta \sum_x f(x) = f(x) \, . More explicitly, if \sum_x f(x) = F(x) , then :F(x+1) - F(x) = f(x) \, . If ''F''(''x'') is a solution of this functional equation for a given ''f''(''x''), then so is ''F''(''x'')+''C''(''x'') for any periodic function ''C''(''x'') with period 1. Therefore, each indefinite sum actually represents a family of functions. However, due to the Carlson's theorem, the solution equal to its Newton series expansion is unique up to an additive constant ''C''. This unique solution can be represented by formal power series form of the antidifference operator: \Delta^=\frac1. Fundamental theorem of discrete calculus Indefinite sums can be used to calculate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Product Integral
A product integral is any Product (mathematics), product-based counterpart of the usual Summation, sum-based integral of calculus. The first product integral (''#Type I: Volterra integral, Type I'' below) was developed by the mathematician Vito Volterra in 1887 to solve systems of linear differential equations. A. Slavík''Product integration, its history and applications'' , Matfyzpress, Prague, 2007. Other examples of product integrals are the #Type II: geometric integral, geometric integral (''#Type II: geometric integral, Type II'' below), the #Type III: bigeometric integral, bigeometric integral (''#Type III: bigeometric integral, Type III'' below), and some other integrals of non-Newtonian calculus. Michael Grossman''The First Nonlinear System of Differential And Integral Calculus'' , 1979.Michael Grossman''Bigeometric Calculus: A System with a Scale-Free Derivative'' , 1983. Product integrals have found use in areas from epidemiology (the Kaplan–Meier estimator) to stochas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Derivatives And Integrals In Alternative Calculi
There are many alternatives to the classical calculus of Newton and Leibniz; for example, each of the infinitely many non-Newtonian calculi. Occasionally an alternative calculus is more suited than the classical calculus for expressing a given scientific or mathematical idea. The table below is intended to assist people working with the alternative calculus called the "geometric calculus" (or its discrete analog). Interested readers are encouraged to improve the table by inserting citations for verification, and by inserting more functions and more calculi. Table In the following table \psi(x)=\frac is the digamma function, K(x)=e^=e^ is the K-function, (!x)=\frac is subfactorial, B_a(x)=-a\zeta(-a+1,x) are the generalized to real numbers Bernoulli polynomials. See also *Indefinite product *Product integral *Fractal derivative In applied mathematics and mathematical analysis, the fractal derivative or Hausdorff derivative is a non-Newtonian generalization of the deriva ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
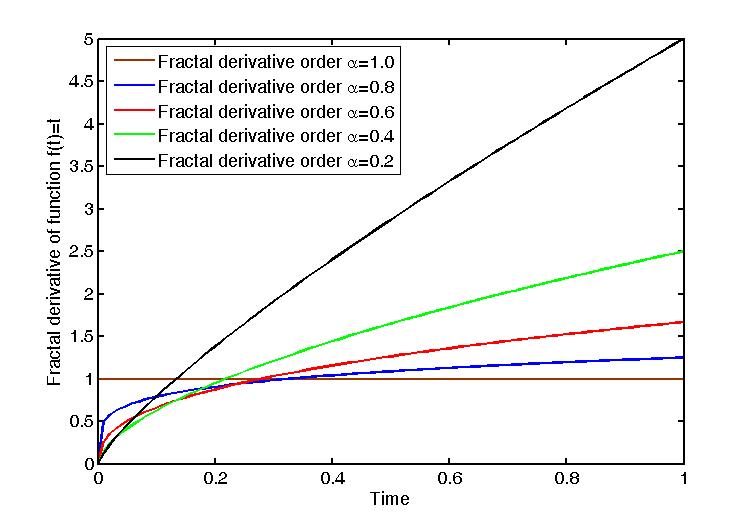
Fractal Derivative
In applied mathematics and mathematical analysis, the fractal derivative or Hausdorff derivative is a non-Newtonian generalization of the derivative dealing with the measurement of fractals, defined in fractal geometry. Fractal derivatives were created for the study of anomalous diffusion, by which traditional approaches fail to factor in the fractal nature of the media. A fractal measure ''t'' is scaled according to ''tα''. Such a derivative is local, in contrast to the similarly applied fractional derivative. Fractal calculus is formulated as a generalized of standard calculus Physical background Porous media, aquifers, turbulence, and other media usually exhibit fractal properties. Classical diffusion or dispersion laws based on random walks in free space (essentially the same result variously known as Fick's laws of diffusion, Darcy's law, and Fourier's law) are not applicable to fractal media. To address this, concepts such as distance and velocity must be redefined for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Analysis
Analysis is the branch of mathematics dealing with continuous functions, limit (mathematics), limits, and related theories, such as Derivative, differentiation, Integral, integration, measure (mathematics), measure, infinite sequences, series (mathematics), series, and analytic functions. These theories are usually studied in the context of Real number, real and Complex number, complex numbers and Function (mathematics), functions. Analysis evolved from calculus, which involves the elementary concepts and techniques of analysis. Analysis may be distinguished from geometry; however, it can be applied to any Space (mathematics), space of mathematical objects that has a definition of nearness (a topological space) or specific distances between objects (a metric space). History Ancient Mathematical analysis formally developed in the 17th century during the Scientific Revolution, but many of its ideas can be traced back to earlier mathematicians. Early results in analysis were i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |