|
Hypotrochoid
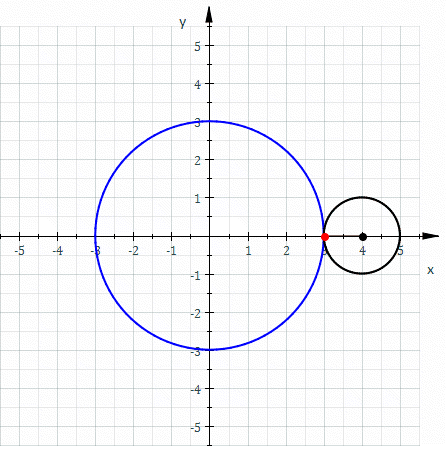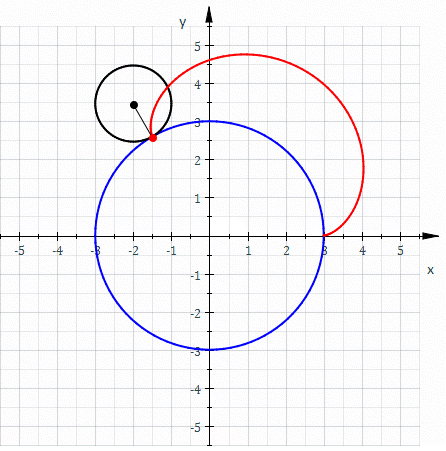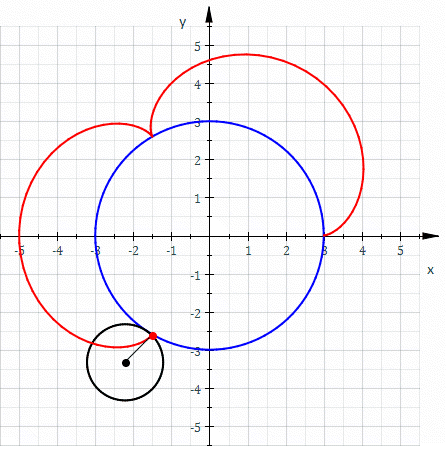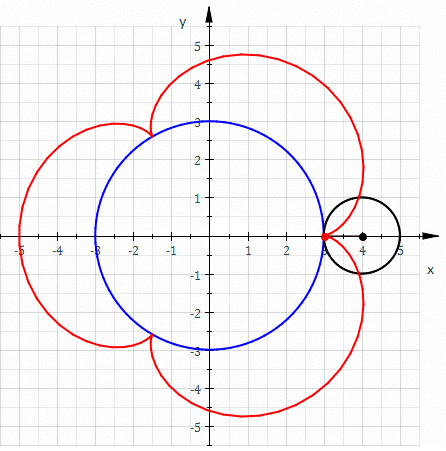
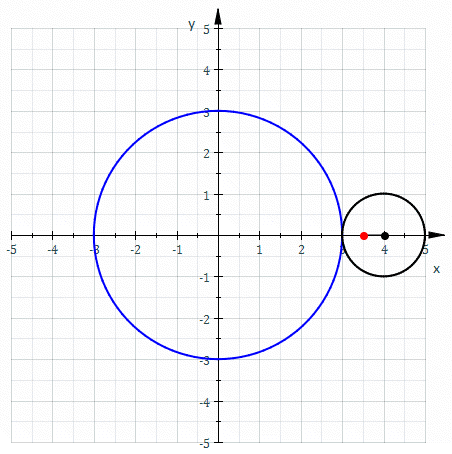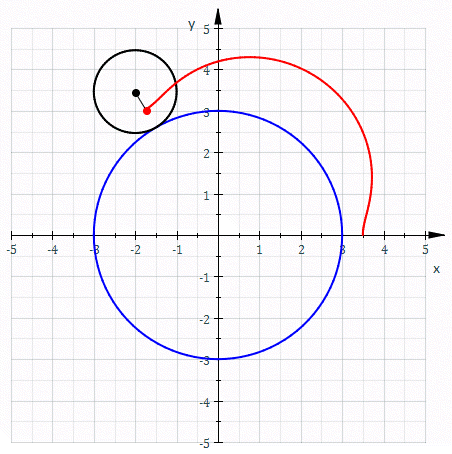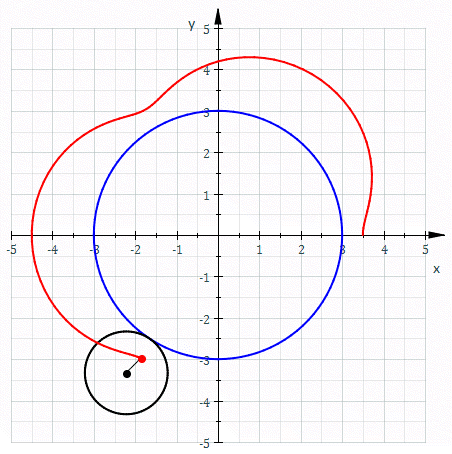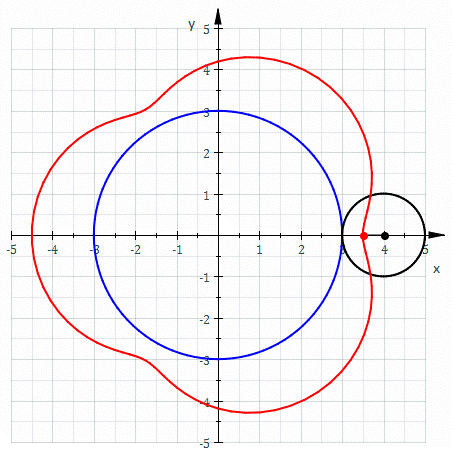
In geometry, a hypotrochoid is a roulette (curve), roulette traced by a point attached to a circle of radius rolling around the inside of a fixed circle of radius , where the point is a distance from the center of the interior circle. The parametric equations for a hypotrochoid are: :\begin & x (\theta) = (R - r)\cos\theta + d\cos\left(\theta\right) \\ & y (\theta) = (R - r)\sin\theta - d\sin\left(\theta\right) \end where is the angle formed by the horizontal and the center of the rolling circle (these are not polar equations because is not the polar angle). When measured in radian, takes values from 0 to 2 \pi \times \tfrac (where is least common multiple). Special cases include the hypocycloid with and the ellipse with and . The eccentricity of the ellipse is :e=\frac becoming 1 when d=r (see Tusi couple). The classic Spirograph toy traces out hypotrochoid and epitrochoid curves. Hypotrochoids describe the support of the eigenvalues of some random matrices with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Parametric Equation
In mathematics, a parametric equation expresses several quantities, such as the coordinates of a point (mathematics), point, as Function (mathematics), functions of one or several variable (mathematics), variables called parameters. In the case of a single parameter, parametric equations are commonly used to express the trajectory of a moving point, in which case, the parameter is often, but not necessarily, time, and the point describes a curve, called a parametric curve. In the case of two parameters, the point describes a Surface (mathematics), surface, called a parametric surface. In all cases, the equations are collectively called a parametric representation, or parametric system, or parameterization (also spelled parametrization, parametrisation) of the object. For example, the equations \begin x &= \cos t \\ y &= \sin t \end form a parametric representation of the unit circle, where is the parameter: A point is on the unit circle if and only if there is a value of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Ellipse
In mathematics, an ellipse is a plane curve surrounding two focus (geometry), focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity (mathematics), eccentricity e, a number ranging from e = 0 (the Limiting case (mathematics), limiting case of a circle) to e = 1 (the limiting case of infinite elongation, no longer an ellipse but a parabola). An ellipse has a simple algebraic solution for its area, but for Perimeter of an ellipse, its perimeter (also known as circumference), Integral, integration is required to obtain an exact solution. The largest and smallest diameters of an ellipse, also known as its width and height, are typically denoted and . An ellipse has four extreme points: two ''Vertex (geometry), vertices'' at the endpoints of the major axis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Ellipse As Hypotrochoid
In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity e, a number ranging from e = 0 (the limiting case of a circle) to e = 1 (the limiting case of infinite elongation, no longer an ellipse but a parabola). An ellipse has a simple algebraic solution for its area, but for its perimeter (also known as circumference), integration is required to obtain an exact solution. The largest and smallest diameters of an ellipse, also known as its width and height, are typically denoted and . An ellipse has four extreme points: two '' vertices'' at the endpoints of the major axis and two ''co-vertices'' at the endpoints of the minor axis. Analytically, the equation of a standard ellipse centered at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Tusi Couple
The Tusi couple (also known as Tusi's mechanism) is a mathematical device in which a small circle rotates inside a larger circle twice the diameter of the smaller circle. Rotations of the circles cause a point on the circumference of the smaller circle to Oscillation (mathematics), oscillate back and forth in linear motion along a diameter of the larger circle. The Tusi couple is a two-cusped hypocycloid. The couple was first proposed by the 13th-century Persian people, Persian Islamic astronomy, astronomer and Islamic mathematics, mathematician Nasir al-Din al-Tusi in his 1247 ''Tahrir al-Majisti'' (''Commentary on the Almagest'') as a solution for the latitudinal motion of the inferior planets and later used extensively as a substitute for the equant introduced over a thousand years earlier in Ptolemy's ''Almagest''. Original description The translation of the copy of Tusi's original description of his geometrical model alludes to at least one inversion of the model to b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hypocycloid
In geometry, a hypocycloid is a special plane curve generated by the trace of a fixed point on a small circle that rolls within a larger circle. As the radius of the larger circle is increased, the hypocycloid becomes more like the cycloid created by rolling a circle on a line. History The 2-cusped hypocycloid called Tusi couple was first described by the 13th-century Persian people, Persian Islamic astronomy, astronomer and Islamic mathematics, mathematician Nasir al-Din al-Tusi in ''Tahrir al-Majisti (Commentary on the Almagest)''. German painter and German Renaissance theorist Albrecht Dürer described epitrochoids in 1525, and later Roemer and Bernoulli concentrated on some specific hypocycloids, like the astroid, in 1674 and 1691, respectively. Properties If the rolling circle has radius , and the fixed circle has radius , then the parametric equations for the curve can be given by either: \begin & x (\theta) = (R - r) \cos \theta + r \cos \left(\frac \theta \right) \\ & ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Cycloid
In geometry, a cycloid is the curve traced by a point on a circle as it Rolling, rolls along a Line (geometry), straight line without slipping. A cycloid is a specific form of trochoid and is an example of a roulette (curve), roulette, a curve generated by a curve rolling on another curve. The cycloid, with the Cusp (singularity), cusps pointing upward, is the curve of fastest descent under uniform gravity (the brachistochrone curve). It is also the form of a curve for which the Frequency, period of an object in simple harmonic motion (rolling up and down repetitively) along the curve does not depend on the object's starting position (the tautochrone curve). In physics, when a charged particle at rest is put under a uniform Electric field, electric and magnetic field perpendicular to one another, the particle’s trajectory draws out a cycloid. History The cycloid has been called "The Helen of Geometers" as, like Helen of Troy, it caused frequent quarrels among 17th-centur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Roulette (curve)
In the differential geometry of curves, a roulette is a kind of curve, generalizing cycloids, epicycloids, hypocycloids, trochoids, epitrochoids, hypotrochoids, and involutes. On a basic level, it is the path traced by a curve while rolling on another curve without slipping. Definition Informal definition Roughly speaking, a roulette is the curve described by a point (called the ''generator'' or ''pole'') attached to a given curve as that curve rolls without slipping, along a second given curve that is fixed. More precisely, given a curve attached to a plane which is moving so that the curve rolls, without slipping, along a given curve attached to a fixed plane occupying the same space, then a point attached to the moving plane describes a curve, in the fixed plane called a roulette. Special cases and related concepts In the case where the rolling curve is a line and the generator is a point on the line, the roulette is called an involute of the fixed curve. If the rol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Rosetta (orbit)
A Rosetta orbit is a complex type of orbit. In astronomy, a Rosetta orbit occurs when there is a periastron shift during each orbital cycle. A retrograde Newtonian shift can occur when the central mass is extended rather than a point gravitational source, resulting in a non-closed orbit. A prograde relativistic shift happens because of relativistic effects from a massive gravitational source. In barred spiral galaxies with a compact, lens-shaped bar (in contrast with a box-shaped bar), the morphology of the bar is supported by stars following rosette-shaped orbits that rotate with the bar. An object approaching a black hole with an intermediate velocity (not slow enough to spiral into the hole and not fast enough to escape) enters a complex orbit pattern, bounded by a near and far distance to the hole and tracing an oscillating pattern known as a hypotrochoid. In 2020, scientists using observations made by the European Southern Observatory's Very Large Telescope revealed for the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Spirograph
Spirograph is a geometric drawing device that produces mathematical roulette curves of the variety technically known as hypotrochoids and epitrochoids. The well-known toy version was developed by British engineer Denys Fisher and first sold in 1965. The name has been a registered trademark of Hasbro Inc. since 1998 following purchase of the company that had acquired the Denys Fisher company. The Spirograph brand was relaunched worldwide in 2013, with its original product configurations, by Kahootz Toys. History In 1827, Greek-born English architect and engineer Peter Hubert Desvignes developed and advertised a "Speiragraph", a device to create elaborate spiral drawings. A man named J. Jopling soon claimed to have previously invented similar methods. When working in Vienna between 1845 and 1848, Desvignes constructed a version of the machine that would help prevent banknote forgeries, as any of the nearly endless variations of roulette patterns that it could produce were ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Epitrochoid
In geometry, an epitrochoid ( or ) is a roulette traced by a point attached to a circle of radius rolling around the outside of a fixed circle of radius , where the point is at a distance from the center of the exterior circle. The parametric equations for an epitrochoid are: :\begin & x (\theta) = (R + r)\cos\theta - d\cos\left(\theta\right) \\ & y (\theta) = (R + r)\sin\theta - d\sin\left(\theta\right) \end The parameter is geometrically the polar angle of the center of the exterior circle. (However, is not the polar angle of the point (x(\theta),y(\theta)) on the epitrochoid.) Special cases include the limaçon with and the epicycloid with . The classic Spirograph toy traces out epitrochoid and hypotrochoid curves. The paths of planets in the once popular geocentric system of deferents and epicycles are epitrochoids with d>r, for both the outer planets and the inner planets. The orbit of the Moon, when centered around the Sun, approximates an epitrochoid. The com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Roulettes (curve)
The Roulettes are the Royal Australian Air Force's formation aerobatics, aerobatic display team. They provide about 150 flying displays a year, in Australia and in friendly countries around the Southeast Asian region. The Roulettes form part of the RAAF Central Flying School (CFS) at RAAF Base East Sale, Victoria (Australia), Victoria. History and organisation The Central Flying School formed its first official aerobatic team in 1962, the ''Red Sales'', using De Havilland Vampire Mk 35 jet trainers. On 15 August 1962 the team was involved in a major incident with the loss of six lives and four aircraft. The ''Telstars'' were formed in Feb 1963 still using Vampire aircraft. They were re-equipped with Macchi MB-326 aircraft in Feb 1968, but were disbanded in Apr 1968 due to budget restraints. In 1970, the Roulettes were formed to celebrate the RAAF's 50th anniversary to be held throughout the year of 1971. The Roulettes first air show was at Point Cook in Dec 1970. Their last ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Apsidal Precession
In celestial mechanics, apsidal precession (or apsidal advance) is the precession (gradual rotation) of the line connecting the apsis, apsides (line of apsides) of an orbiting body, astronomical body's orbit. The apsides are the orbital points farthest (apoapsis) and closest (periapsis) from its primary (astronomy), primary body. The apsidal precession is the first time derivative of the argument of periapsis, one of the six main orbital elements of an orbit. Apsidal precession is considered positive when the orbit's axis rotates in the same direction as the orbital motion. An apsidal period is the time interval required for an orbit to precess through 360°, which takes the Earth about 112,000 years and the Moon about 8.85 years. History The ancient Greek astronomer Hipparchus noted the apsidal precession of the Moon's orbit (as the revolution of the Moon's apogee with a period of approximately 8.85 years); it is corrected for in the Antikythera Mechanism (circa 80 BC ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |