|
Hurwitz-stable Matrix
In mathematics, a Hurwitz-stable matrix, or more commonly simply Hurwitz matrix, is a square matrix whose eigenvalues all have strictly negative real part. Some authors also use the term stability matrix. Such matrices play an important role in control theory. Definition A square matrix A is called a Hurwitz matrix if every eigenvalue of A has strictly negative real part, that is, :\operatorname[\lambda_i] < 0\, for each eigenvalue . is also called a stable matrix, because then the ordinary differential equation, differential equation : is stability theory, asymptotically stable, that is, as If is a (matrix-valued) transfer function, then is called Hurwitz if the pole (complex analysis), poles of all elements of have negative real part. Note that it is not necessary that for a specific argument [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fixed Point (mathematics)
A fixed point (sometimes shortened to fixpoint, also known as an invariant point) is a value that does not change under a given transformation. Specifically, in mathematics, a fixed point of a function is an element that is mapped to itself by the function. In physics, the term fixed point can refer to a temperature that can be used as a reproducible reference point, usually defined by a phase change or triple point. Fixed point of a function Formally, is a fixed point of a function if belongs to both the domain and the codomain of , and . For example, if is defined on the real numbers by f(x) = x^2 - 3 x + 4, then 2 is a fixed point of , because . Not all functions have fixed points: for example, , has no fixed points, since is never equal to for any real number. In graphical terms, a fixed point means the point is on the line , or in other words the graph of has a point in common with that line. Fixed-point iteration In numerical analysis, ''fixed-poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perron–Frobenius Theorem
In matrix theory, the Perron–Frobenius theorem, proved by and , asserts that a real square matrix with positive entries has a unique largest real eigenvalue and that the corresponding eigenvector can be chosen to have strictly positive components, and also asserts a similar statement for certain classes of nonnegative matrices. This theorem has important applications to probability theory (ergodicity of Markov chains); to the theory of dynamical systems (subshifts of finite type); to economics (Okishio's theorem, Hawkins–Simon condition); to demography ( Leslie population age distribution model); to social networks ( DeGroot learning process); to Internet search engines (PageRank); and even to ranking of football teams. The first to discuss the ordering of players within tournaments using Perron–Frobenius eigenvectors is Edmund Landau. Statement Let positive and non-negative respectively describe matrices with exclusively positive real numbers as elements and matrices ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
M-matrix
In mathematics, especially linear algebra, an ''M''-matrix is a ''Z''-matrix with eigenvalues whose real parts are nonnegative. The set of non-singular ''M''-matrices are a subset of the class of ''P''-matrices, and also of the class of inverse-positive matrices (i.e. matrices with inverses belonging to the class of positive matrices). The name ''M''-matrix was seemingly originally chosen by Alexander Ostrowski in reference to Hermann Minkowski, who proved that if a Z-matrix has all of its row sums positive, then the determinant of that matrix is positive.. Characterizations An M-matrix is commonly defined as follows: Definition: Let be a real Z-matrix. That is, where for all . Then matrix ''A'' is also an ''M-matrix'' if it can be expressed in the form , where with , for all , where is at least as large as the maximum of the moduli of the eigenvalues of , and is an identity matrix. For the non-singularity of , according to the Perron–Frobenius theorem, it must ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
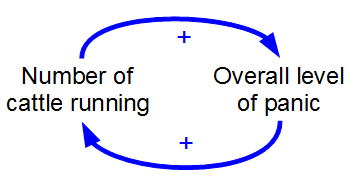
Positive Feedback
Positive feedback (exacerbating feedback, self-reinforcing feedback) is a process that occurs in a feedback loop which exacerbates the effects of a small disturbance. That is, the effects of a perturbation on a system include an increase in the magnitude of the perturbation. That is, ''A produces more of B which in turn produces more of A''.Keesing, R.M. (1981). Cultural anthropology: A contemporary perspective (2nd ed.) p.149. Sydney: Holt, Rinehard & Winston, Inc. In contrast, a system in which the results of a change act to reduce or counteract it has negative feedback. Both concepts play an important role in science and engineering, including biology, chemistry, and cybernetics. Mathematically, positive feedback is defined as a positive loop gain around a closed loop of cause and effect. That is, positive feedback is in phase with the input, in the sense that it adds to make the input larger. Positive feedback tends to cause system instability. When the loop gain is p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Negative Feedback
Negative feedback (or balancing feedback) occurs when some function of the output of a system, process, or mechanism is fed back in a manner that tends to reduce the fluctuations in the output, whether caused by changes in the input or by other disturbances. Whereas positive feedback tends to lead to instability via exponential growth, oscillation or chaotic behavior, negative feedback generally promotes stability. Negative feedback tends to promote a settling to equilibrium, and reduces the effects of perturbations. Negative feedback loops in which just the right amount of correction is applied with optimum timing can be very stable, accurate, and responsive. Negative feedback is widely used in mechanical and electronic engineering, and also within living organisms, and can be seen in many other fields from chemistry and economics to physical systems such as the climate. General negative feedback systems are studied in control systems engineering. Negative feedback l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jacobian Matrix And Determinant
In vector calculus, the Jacobian matrix (, ) of a vector-valued function of several variables is the matrix of all its first-order partial derivatives. When this matrix is square, that is, when the function takes the same number of variables as input as the number of vector components of its output, its determinant is referred to as the Jacobian determinant. Both the matrix and (if applicable) the determinant are often referred to simply as the Jacobian in literature. Suppose is a function such that each of its first-order partial derivatives exist on . This function takes a point as input and produces the vector as output. Then the Jacobian matrix of is defined to be an matrix, denoted by , whose th entry is \mathbf J_ = \frac, or explicitly :\mathbf J = \begin \dfrac & \cdots & \dfrac \end = \begin \nabla^ f_1 \\ \vdots \\ \nabla^ f_m \end = \begin \dfrac & \cdots & \dfrac\\ \vdots & \ddots & \vdots\\ \dfrac & \cd ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
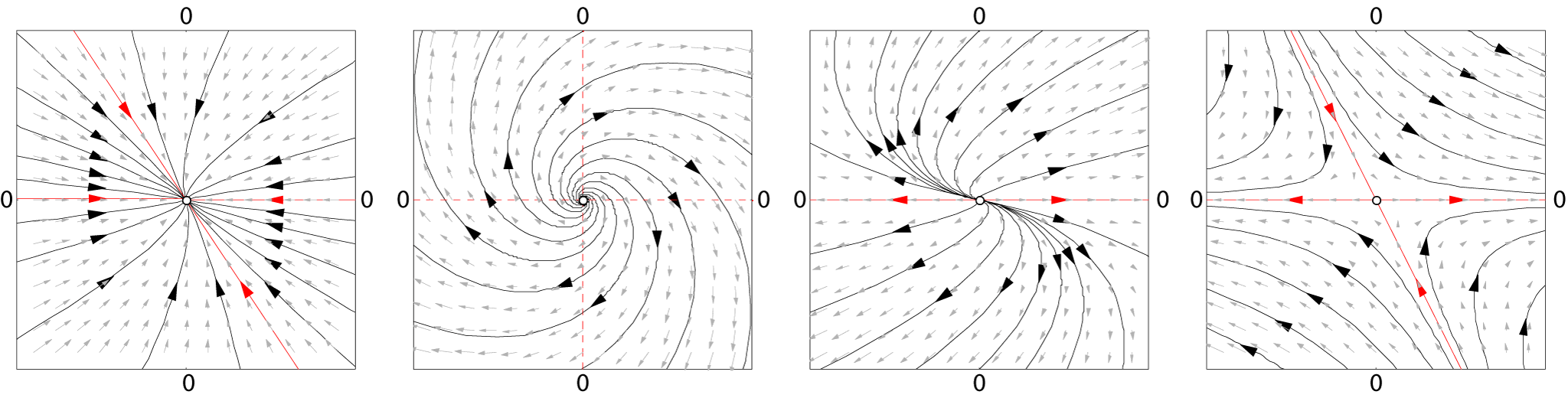
Asymptotic Stability
Various types of Stability theory, stability may be discussed for the solutions of differential equations or difference equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. This may be discussed by the theory of Aleksandr Lyapunov. In simple terms, if the solutions that start out near an equilibrium point x_e stay near x_e forever, then x_e is Lyapunov stable. More strongly, if x_e is Lyapunov stable and all solutions that start out near x_e converge to x_e, then x_e is Asymptotic analysis, asymptotically stable. The notion of exponential stability guarantees a minimal rate of decay, i.e., an estimate of how quickly the solutions converge. The idea of Lyapunov stability can be extended to infinite-dimensional manifolds, where it is known as structural stability, which concerns the behavior of different but "nearby" solutions to differential equations. Input-to-state stability (ISS) applies Ly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamical System (definition)
In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, the random motion of particles in the air, and the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a set, without the need of a smooth space-time structure defined on it. At any given time, a dynamical system has a state representing a point in an appropriate state space. This state is often given by a tuple of real numbers or by a vector in a geometrical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equilibrium Point
In mathematics, specifically in differential equations, an equilibrium point is a constant solution to a differential equation. Formal definition The point \tilde\in \mathbb^n is an equilibrium point for the differential equation :\frac = \mathbf(t,\mathbf) if \mathbf(t,\tilde)=\mathbf for all t. Similarly, the point \tilde\in \mathbb^n is an equilibrium point (or fixed point) for the difference equation :\mathbf_ = \mathbf(k,\mathbf_k) if \mathbf(k,\tilde)= \tilde for k=0,1,2,\ldots. Equilibria can be classified by looking at the signs of the eigenvalues of the linearization of the equations about the equilibria. That is to say, by evaluating the Jacobian matrix at each of the equilibrium points of the system, and then finding the resulting eigenvalues, the equilibria can be categorized. Then the behavior of the system in the neighborhood of each equilibrium point can be qualitatively determined, (or even quantitatively determined, in some instances), by finding t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamical System
In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, the random motion of particles in the air, and the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a set, without the need of a smooth space-time structure defined on it. At any given time, a dynamical system has a state representing a point in an appropriate state space. This state is often given by a tuple of real numbers or by a vector in a geome ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prentice Hall
Prentice Hall was an American major educational publisher owned by Savvas Learning Company. Prentice Hall publishes print and digital content for the 6–12 and higher-education market, and distributes its technical titles through the Safari Books Online e-reference service. History On October 13, 1913, law professor Charles Gerstenberg and his student Richard Ettinger founded Prentice Hall. Gerstenberg and Ettinger took their mothers' maiden names, Prentice and Hall, to name their new company. Prentice Hall became known as a publisher of trade books by authors such as Norman Vincent Peale; elementary, secondary, and college textbooks; loose-leaf information services; and professional books. Prentice Hall acquired the training provider Deltak in 1979. Prentice Hall was acquired by Gulf+Western in 1984, and became part of that company's publishing division Simon & Schuster. S&S sold several Prentice Hall subsidiaries: Deltak and Resource Systems were sold to National Education ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |