|
High-leverage Point
In statistics and in particular in regression analysis, leverage is a measure of how far away the independent variable values of an observation are from those of the other observations. ''High-leverage points'', if any, are outliers with respect to the independent variables. That is, high-leverage points have no neighboring points in \mathbb^ space, where '''' is the number of independent variables in a regression model. This makes the fitted model likely to pass close to a high leverage observation. Hence high-leverage points have the potential to cause large changes in the parameter estimates when they are deleted i.e., to be influential points. Although an influential point will typically have high leverage, a high leverage point is not necessarily an influential point. The leverage is typically defined as the diagonal elements of the hat matrix. Definition and interpretations Consider the linear regression model _i = \boldsymbol_i^\boldsymbol+_i, i=1,\, 2,\ldots,\, n. That is, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ''wikt:Statistik#German, Statistik'', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
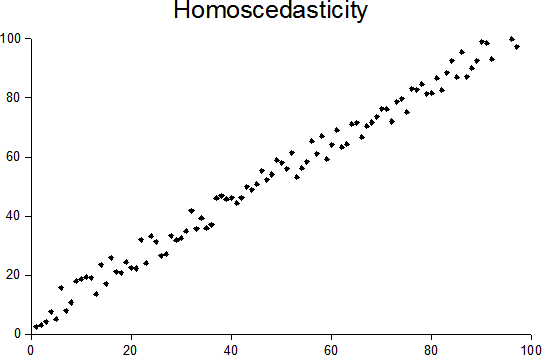Homoscedastic
In statistics, a sequence (or a vector) of random variables is homoscedastic () if all its random variables have the same finite variance. This is also known as homogeneity of variance. The complementary notion is called heteroscedasticity. The spellings ''homoskedasticity'' and ''heteroskedasticity'' are also frequently used. Assuming a variable is homoscedastic when in reality it is heteroscedastic () results in unbiased but inefficient point estimates and in biased estimates of standard errors, and may result in overestimating the goodness of fit as measured by the Pearson coefficient. The existence of heteroscedasticity is a major concern in regression analysis and the analysis of variance, as it invalidates statistical tests of significance that assume that the modelling errors all have the same variance. While the ordinary least squares estimator is still unbiased in the presence of heteroscedasticity, it is inefficient and generalized least squares should be used i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
DFFITS
DFFIT and DFFITS ("difference in fit(s)") are diagnostics meant to show how influential a point is in a statistical regression, first proposed in 1980. DFFIT is the change in the predicted value for a point, obtained when that point is left out of the regression: :\text = \widehat - \widehat where \widehat and \widehat are the prediction for point ''i'' with and without point ''i'' included in the regression. DFFITS is the Studentized DFFIT, where Studentization is achieved by dividing by the estimated standard deviation of the fit at that point: :\text = where s_ is the standard error estimated without the point in question, and h_ is the leverage for the point. DFFITS also equals the products of the externally Studentized residual (t_) and the leverage factor (\sqrt): :\text = t_ \sqrt Thus, for low leverage points, DFFITS is expected to be small, whereas as the leverage goes to 1 the distribution of the DFFITS value widens infinitely. For a perfectly balanced experi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cook's Distance
In statistics, Cook's distance or Cook's ''D'' is a commonly used estimate of the influence of a data point when performing a least-squares regression analysis. In a practical ordinary least squares analysis, Cook's distance can be used in several ways: to indicate influential data points that are particularly worth checking for validity; or to indicate regions of the design space where it would be good to be able to obtain more data points. It is named after the American statistician R. Dennis Cook, who introduced the concept in 1977. Definition Data points with large residuals (outliers) and/or high leverage may distort the outcome and accuracy of a regression. Cook's distance measures the effect of deleting a given observation. Points with a large Cook's distance are considered to merit closer examination in the analysis. For the algebraic expression, first define : \underset = \underset \quad \underset \quad + \quad \underset where \boldsymbol \sim \mathcal\left( 0, \sigma^ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Leverage
In regression analysis, partial leverage (PL) is a measure of the contribution of the individual independent variables to the total leverage of each observation. That is, if ''h''''i'' is the ''i''th element of the diagonal of the hat matrix, PL is a measure of how ''h''''i'' changes as a variable is added to the regression model. It is computed as: : \left(\mathrm_j\right)_i = \frac where :''j'' = index of independent variable :''i'' = index of observation :''X''''j''· 'j''/sub> = residuals from regressing ''X''''j'' against the remaining independent variables Note that the partial leverage is the leverage of the ''i''th point in the partial regression plot for the ''j''th variable. Data points with large partial leverage for an independent variable can exert undue influence on the selection of that variable in automatic regression model building procedures. See also * Leverage * Partial residual plot * Partial regression plot * Variance inflation factor for a multi-lin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mahalanobis Distance
The Mahalanobis distance is a measure of the distance between a point ''P'' and a distribution ''D'', introduced by P. C. Mahalanobis in 1936. Mahalanobis's definition was prompted by the problem of identifying the similarities of skulls based on measurements in 1927. It is a multi-dimensional generalization of the idea of measuring how many standard deviations away ''P'' is from the mean of ''D''. This distance is zero for ''P'' at the mean of ''D'' and grows as ''P'' moves away from the mean along each principal component axis. If each of these axes is re-scaled to have unit variance, then the Mahalanobis distance corresponds to standard Euclidean distance in the transformed space. The Mahalanobis distance is thus unitless, scale-invariant, and takes into account the correlations of the data set. Definition Given a probability distribution Q on \R^N, with mean \vec = (\mu_1, \mu_2, \mu_3, \dots , \mu_N)^\mathsf and positive-definite covariance matrix S, the Mahalanobis dis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projection Matrix
In statistics, the projection matrix (\mathbf), sometimes also called the influence matrix or hat matrix (\mathbf), maps the vector of response values (dependent variable values) to the vector of fitted values (or predicted values). It describes the influence each response value has on each fitted value. The diagonal elements of the projection matrix are the leverages, which describe the influence each response value has on the fitted value for that same observation. Definition If the vector of response values is denoted by \mathbf and the vector of fitted values by \mathbf, :\mathbf = \mathbf \mathbf. As \mathbf is usually pronounced "y-hat", the projection matrix \mathbf is also named ''hat matrix'' as it "puts a hat on \mathbf". The element in the ''i''th row and ''j''th column of \mathbf is equal to the covariance between the ''j''th response value and the ''i''th fitted value, divided by the variance of the former: :p_ = \frac Application for residuals The formula for the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Python (programming Language)
Python is a high-level, general-purpose programming language. Its design philosophy emphasizes code readability with the use of significant indentation. Python is dynamically-typed and garbage-collected. It supports multiple programming paradigms, including structured (particularly procedural), object-oriented and functional programming. It is often described as a "batteries included" language due to its comprehensive standard library. Guido van Rossum began working on Python in the late 1980s as a successor to the ABC programming language and first released it in 1991 as Python 0.9.0. Python 2.0 was released in 2000 and introduced new features such as list comprehensions, cycle-detecting garbage collection, reference counting, and Unicode support. Python 3.0, released in 2008, was a major revision that is not completely backward-compatible with earlier versions. Python 2 was discontinued with version 2.7.18 in 2020. Python consistently ranks as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
R (programming Language)
R is a programming language for statistical computing and graphics supported by the R Core Team and the R Foundation for Statistical Computing. Created by statisticians Ross Ihaka and Robert Gentleman, R is used among data miners, bioinformaticians and statisticians for data analysis and developing statistical software. Users have created packages to augment the functions of the R language. According to user surveys and studies of scholarly literature databases, R is one of the most commonly used programming languages used in data mining. R ranks 12th in the TIOBE index, a measure of programming language popularity, in which the language peaked in 8th place in August 2020. The official R software environment is an open-source free software environment within the GNU package, available under the GNU General Public License. It is written primarily in C, Fortran, and R itself (partially self-hosting). Precompiled executables are provided for various operating systems. R ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Regression Plot
In applied statistics, a partial regression plot attempts to show the effect of adding another variable to a model that already has one or more independent variables. Partial regression plots are also referred to as added variable plots, adjusted variable plots, and individual coefficient plots. When performing a linear regression with a single independent variable, a scatter plot of the response variable against the independent variable provides a good indication of the nature of the relationship. If there is more than one independent variable, things become more complicated. Although it can still be useful to generate scatter plots of the response variable against each of the independent variables, this does not take into account the effect of the other independent variables in the model. Calculation Partial regression plots are formed by: #Computing the residuals of regressing the response variable against the independent variables but omitting ''X''i #Computing the residuals fr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Errors And Residuals In Statistics
In statistics and optimization, errors and residuals are two closely related and easily confused measures of the deviation of an observed value of an element of a statistical sample from its "true value" (not necessarily observable). The error of an observation is the deviation of the observed value from the true value of a quantity of interest (for example, a population mean). The residual is the difference between the observed value and the ''estimated'' value of the quantity of interest (for example, a sample mean). The distinction is most important in regression analysis, where the concepts are sometimes called the regression errors and regression residuals and where they lead to the concept of studentized residuals. In econometrics, "errors" are also called disturbances. Introduction Suppose there is a series of observations from a univariate distribution and we want to estimate the mean of that distribution (the so-called location model). In this case, the errors are th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Independent Variable
Dependent and independent variables are variables in mathematical modeling, statistical modeling and experimental sciences. Dependent variables receive this name because, in an experiment, their values are studied under the supposition or demand that they depend, by some law or rule (e.g., by a mathematical function), on the values of other variables. Independent variables, in turn, are not seen as depending on any other variable in the scope of the experiment in question. In this sense, some common independent variables are time, space, density, mass, fluid flow rate, and previous values of some observed value of interest (e.g. human population size) to predict future values (the dependent variable). Of the two, it is always the dependent variable whose variation is being studied, by altering inputs, also known as regressors in a statistical context. In an experiment, any variable that can be attributed a value without attributing a value to any other variable is called an ind ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
