|
Hermitian Wavelet
Hermitian wavelets are a family of continuous wavelets, used in the continuous wavelet transform. The n^\textrm Hermitian wavelet is defined as the n^\textrm derivative of a Gaussian distribution: \Psi_(t)=(2n)^c_He_\left(t\right)e^ where He_\left(\right) denotes the n^\textrm Hermite polynomial. The normalisation coefficient c_ is given by: c_ = \left(n^\Gamma(n+\frac)\right)^ = \left(n^\sqrt2^(2n-1)!!\right)^\quad n\in\mathbb. The prefactor C_ in the resolution of the identity of the continuous wavelet transform for this wavelet is given by: C_=\frac i.e. Hermitian wavelets are admissible for all positive n. In computer vision and image processing, Gaussian derivative operators of different orders are frequently used as a basis for expressing various types of visual operations; see scale space and N-jet. Examples of Hermitian wavelets: Starting from Gaussian function with \mu=0, \sigma=1: f(t) = \pi^e^ the first 3 derivatives read as, :\begin f'(t) & ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous Wavelet
{{Unreferenced, date=December 2009 In numerical analysis, continuous wavelets are functions used by the continuous wavelet transform. These functions are defined as analytical expressions, as functions either of time or of frequency. Most of the continuous wavelets are used for both wavelet decomposition and composition transforms. That is they are the continuous counterpart of orthogonal wavelets. The following continuous wavelets have been invented for various applications: * Poisson wavelet * Morlet wavelet * Modified Morlet wavelet * Mexican hat wavelet * Complex Mexican hat wavelet * Shannon wavelet * Meyer wavelet * Difference of Gaussians * Hermitian wavelet * Beta wavelet * Causal wavelet * μ wavelets * Cauchy wavelet * Addison wavelet See also *Wavelet A wavelet is a wave-like oscillation with an amplitude that begins at zero, increases or decreases, and then returns to zero one or more times. Wavelets are termed a "brief oscillation". A taxonomy of wavelets has ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous Wavelet Transform
Continuity or continuous may refer to: Mathematics * Continuity (mathematics), the opposing concept to discreteness; common examples include ** Continuous probability distribution or random variable in probability and statistics ** Continuous game, a generalization of games used in game theory ** Law of Continuity, a heuristic principle of Gottfried Leibniz * Continuous function, in particular: ** Continuity (topology), a generalization to functions between topological spaces ** Scott continuity, for functions between posets ** Continuity (set theory), for functions between ordinals ** Continuity (category theory), for functors ** Graph continuity, for payoff functions in game theory * Continuity theorem may refer to one of two results: ** Lévy's continuity theorem, on random variables ** Kolmogorov continuity theorem, on stochastic processes * In geometry: ** Parametric continuity, for parametrised curves ** Geometric continuity, a concept primarily applied to the conic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
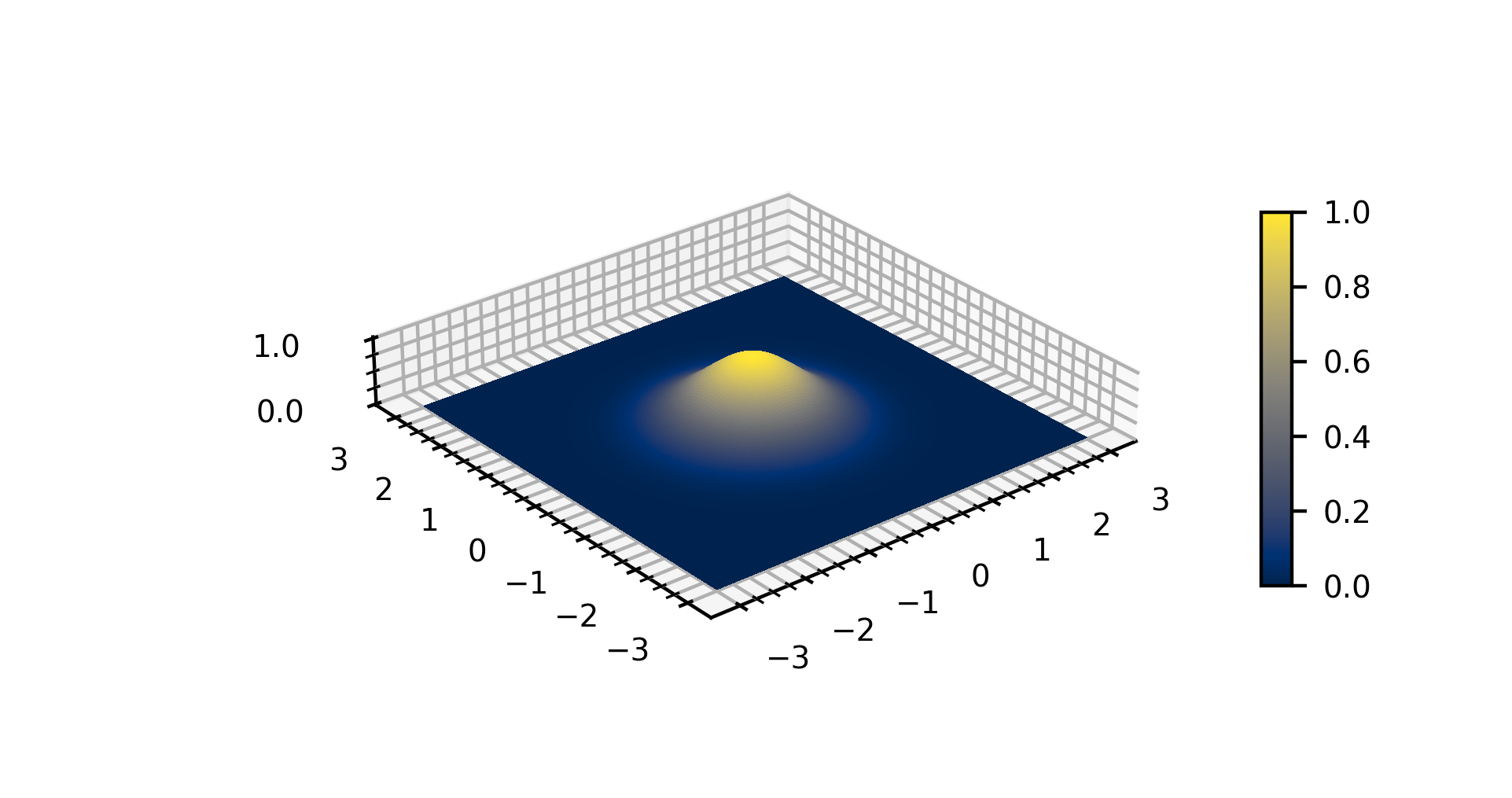
Gaussian Distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is : f(x) = \frac e^ The parameter \mu is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma is its standard deviation. The variance of the distribution is \sigma^2. A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution converges to a normal distr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hermite Polynomial
In mathematics, the Hermite polynomials are a classical orthogonal polynomial sequence. The polynomials arise in: * signal processing as Hermitian wavelets for wavelet transform analysis * probability, such as the Edgeworth series, as well as in connection with Brownian motion; * combinatorics, as an example of an Appell sequence, obeying the umbral calculus; * numerical analysis as Gaussian quadrature; * physics, where they give rise to the eigenstates of the quantum harmonic oscillator; and they also occur in some cases of the heat equation (when the term \beginxu_\end is present); * systems theory in connection with nonlinear operations on Gaussian noise. * random matrix theory in Gaussian ensembles. Hermite polynomials were defined by Pierre-Simon Laplace in 1810, though in scarcely recognizable form, and studied in detail by Pafnuty Chebyshev in 1859. Chebyshev's work was overlooked, and they were named later after Charles Hermite, who wrote on the polynomials in 18 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computer Vision
Computer vision is an Interdisciplinarity, interdisciplinary scientific field that deals with how computers can gain high-level understanding from digital images or videos. From the perspective of engineering, it seeks to understand and automate tasks that the human visual system can do. Computer vision tasks include methods for image sensor, acquiring, Image processing, processing, Image analysis, analyzing and understanding digital images, and extraction of high-dimensional data from the real world in order to produce numerical or symbolic information, e.g. in the forms of decisions. Understanding in this context means the transformation of visual images (the input of the retina) into descriptions of the world that make sense to thought processes and can elicit appropriate action. This image understanding can be seen as the disentangling of symbolic information from image data using models constructed with the aid of geometry, physics, statistics, and learning theory. The scien ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Image Processing
An image is a visual representation of something. It can be two-dimensional, three-dimensional, or somehow otherwise feed into the visual system to convey information. An image can be an artifact, such as a photograph or other two-dimensional picture, that resembles a subject. In the context of signal processing, an image is a distributed amplitude of color(s). In optics, the term “image” may refer specifically to a 2D image. An image does not have to use the entire visual system to be a visual representation. A popular example of this is of a greyscale image, which uses the visual system's sensitivity to brightness across all wavelengths, without taking into account different colors. A black and white visual representation of something is still an image, even though it does not make full use of the visual system's capabilities. Images are typically still, but in some cases can be moving or animated. Characteristics Images may be two or three- dimensional, such as a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scale Space
Scale-space theory is a framework for multi-scale signal representation developed by the computer vision, image processing and signal processing communities with complementary motivations from physics and biological vision. It is a formal theory for handling image structures at different scales, by representing an image as a one-parameter family of smoothed images, the scale-space representation, parametrized by the size of the smoothing kernel used for suppressing fine-scale structures.Ijima, T. "Basic theory on normalization of pattern (in case of typical one-dimensional pattern)". Bull. Electrotech. Lab. 26, 368– 388, 1962. (in Japanese) The parameter t in this family is referred to as the ''scale parameter'', with the interpretation that image structures of spatial size smaller than about \sqrt have largely been smoothed away in the scale-space level at scale t. The main type of scale space is the ''linear (Gaussian) scale space'', which has wide applicability as well as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
N-jet
An ''N''-jet is the set of (partial) derivatives of a function f(x) up to order ''N''. Specifically, in the area of computer vision, the ''N''-jet is usually computed from a scale space representation L of the input image f(x, y), and the partial derivatives of L are used as a basis for expressing various types of visual modules. For example, algorithms for tasks such as feature detection, feature classification, stereo matching, tracking and object recognition can be expressed in terms of ''N''-jets computed at one or several scales in scale space. See also * Scale space implementation * Jet (mathematics) In mathematics, the jet is an operation that takes a differentiable function ''f'' and produces a polynomial, the truncated Taylor polynomial of ''f'', at each point of its domain. Although this is the definition of a jet, the theory of jets regar ... References Computer vision Image processing {{mathanalysis-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gaussian Function
In mathematics, a Gaussian function, often simply referred to as a Gaussian, is a function of the base form f(x) = \exp (-x^2) and with parametric extension f(x) = a \exp\left( -\frac \right) for arbitrary real constants , and non-zero . It is named after the mathematician Carl Friedrich Gauss. The graph of a Gaussian is a characteristic symmetric " bell curve" shape. The parameter is the height of the curve's peak, is the position of the center of the peak, and (the standard deviation, sometimes called the Gaussian RMS width) controls the width of the "bell". Gaussian functions are often used to represent the probability density function of a normally distributed random variable with expected value and variance . In this case, the Gaussian is of the form g(x) = \frac \exp\left( -\frac \frac \right). Gaussian functions are widely used in statistics to describe the normal distributions, in signal processing to define Gaussian filters, in image processing where two-di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wavelet
A wavelet is a wave-like oscillation with an amplitude that begins at zero, increases or decreases, and then returns to zero one or more times. Wavelets are termed a "brief oscillation". A taxonomy of wavelets has been established, based on the number and direction of its pulses. Wavelets are imbued with specific properties that make them useful for signal processing. For example, a wavelet could be created to have a frequency of Middle C and a short duration of roughly one tenth of a second. If this wavelet were to be convolved with a signal created from the recording of a melody, then the resulting signal would be useful for determining when the Middle C note appeared in the song. Mathematically, a wavelet correlates with a signal if a portion of the signal is similar. Correlation is at the core of many practical wavelet applications. As a mathematical tool, wavelets can be used to extract information from many different kinds of data, including but not limited to au ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
_(cropped).png)