|
Heptagonal Number
In mathematics, a heptagonal number is a figurate number that is constructed by combining heptagons with ascending size. The ''n''-th heptagonal number is given by the formula :H_n=\frac. The first few heptagonal numbers are: : 0, 1, 7, 18, 34, 55, 81, 112, 148, 189, 235, 286, 342, 403, 469, 540, 616, 697, 783, 874, 970, 1071, 1177, 1288, 1404, 1525, 1651, 1782, … Parity The parity of heptagonal numbers follows the pattern odd-odd-even-even. Like square numbers, the digital root in base 10 of a heptagonal number can only be 1, 4, 7 or 9. Five times a heptagonal number, plus 1 equals a triangular number. Additional properties * The heptagonal numbers have several notable formulas: :H_=H_m+H_n+5mn :H_=H_m+H_n-5mn+3n :H_m-H_n=\frac :40H_n+9=(10n-3)^2 Sum of reciprocals A formula for the sum of the reciprocals of the heptagonal numbers is given by: : \begin\sum_^\infty \frac &= \frac+\frac\ln(5)+\frac\ln\left(\frac\sqrt\right)+\frac\ln\left(\frac\sqrt\right)\\ &=\fra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Digital Root
The digital root (also repeated digital sum) of a natural number in a given radix is the (single digit) value obtained by an iterative process of summing digits, on each iteration using the result from the previous iteration to compute a digit sum. The process continues until a single-digit number is reached. For example, in base 10, the digital root of the number 12345 is 6 because the sum of the digits in the number is 1 + 2 + 3 + 4 + 5 = 15, then the addition process is repeated again for the resulting number 15, so that the sum of 1 + 5 equals 6, which is the digital root of that number. In base 10, this is equivalent to taking the remainder upon division by 9 (except when the digital root is 9, where the remainder upon division by 9 will be 0), which allows it to be used as a divisibility rule. Formal definition Let n be a natural number. For base b > 1, we define the digit sum F_ : \mathbb \rightarrow \mathbb to be the following: :F_(n) = \sum_^ d_i where k = \lfloor \log_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Root
In mathematics, a square root of a number is a number such that y^2 = x; in other words, a number whose ''square'' (the result of multiplying the number by itself, or y \cdot y) is . For example, 4 and −4 are square roots of 16 because 4^2 = (-4)^2 = 16. Every nonnegative real number has a unique nonnegative square root, called the ''principal square root'' or simply ''the square root'' (with a definite article, see below), which is denoted by \sqrt, where the symbol "\sqrt" is called the '' radical sign'' or ''radix''. For example, to express the fact that the principal square root of 9 is 3, we write \sqrt = 3. The term (or number) whose square root is being considered is known as the ''radicand''. The radicand is the number or expression underneath the radical sign, in this case, 9. For non-negative , the principal square root can also be written in exponent notation, as x^. Every positive number has two square roots: \sqrt (which is positive) and -\sqrt (which i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Golden Ratio
In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their summation, sum to the larger of the two quantities. Expressed algebraically, for quantities and with , is in a golden ratio to if \frac = \frac = \varphi, where the Greek letter Phi (letter), phi ( or ) denotes the golden ratio. The constant satisfies the quadratic equation and is an irrational number with a value of The golden ratio was called the extreme and mean ratio by Euclid, and the divine proportion by Luca Pacioli; it also goes by other names. Mathematicians have studied the golden ratio's properties since antiquity. It is the ratio of a regular pentagon's diagonal to its side and thus appears in the Straightedge and compass construction, construction of the dodecahedron and icosahedron. A golden rectangle—that is, a rectangle with an aspect ratio of —may be cut into a square and a smaller rectangle with the same aspect ratio. The golden ratio has bee ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sums Of Reciprocals
In mathematics and especially number theory, the sum of reciprocals (or sum of inverses) generally is computed for the reciprocals of some or all of the positive integers (counting numbers)—that is, it is generally the sum of unit fractions. If infinitely many numbers have their reciprocals summed, generally the terms are given in a certain sequence and the first ''n'' of them are summed, then one more is included to give the sum of the first ''n''+1 of them, etc. If only finitely many numbers are included, the key issue is usually to find a simple expression for the value of the sum, or to require the sum to be less than a certain value, or to determine whether the sum is ever an integer. For an infinite series of reciprocals, the issues are twofold: First, does the sequence of sums diverge—that is, does it eventually exceed any given number—or does it converge, meaning there is some number that it gets arbitrarily close to without ever exceeding it? (A set of posit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fibonacci Quarterly
The ''Fibonacci Quarterly'' is a scientific journal on mathematical topics related to the Fibonacci numbers, published four times per year. It is the primary publication of The Fibonacci Association, which has published it since 1963. Its founding editors were Verner Emil Hoggatt Jr. and Alfred Brousseau; by Clark Kimberling the present editor is Professor Curtis Cooper of the Mathematics Department of the University of Central Missouri. The ''Fibonacci Quarterly'' has an editorial board of nineteen members and is overseen by the nine-me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diophantine Equation
''Diophantine'' means pertaining to the ancient Greek mathematician Diophantus. A number of concepts bear this name: *Diophantine approximation In number theory, the study of Diophantine approximation deals with the approximation of real numbers by rational numbers. It is named after Diophantus of Alexandria. The first problem was to know how well a real number can be approximated ... * Diophantine equation * Diophantine quintuple * Diophantine set {{disambig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pell Number
In mathematics, the Pell numbers are an infinite sequence of integers, known since ancient times, that comprise the denominators of the closest rational approximations to the square root of 2. This sequence of approximations begins , , , , and , so the sequence of Pell numbers begins with 1, 2, 5, 12, and 29. The numerators of the same sequence of approximations are half the companion Pell numbers or Pell–Lucas numbers; these numbers form a second infinite sequence that begins with 2, 6, 14, 34, and 82. Both the Pell numbers and the companion Pell numbers may be calculated by means of a recurrence relation similar to that for the Fibonacci numbers, and both sequences of numbers grow exponentially, proportionally to powers of the silver ratio 1 + . As well as being used to approximate the square root of two, Pell numbers can be used to find square triangular numbers, to construct integer approximations to the right isosceles triangle, and to solve certain combina ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
99 (number)
99 (ninety-nine) is the natural number In mathematics, the natural numbers are the numbers 0, 1, 2, 3, and so on, possibly excluding 0. Some start counting with 0, defining the natural numbers as the non-negative integers , while others start with 1, defining them as the positive in ... following 98 and preceding 100. In mathematics 99 is: *a composite number; a square-prime, of the form (''p''2, q). It is the 11th composite number of this form and the third of the form (32, q). It has an aliquot sum of 57, within an aliquot sequence of two composite numbers (99, 57, 23, 1,0), to the Prime in the 23-aliquot tree. *a Kaprekar number *a lucky number *a palindromic number in base ten *the ninth repdigit *the sum of the cubes of three consecutive integers: 99 = 23 + 33 + 43. *the sum of the sums of the divisors of the first 11 positive integers. * ".99" is frequently used as a price ender in pricing. See also * 99 (other) References External links ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
70 (number)
70 (seventy) is the natural number following 69 and preceding 71. Mathematics Properties of the integer 70 is the fourth discrete sphenic number, as the first of the form 2 \times 5 \times r. It is the smallest weird number, a natural number that is abundant but not semiperfect, where it is also the second-smallest primitive abundant number, after 20. 70 is in equivalence with the sum between the smallest number that is the sum of ''two'' abundant numbers, and the largest that is not ( 24, 46). 70 is the tenth Erdős–Woods number, since it is possible to find sequences of seventy consecutive integers such that each inner member shares a factor with either the first or the last member. It is also the sixth Pell number, preceding the tenth prime number 29, in the sequence \. 70 is a palindromic number in bases 9 (779), 13 (5513) and 34 (2234). Happy number 70 is the thirteenth happy number in decimal, where 7 is the first such number greater than 1 in base ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
46 (number)
46 (forty-six) is the natural number following 45 (number), 45 and preceding 47 (number), 47. In mathematics Forty-six is * thirteenth discrete semiprime (2 \times 23) and the eighth of the form (2.q), where q is a higher prime, * with an aliquot sum of 26 (number), 26; a semiprime, in an aliquot sequence of six composite numbers (46, 26,16 (number), 16, 15 (number), 15, 9 (number), 9, 4 (number), 4, 3 (number), 3, 1 (number), 1, 0) in the prime 3 (number), 3-aliquot tree, * a Wedderburn-Etherington number, * the second non-trivial nonagonal number, enneagonal number, after 24 (number), 24, * a centered triangular number, * the number of parallelogram polyominoes with 6 cells. * the amount of prime numbers in between 1 and 200 (number), 200. It is the sum of the Euler's totient function, totient function for the first twelve integers. 46 is the largest even integer that cannot be expressed as a sum of two abundant numbers. It is also the sixteenth semiprime. Since it is pos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
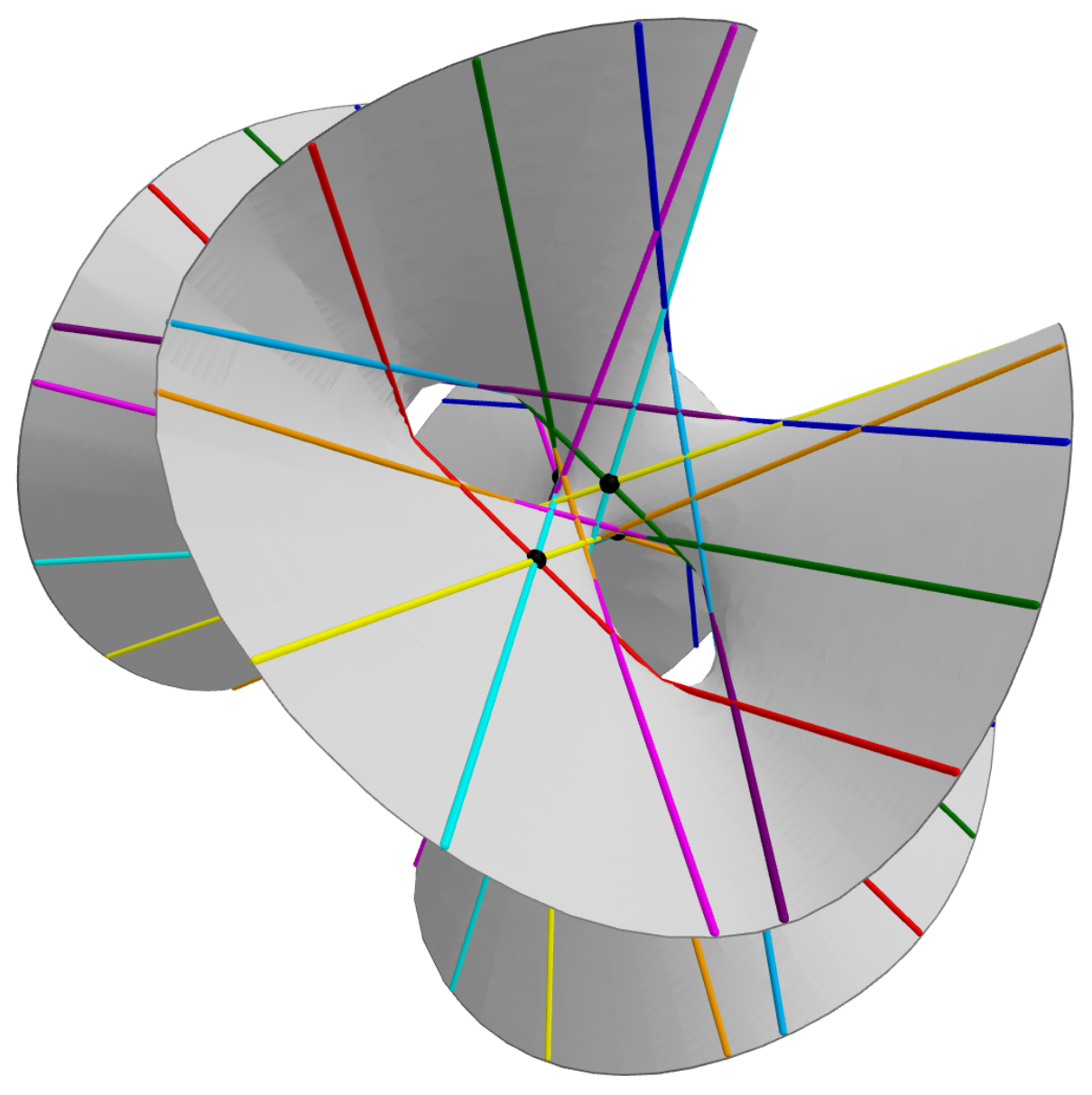
27 (number)
27 (twenty-seven) is the natural number following 26 (number), 26 and preceding 28 (number), 28. Mathematics Including the null-motif, there are 27 distinct Network motif, hypergraph motifs. There are exactly 27 lines on a cubic surface, ''twenty-seven straight lines'' on a smooth cubic surface, which give a basis of the fundamental representation of E6 (mathematics), Lie algebra \mathrm . The unique simple formally real Jordan algebra, the exceptional Jordan algebra of self-adjoint Square matrix, 3 by 3 matrices of quaternions, is 27-dimensional; its automorphism group is the 52-dimensional exceptional Lie algebra \mathrm . There are twenty-seven sporadic groups, if the Tits group, ''non-strict'' group of Lie type \mathrm (with an Faithful representation, irreducible representation that is twice that of \mathrm in 104 dimensions) is included. In Robin's theorem for the Riemann hypothesis, twenty-seven integers fail to hold \sigma(n) < e^\gamma n \log \log n for va ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |